2023年浙教版数学八年级上册第三章 一元一次不等式 章末检测（B卷）

试卷更新日期：2023-08-06 类型：单元试卷

进入 出卷网 下载

一、选择题（每题3分，共30分）

  • 1. 若x+2022>y+2022， 则（ ）
    A、x+2<y+2 B、x－2<y－2 C、－2x<－2y D、2x<2y

    查看试题解析

  • 2. 不等式3(x－2)≤x＋4的非负整数解有（     ）个
    A、4 B、5 C、6 D、无数  

    查看试题解析

  • 3. 若关于x的不等式2﹣m﹣x＞0的正整数解共有3个，则m的取值范围是（    ）
    A、﹣1≤m＜0 B、﹣1＜m≤0 C、﹣2≤m＜﹣1 D、﹣2＜m≤﹣1

    查看试题解析

  • 4. 斑马线前“车让人”，反映了城市的文明程度，但行人一般都会在红灯亮起前通过马路，某人行横道全长24米，小明以1.2m/s的速度过该人行横道，行至 13 处时，9秒倒计时灯亮了，小明要在红灯亮起前通过马路，他的速度至少要提高到原来的（   ）
    A、1.1倍 B、1.4倍 C、1.5倍 D、1.6倍

    查看试题解析

  • 5. 若关于x的一元一次不等式组{3x−2≥2(x+2)a−2x<−5的解集为x≥6 ， 且关于y的分式方程y+2ay−1+3y−81−y=2的解是正整数，则所有满足条件的整数a的值之和是（   ）
    A、5 B、8 C、12 D、15

    查看试题解析

  • 6. 关于x的不等式组 { x − 1 2 − x + 2 3 ⩽ 1 x − a > 2 只有3个整数解，求a的取值范围（   ）
    A、8＜a＜9 B、8≤a≤9 C、8≤a＜9 D、8＜a≤9

    查看试题解析

  • 7. 红星商店计划用不超过4200元的资金，购进甲、乙两种单价分别为60元、100元的商品共50件，据市场行情，销售甲、乙商品各一件分别可获利10元、20元，两种商品均售完.若所获利润大于750元，则该店进货方案有（ ）
    A、3种 B、4种 C、5种 D、6种

    查看试题解析

  • 8. 检测游泳池的水质，要求三次检验的pH的平均值不小于7.2，且不大于7.8.前两次检验，pH的读数分别是7.4，7.9，那么第三次检验的pH应该为多少才能合格?设第3次的pH值为x，由题意可得（ ）
    A、7.2×3≤7.4+7.9+x≤7.8×3 B、7.2×3< 7.4+7.9+x≤7.8×3 C、7.2×3 >7.4+7.9+x>7.8×3 D、7.2×3< 7.4+7.9+x< 7.8×

    查看试题解析

  • 9. 设a ， b是任意两个实数，用max｛a ， b｝表示a ， b两数中的较大者，例如max｛4，3｝=4，则max｛12x+4 ， x+1 ， −x+1｝的最小值等于（    ）
    A、-2 B、1 C、7 D、3

    查看试题解析

  • 10. 研究表明，运动时将心率p（次）控制在最佳燃脂心率范围内，能起到燃烧脂肪并且保护心脏功能的作用.最佳燃脂心率最高值不应该超过（220-年龄）×0.8，最低值不低于（220-年龄）×0.6.以30岁为例计算，220−30=190 ， 190×0.8=152 ， 190×0.6=114 ， 所以30岁的年龄最佳燃脂心率的范围用不等式可表示为（ ）
    A、114≤P≤152 B、144<p<152 C、114≤p≤190 D、114<p<190

    查看试题解析

二、填空题（每空3分，共18分）

  • 11. 下列命题中：

    ①若 a>b ，则 a−b<0 ；

    ②若 a<0 ，则 b−a>b ；

    ③若 a>b ，则 bc2<ac2(c≠0) ；

    ④若 ax>−a ，则 x>−1 ．

    正确的有 ． （只填写正确命题的序号）

    查看试题解析

  • 12. 如果关于 x 的不等式 (a+2021)x>a+2021  的解集为 x<1  ，那么 a 的取值范围是.

    查看试题解析

  • 13. 定义：用符号 [ m ] 表示一个实数 m 的整数部分，例如： [ 1.5 ] = 1 ， [ 0.25 ] = 0 ， [ π ] = 3 .按此定义，计算 [ 8 − 19 ] = .

    查看试题解析

  • 14. 一次测验共出5道题，做对一题得一分，已知26人的平均分不少于 4.8 分，最低的得3分，至少有3人得4分，则得5分的有 人 .

    查看试题解析

  • 15. 运行程序如图所示，规定：从“输入一个值x”到“结果是否>94”为一次程序操作，如果程序操作进行了三次才停止，那么x的取值范围是.

    查看试题解析

  • 16. 如图，用图1中的a张长方形和b张正方形纸板作侧面和底面，做成如图2的竖式和横式两种无盖纸盒，若a+b的值在285和315之间（不含285与315），且用完这些纸板做竖式纸盒比横式纸盒多30个，则a的值可能是 .

    查看试题解析

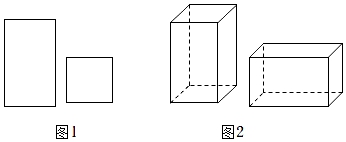
三、解答题（共9题，共66分）

  • 17. 解一元一次不等式组{3x≤2x +3x+16−1<2x+23 ， 并把解表示在数轴上．

    查看试题解析

  • 18. 已知：关于x ， y的方程组{x−y=2m+7①x+y=4m−3②的解为负数，求m的取值范围．

    查看试题解析

  • 19. 已知关于 x，y 的二元一次方程组{3x−4y=k2x−3y=2k+3 的解满足x−y<0.
    (1)、求 k 的取值范围；
    (2)、在 (1) 的条件下，若不等式(2k+ 1)x− 2k< 1的解为x>1 ， 请写出符合条件的 k 的整数值.

    查看试题解析

  • 20. 已知关于x、y的方程组 {2x−y=−1x+2y=5a−8 的解都为非负数．
    (1)、求a的取值范围；
    (2)、已知2a﹣b＝1，求a+b的取值范围；
    (3)、已知a﹣b＝m（m是大于1的常数），且b≤1，求2a+b最大值．（用含m的代数式表示）


    查看试题解析

  • 21. 根据以下素材，探索完成任务

    如何运输最省?

    素材一

    为做到“动态清零”，市卫生防疫部门需运输一批疫苗到某县，现有冷链车A 和 B型两种运输车，其中A型冷链运输车一次可运输200盒疫苗，B型冷链运输车一次可运输150盒疫苗.

    素材二

    A型冷链运输车一次需费用5000元，B型冷链运输车一次需费用3000元.

    问题解决

    任务1

    若某县需要1500盒疫苗，市卫生防疫部门只安排A型冷链运输车，则至少需A型冷链运输车多少辆？

    任务2

    市卫生防疫部门用上述两种冷冻车共12辆运输这批疫苗.若运输疫苗不少于2100盒，且总费用小于54000元请你列出所有的运输方案.

    任务3

    在任务2的条件下，由于A型和 B型两种运输车，运输时走不同高速路线，A型需a元过路费， B型（100-a）元过路费，求如何安排两种车型运输的过路费总和最少？

    查看试题解析

  • 22. 在抗击新冠肺炎疫情期间，市场上防护口罩出现热销，某药店出售一批口罩．已知3包儿童口罩和2包成人口罩共26个，5包儿童口罩和3包成人口罩共40个．
    (1)、求儿童口罩和成人口罩的每包各是多少个？
    (2)、某家庭欲购进这两种型号的口罩共5包，为使其中口罩总数量不低于18个，且不超过34个：

    ①有哪几种购买方案？

    ②若每包儿童口罩8元，每包成人口罩25元，哪种方案总费用最少？

    查看试题解析

  • 23. 随着新冠疫情的出现，口罩成为日常生活的必需品，某医药公司每月生产甲、乙两种型号的防疫口罩共20万只，且所有口罩当月全部卖出，其中成本、售价如表：

    甲

    乙

    成本

    12元/只

    4元/只

    售价

    18元/只

    6元/只
    (1)、若该公司三月份的利润为100万元，求生产甲、乙两种型号的防疫口罩分别是多少万只？（利润＝售价-成本）
    (2)、如果该公司四月份投入成本不超过216万元，该医药公司四月份最多只能生产甲种防疫口罩多少万只？
    (3)、某学校到该公司购买乙型口罩有如下两种方案，方案一：乙型口罩一律打9折：方案二：购买168元会员卡后，乙型口罩一律8折，请帮学校设计出合适的购买方案.

    查看试题解析

  • 24. 参加学校运动会，八年级1班第一天购买了水果，面包，饮料，药品等四种食品，四种食品购买金额的统计图表如图1、图2所示，若将水果、面包、药品三种食品统称为非饮料食品，并规定t=饮料金额：非饮料金额．

    (1)、①求t的值；

    ②求扇形统计图中钝角∠AOB的度数

    (2)、根据实际需要，该班第二天购买这四种食品时，增加购买饮料金额，同时减少购买面包金额假设增加购买饮料金额的25%等于减少购买面包的金额，且购买面包的金额不少于100元，求t的取值范围

    查看试题解析

  • 25. 某工厂用如图甲所示的长方形和正方形纸板，做成如图乙所示的竖式与横式两种长方体形状的无盖的纸盒．

    (1)、现有正方形纸板162张，长方形纸板340张，若要做两种纸盒共100个，设竖式纸盒x个，需要长方形纸板张，正方形纸板张（请用含有x的式子）
    (2)、在（1）的条件下，有哪几种生产方案？
    (3)、若有正方形纸板162张，长方形纸板a张，做成上述两种纸盒，纸板恰好用完．已知290＜a＜300，求a的值．

    查看试题解析