2023-2024学年高中数学人教A版选择性必修一 1.3 空间向量的运算坐标表示 同步练习
试卷更新日期:2023-08-06 类型:同步测试
一、选择题
-
1. 已知空间向量 , 则( )A、 B、 C、 D、2. 已知空间向量 , , , 若 , 则( )A、2 B、-2 C、14 D、-143. 已知空间向量 , , 则( )A、 B、6 C、36 D、404. 已知三点,且 , 则实数的值为( )A、-2 B、-1 C、1 D、25. 设 , , 与垂直,则等于( )A、6 B、14 C、-14 D、-66. 如图,平行六面体中,为的中点.若 , 则( )
 A、 B、 C、 D、7. 已知则( )A、2 B、 C、1 D、08. 如图,直角梯形 , , , , 是边中点,沿翻折成四棱锥 , 则点到平面距离的最大值为( )
A、 B、 C、 D、7. 已知则( )A、2 B、 C、1 D、08. 如图,直角梯形 , , , , 是边中点,沿翻折成四棱锥 , 则点到平面距离的最大值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、多项选择题
-
9. 已知向量 , , , 则( )A、 B、 C、 D、10. 在空间直角坐标系中,已知向量 , .以下各组值中能使得的是( )A、 , B、 , C、 , D、 ,11. 如图,在三棱锥中,平面 , , , , 以B为原点,分别以 , , 的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,设平面PAB和平面PBC的一个法向量分别为 , , 则下列结论中正确的是()
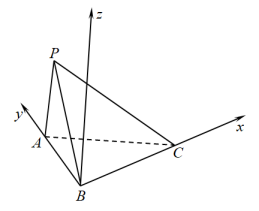 A、点P的坐标为 B、 C、 D、12. 已知向量 , 则( )A、 B、 C、 D、与的夹角为13. 如图,已知正方体的棱长为 , 、分别为棱、的中点,则下列结论正确的为( )
A、点P的坐标为 B、 C、 D、12. 已知向量 , 则( )A、 B、 C、 D、与的夹角为13. 如图,已知正方体的棱长为 , 、分别为棱、的中点,则下列结论正确的为( ) A、 B、 C、 D、为平面的一个法向量14. 如图,在直三棱柱中, , , , 为棱的中点;为棱上的动点(含端点),过点A、、作三棱柱的截面 , 且交于 , 则( )
A、 B、 C、 D、为平面的一个法向量14. 如图,在直三棱柱中, , , , 为棱的中点;为棱上的动点(含端点),过点A、、作三棱柱的截面 , 且交于 , 则( ) A、线段的最小值为 B、棱上的不存在点 , 使得平面 C、棱上的存在点 , 使得 D、当为棱的中点时,
A、线段的最小值为 B、棱上的不存在点 , 使得平面 C、棱上的存在点 , 使得 D、当为棱的中点时,三、填空题
-
15. 已知 , , 若 , 则 .16. 已知 , 则 .17. 已知 , , , 则以 , 为邻边的平行四边形的面积是.18. 已知向量 , , . 若 , 则 .19. 已知向量 , , 若 , 则 .20. 已知 , ,若 ,则 的取值范围为 .
四、解答题
-
21. 已知 , , .(1)、若四边形 为平行四边形,求实数 , 的值;(2)、若四边形 的对角线互相垂直,求实数 , 满足的关系式.22. 如图,建立空间直角坐标系 .单位正方体 顶点A位于坐标原点,其中点 ,点 ,点 .
 (1)、若点E是棱 的中点,点F是棱 的中点,点G是侧面 的中心,则分别求出向量 的坐标;(2)、在(1)的条件下,分别求出 , 的值.
(1)、若点E是棱 的中点,点F是棱 的中点,点G是侧面 的中心,则分别求出向量 的坐标;(2)、在(1)的条件下,分别求出 , 的值.
