2023年浙教版数学八年级上册第三章一元一次不等式章末检测（A卷）

试卷更新日期：2023-08-06 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 在下列数学表达式：① $- 2 < 0$ ， ② $2 y - 5 > 1$ ， ③ $m = 1$ ， ④ $x^{2} - x$ ， ⑤ $x + 1 < 2 x - 1$ 中，是不等式的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下列不等式中，一元一次不等式有（）
① $x^{2} + 3 > 2 x$ ② $\frac{1}{x} - 3 > 0$ ③ $x - 3 > 2 y$
④ $\frac{x - 1}{π} \geq 5 π$ ⑤ $3 y > - 3$

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
3.
下面给出的不等式组中
其中是一元一次不等式组的个数是（　　）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 已知 $a < b$ ，则下列式子中错误的是（）

A、 $a - 1 < b - 1$ B、 $a + 2 < b + 2$ C、 $- 4 a < - 4 b$ D、 $\frac{a}{3} < \frac{b}{3}$

查看试题解析
5. 若 $m > n$ ，下列不等式不一定成立的是（）

A、 $m + 3 > n + 3$ B、 $5 m > 5 n$ C、 $\frac{m}{6} > \frac{n}{6}$ D、 $m^{2} > n^{2}$

查看试题解析
6. 不等式 $x - 3 > 0$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
7. 不等式组 ${\begin{cases} 2 (x - 1) > x - 3 \\ 3 x \geq 5 x - 2 \end{cases}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
8. 已知关于 $x$ 的不等式 $4 x > a$ 的负整数解是 $- 1$ 和 $- 2$ ，则 $a$ 的取值范围（）

A、 $- 12 < a < - 8$ B、 $- 12 \leq a < - 8$ C、 $- 12 < a \leq - 8$ D、 $- 12 \leq a \leq - 8$

查看试题解析
9. 一次智力测试有20道选择题．该测试题的评分标准是：答对1题得5分，答错1题扣2分，不答题得0分．小明有2道题未答，要使总分不低于60分，答对的题数至少是（）

A、12 B、13 C、14 D、15

查看试题解析
10. 八年级某班级部分同学去植树，若每人平均植树7棵，还剩9棵，若每人平均植树9棵，则有1名同学植树的棵数不到8棵若设同学人数为x人，下列各项能准确的求出同学人数与种植的树木的数量的是 $($ $)$

A、 $7 x + 9 - 9 (x - 1) > 0$ B、 $7 x + 9 - 9 (x - 1) < 8$ C、 ${\begin{array}{l} 7 x + 9 - 9 (x - 1) \geq 0 \\ 7 x + 9 - 9 (x - 1) < 8 \end{array}$ D、 ${\begin{array}{l} 7 x + 9 - 9 (x - 1) \geq 0 \\ 7 x + 9 - 9 (x - 1) \leq 8 \end{array}$

查看试题解析

二、填空题（每空3分，共21分）

11. 若不等式 $(a - 3) x > a - 3$ 可以变形为 $x < 1$ ，则a的取值范围是．

查看试题解析
12. 若 $a < b$ ，则 $- \frac{1}{2} a$ $- \frac{1}{2} b$ （填不等号）

查看试题解析
13. 不等式 $\frac{3 x - 1}{5} - \frac{x - 1}{2} \geq 1$ 的最小整数解是．

查看试题解析
14. 在今年6.18网购狂欢节上，某网店商家对一电子产品进行打折促销，已知它的进价为800元，标价为1100元，商家为了保证利润率不低于 $10 %$ ，则至多可打折．

查看试题解析
15. 人教版七年级下册数学课本共有如下6章内容：《相交线与平行线》、《实数》、《平面直角坐标系》、《二元一次方程组》、《不等式与不等式组》、《数据的收集、整理与描述》．若某期末试卷要求，每章至少有4个题，全卷总题数不超过26个题，设本期末试卷的全卷总题数为x个题，则x的取值范围是．

查看试题解析
16. 如图，某同学设计了一种计算流程图，据图完成下列问题：

(1)、任意写出一个实数，使得该值经过一次运行就能输出结果，则该数为．

(2)、如果要使开始输入的x的值经过两次运行才能输出结果，那么x的整数值为．

查看试题解析

三、解答题（共10题，共69分）

17. 解不等式：

(1)、 $5 x - 3 < 1 + 3 x$ ；

(2)、 $\frac{1 + x}{2} \leq \frac{1 + 2 x}{3} + 1$ .

查看试题解析
18. 解不等式组： ${\begin{array}{l} x - 1 < 2 \\ 3 (x + 1) \geq 2 x + 2 \end{array}$ ，并把它的解集在数轴上表示出来．

查看试题解析
19.

(1)、若x＞y，比较﹣3x+5与﹣3y+5的大小，并说明理由；

(2)、若x＞y，且（a﹣3）x＜（a﹣3）y，求a的取值范围．

查看试题解析
20. x取哪些整数时，不等式 $2 x - 1 > - 3$ 与 $\frac{1 + 2 x}{3} \geq x - 1$ 都成立？

查看试题解析
21. 对于任意数a、b，定义关于“※”的一种运算如下： $a ※ b = 2 a - b$ ．例如： $5 ※ 2 = 2 \times 5 - 2 = 8$ ．若 $(x + 2) ※ 3 < 6 ※ x$ ，求x的非负整数解的和．

查看试题解析
22. 下面是小明解不等式 $\frac{x + 5}{2} - 1 < \frac{3 x + 2}{2}$ 的过程：
解：去分母，得：x+5-1<3x+2；…………………………………………第一步

移项、合并同类项，得：-2x<-2；…………………………………………第二步

系数化为1，得：x>1…………………………………………第三步.

(1)、小明是从第步开始出错的，错误的原因是；

(2)、第三步“系数化为1”的依据是；

(3)、请你给出正确的解答过程，并把此不等式的解集在数轴上表示出来.

查看试题解析
23. 解不等式组： ${\begin{array}{l} － 2 x \leq 6 ① \\ x ＞－ 2 ② \\ 3 (x － 1) ＜ x + 1 ③ \end{array}$
请结合题意，完成本题的解答.

(1)、解不等式①，得，依据是：；

(2)、解不等式③，得；

(3)、把不等式①，②和③的解集在数轴上表示出来：

(4)、从图中可以找出三个不等式解集的公共部分，得不等式组的解集为.

查看试题解析
24. 某市为了提高市民的交通安全意识，要求骑行过程中必须佩戴安全头盔，可以保护头部，减少伤害．某商店经销甲、乙两种安全头盔，进价、售价见下表．

甲

乙

进价（元/顶）

40

30

售价（元/顶）

60

m

(1)、若该商店进货甲、乙两种安全头盔共100顶，一共花费了3700元，求甲、乙两种安全头盔分别进货多少顶？

(2)、在（1）的条件下，将头盔全部售出，商家把乙种安全头盔的售价m至少定为多少元，才能保证利润不低于1700元？

查看试题解析
25. 如图，“开心”农场准备用 $50 m$ 的护栏围成一块靠墙的长方形花园，设长方形花园的长为 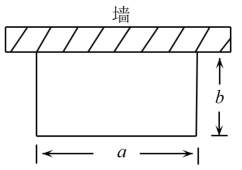$a m$ ，宽为 $b m$ ．

(1)、写出用b表示a的式子a= ．当 $a = 20$ 时，求b的值；

(2)、受场地条件的限制，a的取值范围为 $18 \leq a \leq 26$ ，求b的取值范围．

查看试题解析
26. “新冠疫情”对全球经济造成了严重冲击，英雄的武汉人民为抗击“疫情”付出了巨大的努力并取得了伟大的胜利．为了加快复工复产，武汉市某企业需要运输一批生产物资．根据调查得知，2辆大货车与3辆小货车一次可以运输600箱生产物资；5辆大货车与6辆小货车一次可以运输1350箱生产物资．

(1)、求1辆大货车和1辆小货车一次分别可以运输多少箱生产物资？

(2)、现计划用这样的两种货车共12辆运输这批生产物资，已知每辆大货车一次需要运输费用5000元，每辆小货车一次需要运输费用3000元．若运输物资不少于1500箱，并且运输总费用小于54000元，请你列出所有运输方案，并指出哪种运输方案所需费用最少，最少费用是多少元？

查看试题解析

	甲	乙
进价（元/顶）	40	30
售价（元/顶）	60	m

2023年浙教版数学八年级上册第三章 一元一次不等式 章末检测（A卷）

一、选择题（每题3分，共30分）

二、填空题（每空3分，共21分）

三、解答题（共10题，共69分）

2023年浙教版数学八年级上册第三章一元一次不等式章末检测（A卷）