2023年浙教版数学八年级上册3.4 一元一次不等式组 同步测试(提高版)
试卷更新日期:2023-08-06 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 不等式组的解集表示在数轴上正确的是( )A、
 B、
B、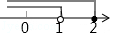 C、
C、 D、
D、 2. 若关于x的不等式组的整数解共有3个,则m的取值范围是( )A、5<m<6 B、5<m≤6 C、5≤m≤6 D、6<m≤73. 若关于x的不等式组 有四个整数解,则a的取值范围是( )A、- < a≤ - B、- ≤a < - C、- ≤a≤ - D、- < a < -4. 若不等式组的解集为1<x<2,则(m+n)2022的值为( )A、-1 B、0 C、1 D、25. 对于任意实数p、q,定义一种运算: , 如: , 请根据以上定义解决问题:若关于x的不等式组 有2个整数解,则m的取值范围为是( )A、3≤m<5 B、3<m≤5 C、3≤m≤5 D、3<m<56. 如图是测量一颗玻璃球体积的过程:
2. 若关于x的不等式组的整数解共有3个,则m的取值范围是( )A、5<m<6 B、5<m≤6 C、5≤m≤6 D、6<m≤73. 若关于x的不等式组 有四个整数解,则a的取值范围是( )A、- < a≤ - B、- ≤a < - C、- ≤a≤ - D、- < a < -4. 若不等式组的解集为1<x<2,则(m+n)2022的值为( )A、-1 B、0 C、1 D、25. 对于任意实数p、q,定义一种运算: , 如: , 请根据以上定义解决问题:若关于x的不等式组 有2个整数解,则m的取值范围为是( )A、3≤m<5 B、3<m≤5 C、3≤m≤5 D、3<m<56. 如图是测量一颗玻璃球体积的过程:
(1)将的水倒进一个容量为的杯子中;
(2)将五颗相同的玻璃球放入水中,结果水没有满;
(3)再加一颗同样的玻璃球放入水中,结果水满溢出.根据以上过程,推测这样一颗玻璃球的体积范围是( )
A、以上,以下 B、以上,以下 C、以上,以下 D、以上,以下7. 对一实数x按如图所示程序进行操作,规定:程序运行从“输入一个实数x”到“判断结果是否大于190?”为一次操作,如果操作恰好进行两次后停止,则x的取值范围是( ) A、x<64 B、x>22 C、22<x≤64 D、22<x<648. 对于任意实数p、q,定义一种运算:p@q=p-q+pq,例如2@3=2-3+2×3.请根据上述定义解决问题:若关于x的不等式组有3个整数解,则m的取值范围为是 ( )A、-8≤m<-5 B、-8<m≤-5 C、-8≤m≤-5 D、-8<m<-59. 某商店甲商品的单价为8元,乙商品的单价为2元.已知购买乙商品的件数比购买甲商品的件数的2倍少4件,如果购买甲、乙两种商品的总件数不少于32,且购买甲、乙两种商品的总费用不超过148元.设购买甲商品x件,依题意可列不等式组得( )A、 B、 C、 D、10. 某电脑用户计划使用不超过530元的资金购买单价为70元的单片软件和80元的盒装磁带,根据需要,软件至少买3片,磁盘至少买2盒,那么不相同的购买方式共有( )A、4 种 B、5 种 C、6 种 D、7 种
A、x<64 B、x>22 C、22<x≤64 D、22<x<648. 对于任意实数p、q,定义一种运算:p@q=p-q+pq,例如2@3=2-3+2×3.请根据上述定义解决问题:若关于x的不等式组有3个整数解,则m的取值范围为是 ( )A、-8≤m<-5 B、-8<m≤-5 C、-8≤m≤-5 D、-8<m<-59. 某商店甲商品的单价为8元,乙商品的单价为2元.已知购买乙商品的件数比购买甲商品的件数的2倍少4件,如果购买甲、乙两种商品的总件数不少于32,且购买甲、乙两种商品的总费用不超过148元.设购买甲商品x件,依题意可列不等式组得( )A、 B、 C、 D、10. 某电脑用户计划使用不超过530元的资金购买单价为70元的单片软件和80元的盒装磁带,根据需要,软件至少买3片,磁盘至少买2盒,那么不相同的购买方式共有( )A、4 种 B、5 种 C、6 种 D、7 种二、填空题(每空4分,共24分)
-
11. 若关于x的不等式组有且仅有一个整数解 , 则实数a的取值范围是.12. 若关于x的一元一次不等式组无解,则a的取值范围是。13. 如果关于x的不等式组 的整数解只有1,2,3,那么a的取值范围是 , b的取值范围是.14. 若关于x的不等式组无解,且关于y的分式方程的解为非负整数,则符合条件的所有整数a的和为 .15. 已知n为整数,若一个三角形的三边长分别是 , ,6n , 则所有满足条件的n值的和为 .16. 如图, , 现用若干根等长的小棒从点A开始向右依次摆放,使小棒的两端恰好分别落在射线OB、OC上,其中AA1为第1根小棒,且OA=AA1. 若恰好能摆放4根小棒,则θ 的取值范围是 .

三、解答题(共8题,共66分)
-
17. 解下列不等式组:(1)、 ;(2)、 .18.(1)、解不等式: , 并把解集在数轴上表示出来;
 (2)、解不等式组 , 并写出它的最大整数解.19. 以下是圆圆解不等式组 的解答过程: 解:由①,得2+x>﹣2,所以x>﹣4.由②,得1﹣x>﹣3,所以﹣x>﹣2,所以x>2. 所以原不等式组的解是x>2.圆圆的解答过程是否有错误?如果有错误,请写出正确的解答过程.20. 某社区为了更好地开展“垃圾分类,美丽永州”活动,需购买A,B两种类型垃圾桶,用1600元可购进A型垃圾桶14个和B型垃圾桶8个,且购买3个A型垃圾桶的费用与购买4个B型垃圾桶的费用相同,请解答下列问题:(1)、求出A型垃圾桶和B型垃圾桶的单价.(2)、若社区欲用不超过3600元购进两种垃圾桶共50个,其中A型垃圾桶至少29个,求有哪几种购买方案?21. 为更好地推进生活垃圾分类工作,改善城市生态环境,某小区准备购买A、B两种型号的垃圾箱,通过对市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需390元,购买2个A型垃圾箱比购买1个B型垃圾箱少用20元.(1)、求每个A型垃圾箱和每个B型垃圾箱分别多少元?(2)、该小区计划用不多于1500元的资金购买A、B两种型号的垃圾箱共20个,且A型号垃圾箱个数不多于B型垃圾箱个数的3倍,则该小区购买A、B两种型号垃圾箱的方案有哪些?22. 为纪念今年建党一百周年,学校集团党委决定印制《党旗飘扬》、《党建知识》两种党建读本.已知印制《党旗飘扬》5册和《党建知识》10册,需要350元;印制《党旗飘扬》3册和《党建知识》5册,需要190元.(1)、求印制两种党建读本每册各需多少元?(2)、考虑到宣传效果和资金周转,印制《党旗飘扬》不能少于60册,且用于印制两种党建读本的资金不能超过2630元,现需要印制两种读本共100册,问有哪几种印制方案?哪种方案费用最少?23. 经销商销售甲型、乙型两种产品,价格随销售量的变化而不同,具体如表:
(2)、解不等式组 , 并写出它的最大整数解.19. 以下是圆圆解不等式组 的解答过程: 解:由①,得2+x>﹣2,所以x>﹣4.由②,得1﹣x>﹣3,所以﹣x>﹣2,所以x>2. 所以原不等式组的解是x>2.圆圆的解答过程是否有错误?如果有错误,请写出正确的解答过程.20. 某社区为了更好地开展“垃圾分类,美丽永州”活动,需购买A,B两种类型垃圾桶,用1600元可购进A型垃圾桶14个和B型垃圾桶8个,且购买3个A型垃圾桶的费用与购买4个B型垃圾桶的费用相同,请解答下列问题:(1)、求出A型垃圾桶和B型垃圾桶的单价.(2)、若社区欲用不超过3600元购进两种垃圾桶共50个,其中A型垃圾桶至少29个,求有哪几种购买方案?21. 为更好地推进生活垃圾分类工作,改善城市生态环境,某小区准备购买A、B两种型号的垃圾箱,通过对市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需390元,购买2个A型垃圾箱比购买1个B型垃圾箱少用20元.(1)、求每个A型垃圾箱和每个B型垃圾箱分别多少元?(2)、该小区计划用不多于1500元的资金购买A、B两种型号的垃圾箱共20个,且A型号垃圾箱个数不多于B型垃圾箱个数的3倍,则该小区购买A、B两种型号垃圾箱的方案有哪些?22. 为纪念今年建党一百周年,学校集团党委决定印制《党旗飘扬》、《党建知识》两种党建读本.已知印制《党旗飘扬》5册和《党建知识》10册,需要350元;印制《党旗飘扬》3册和《党建知识》5册,需要190元.(1)、求印制两种党建读本每册各需多少元?(2)、考虑到宣传效果和资金周转,印制《党旗飘扬》不能少于60册,且用于印制两种党建读本的资金不能超过2630元,现需要印制两种读本共100册,问有哪几种印制方案?哪种方案费用最少?23. 经销商销售甲型、乙型两种产品,价格随销售量的变化而不同,具体如表:销售量(件
价格(元件)
型号
甲型
乙型
已知销售10件甲型产品和30件乙型产品的销售额为750元;销售60件甲型产品和100件乙型产品的销售额为2520元.
(1)、求、的值;(2)、若学校要购买甲型、乙型两种产品共101件,购买的甲产品少于乙产品,所用经费不超过1680元,则有多少种购买方案?24. 接种新冠病毒疫苗,建立全民免疫屏障,是战胜病毒的重要手段.北京科兴中维需运输一批疫苗到我市疾控中心,据调查得知,2辆 型冷链运输车与3辆 型冷链运输车一次可以运输600盒:5辆 型冷链运输车与6辆 型冷链运输车一次可以运输1350盒.(1)、求每辆 型车和每辆 型车一次可以分别运输多少盒疫苗.(2)、计划用两种冷链运输车共12辆运输这批疫苗, 型车一次需费用5000元, 型车一次需费用3000元.若运输物资不少于1500盒,且总费用小于54000元.请你列出所有运输方案,并指出哪种方案所需费用最少,最少费用是多少?