2023-2024学年高中数学人教A版选择性必修一 1.1 空间向量及其运算 同步练习
试卷更新日期:2023-08-06 类型:同步测试
一、选择题
-
1. 在棱长为的正方体中,是的中点,则( )A、0 B、1 C、 D、22. 如图,在四面体中,点为棱的中点,设 , , , 则( )
 A、 B、 C、 D、3. 如图,向量 , , , 则向量可以表示为( )
A、 B、 C、 D、3. 如图,向量 , , , 则向量可以表示为( )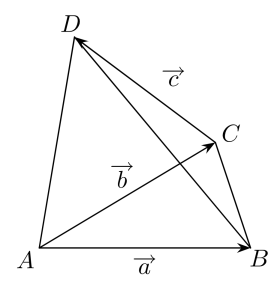 A、 B、 C、 D、4. 如图在平行六面体中,相交于 , 为的中点,设 , , , 则( )
A、 B、 C、 D、4. 如图在平行六面体中,相交于 , 为的中点,设 , , , 则( ) A、 B、 C、 D、5. 如图,空间四边形中, , , .点在上,且 , 为的中点,则( )
A、 B、 C、 D、5. 如图,空间四边形中, , , .点在上,且 , 为的中点,则( )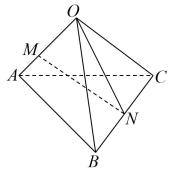 A、 B、 C、 D、6. 点是棱长为1的正方体的底面上一点,则的取值范围是( )A、 B、 C、 D、7. 《九章算术》中的“商功”篇主要讲述了以立体几何为主的各种形体体积的计算,其中堑堵是指底面为直角三角形的直棱柱.如图,在堑堵中,分别是的中点,是的中点,若 , 则( )
A、 B、 C、 D、6. 点是棱长为1的正方体的底面上一点,则的取值范围是( )A、 B、 C、 D、7. 《九章算术》中的“商功”篇主要讲述了以立体几何为主的各种形体体积的计算,其中堑堵是指底面为直角三角形的直棱柱.如图,在堑堵中,分别是的中点,是的中点,若 , 则( ) A、1 B、 C、 D、8. 如图,四面体的所有棱长都相等, , , 则( )
A、1 B、 C、 D、8. 如图,四面体的所有棱长都相等, , , 则( ) A、 B、 C、 D、9. 如图所示,在平行六面体中,E,F,H分别为 , , DE的中点.若 , , , 则向量可用表示为( )
A、 B、 C、 D、9. 如图所示,在平行六面体中,E,F,H分别为 , , DE的中点.若 , , , 则向量可用表示为( )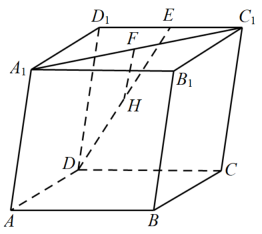 A、 B、 C、 D、10. 下列关于空间向量的说法中错误的是( )A、零向量与任意向量平行 B、任意两个空间向量一定共面 C、零向量是任意向量的方向向量 D、方向相同且模相等的两个向量是相等向量
A、 B、 C、 D、10. 下列关于空间向量的说法中错误的是( )A、零向量与任意向量平行 B、任意两个空间向量一定共面 C、零向量是任意向量的方向向量 D、方向相同且模相等的两个向量是相等向量二、多项选择题
-
11. 设动点 在正方体 的对角线 上,记 当 为钝角时,则实数可能的取值是( )A、 B、 C、 D、112. 设 , 为空间中的任意两个非零向量,下列各式中正确的有( ).A、 B、 C、 D、13. 判断下列结论正确的是( )A、空间中任意两个非零向量 , 共面. B、在三个向量的数量积运算中 . C、对于非零向量 ,由数量积 ,则 . D、若 , , , 是空间任意四点,则有 .14. 下列命题正确的是( )A、零向量与任意向量平行 B、是向量的必要不充分条件 C、向量与向量是共线向量,则点 , , , 必在同一条直线上 D、空间中任意两个向量 , , 则一定成立15. 在棱长均为1的四面体中,下列结论正确的是( )A、 B、 C、 D、16. 给出下列命题,其中正确的命题是( )A、若 ,则 或 B、若向量 是向量 的相反向量,则 C、在正方体 中, D、若空间向量 , , 满足 , ,则
三、填空题
-
17. 在直三棱柱中,若 , 则=.(用表示)18. 已知 、 、 、 为空间中任意四点,化简 .19. 对于空间中的非零向量 , , ,有下列各式:
① ;
② ;
③ ;
④ .
其中一定不成立的是(填序号).
20. 若、、是棱长为的正四面体棱上互不相同的三点,则的取值范围是.21. 正方体 ABCD-A1B1C1D1 的棱长为1,若动点p在线段 上运动, 则 的取值范围是 .22. 在棱长为a的正方体 中,向量 与向量 所成的角为.四、解答题
-
23. 如图,在平行六面体 中, , .

求:(Ⅰ) ;
(Ⅱ) 的长.
24. 如图,点M,N分别在对角线 上,且 .求证:向量 共面. 25. 如图,在四棱锥中,底面是平行四边形,Q为的中点.
25. 如图,在四棱锥中,底面是平行四边形,Q为的中点. (1)、用 , , 表示;(2)、若底面是正方形,且 , , 求.
(1)、用 , , 表示;(2)、若底面是正方形,且 , , 求.