2023年浙教版数学八年级上册第二章 特殊三角形 章末检测（B卷）
试卷更新日期：2023-08-06 类型：单元试卷
一、选择题（每题3分，共30分）
-
1. 在平面直角坐标系中，横、纵坐标都是整数的点叫做格点．如图，点A的坐标为 ， 点B的坐标为 ， 点C为第一象限内的格点，若不共线的A，B，C三点构成轴对称图形，则满足条件的点C的个数为（ ）
A、2 B、4 C、6 D、82. 如图.在五边形ABCDE中，∠BAE＝136°，∠B＝∠E＝90°，在BC、DE上分别找一点M、N，使得△AMN的周长最小时，则∠AMN＋∠ANM的度数为（ ）
A、84° B、88° C、90° D、96°3. 如图，四边形ABCD中，AB＝AD，点B关于AC的对称点B′ 恰好落在CD上，若∠BAD＝110°，则∠ACB的度数为（ ）
A、40° B、35° C、60° D、70°4. 如图，直线a，b相交形成的夹角中，锐角为52°，交点为O，点A在直线a上，直线b上存在点B，使以点O，A，B为顶点的三角形是等腰三角形，这样的点B有（ ）
A、1个 B、2个 C、3个 D、4个5. 如图，在△ABC中，∠BAC＝90°，AD是高，BE是中线，CF是角平分线，CF交AD于点G，交BE于点H．下列结论：①S△ABE＝S△BCE；②∠AFG＝∠AGF；③BH＝CH；④∠FAG＝2∠ACF，其中正确的是（ ）
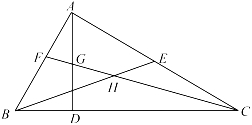A、①②③ B、①②④ C、①③④ D、②③④6. 如图，已知在Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，F是BC边上的中点.若动点E从A点出发以2cm/s的速度沿着A→B→A方向运动，设运动时间为t(s)(0≤t＜3)，连结EF.当△BEF是直角三角形时，t的值为（ ）.
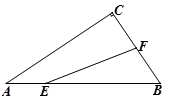A、 B、1 C、 或1或 D、 或1或7. 如图，在长方体透明容器（无盖）内的点 处有一滴糖浆，容器外 点处的蚂蚁想沿容器壁爬到容器内吃糖浆，已知容器长为 ，宽为 ，高为 ，点 距底部 ，请问蚂蚁需爬行的最短距离是（容器壁厚度不计）（ ）
A、 B、 C、 D、8. 如图，在等腰△ABC与等腰△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=α，连接BD和CE相交于点P，交AC于点M，交AD与点N.下列结论：①BD=CE；②∠BPE=180°−2α；③AP平分∠BPE；④若α=60°，则PE=AP+PD.其中一定正确的结论的个数是（ ）
A、1 B、2 C、3 D、49. 如图，在平面直角坐标系中，点A的坐标为（4，0），点Q是直线yx上的一个动点，以AQ为边，在AQ的右侧作等边△APQ，使得点P落在第一象限，连接OP，则OP+AP的最小值为（ ）
A、6 B、4 C、8 D、610. 在△ABC中，∠BAC=90°，点D在边BC上，AD=AB （ ）
A、若AC=2AB，则∠C=30° B、若AC=2AB，则3BD=2CD C、若∠B=2∠C，则AC=2AB D、若∠B=2∠C，则S△ABD=2△ACD二、填空题（每空3分，共21分）
-
11. 下列命题中，逆命题是真命题的是（只填写序号）。
①直角三角形两条直角边的平方和等于斜边的平方；
②等腰三角形两腰的高线相等；
③若三条线段a，b，c是三角形的三边，则这三条线段满足a+b>c
④角的内部，到角两边距离相等的点在这个角的平分线上，
⑤全等三角形的面积相等；
12. 已知，在△ABC中，∠A＝48°，过△ABC的某个顶点的直线把原三角形分成两个等腰三角形，则△ABC中最小的角为.13. 如图， ， ， AD是∠BAC内的一条射线，且 ， P为AD上一动点，则的最大值是 ．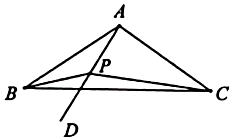
14. 如图，在△ABC中，AB=AC，D、E是△ABC内两点，AD平分∠BAC，∠EBC=∠E=60°，若BE=30cm，DE=2cm，则BC=cm.
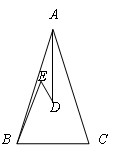15. 如图，在等腰三角形ABC中，AB＝AC，∠B＝50°，D为BC的中点，点E在AB上，∠AED＝70°，若点P是等腰三角形ABC的腰上的一点，则当 是以∠EDP为顶角的等腰三角形时，∠EDP的度数是.
16. 如图：在△ABC中，∠C=90°，BC=6cm，AC=8cm，BD是∠ABC的角平分线。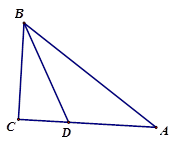
(1)、则CD=；(2)、若点E是线段AB上的一个动点，从点B以每秒1cm的速度向A运动， 秒种后△EAD是直角三角形三、作图题（共8分）
-
17. 如图所示，在平面直角坐标系中 的三个顶点坐标分别为 ， ， ．
(1)、作出 关于x轴对称的 ；(2)、 的面积为 ， 边上的高为；(3)、在y轴找一点P，使得 的周长最小，请画出点P，并直接写出 的周长最小值为；(4)、在x轴上找一点P，使得 为等腰三角形，则点P的坐标为 ．四、解答题（共7题，共61分）
-
18. 图1、图2、图3均是5×5的正方形网格，每个小正方形的边长均为1，其顶点称为格点，的顶点均在格点上．只用无刻度的直尺，在给定的网格中，按下列要求作图，保留作图痕迹．
(1)、网格中的形状是；(2)、在图1中确定一点D，连接 ， 使与全等但不成轴对称；(3)、在图2中确定一点D，连接 ， 使与成轴对称；(4)、在图3中边上找一个点D，使得它与点与点构成的三角形为等腰三角形．19. 勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”（如图①），后人称之为“赵爽弦图”，流传至今.如图①是用四个能够完全重合的直角三角形拼成的图形，其中直角边长分别为a，b，斜边长为c，用含a，b，c的代数式表示：
(1)、大正方形的面积为；小正方形的面积为；(2)、四个直角三角形的面积和为 ， 根据图中面积关系，可列出a，b，c之间的关系式为；(3)、如图②，以直角三角形的三边为直径，分别向外部作半圆，则 ， ， 满足的关系是；(4)、如图③直角三角形的两条直角边长分别为3、5，分别以直角三角形的三边为直径作半圆，则图中两个月形图案（阴影部分）的面积和为.20. 两个顶角相等的等腰三角形，如果具有公共的顶角顶点，并将它们的底角顶点分别对应连接起来得到两个全等三角形，我们把这样的图形称为“手拉手”图形．如图1，在“手拉手”图形中，AB＝AC，AD＝AE，∠BAC＝∠DAE，连结BD，CE，则△ABD≌△ACE．
(1)、请证明图1的结论成立；(2)、如图2，△ABC和△AED是等边三角形，连接BD，EC交于点O，求∠BOC的度数；(3)、如图3，AB＝BC，∠ABC＝∠BDC＝60°，试探究∠A与∠C的数量关系．21. 如图1、在△ABC中，E、D是BC边上的点，且AE是∠BAD的平分线，∠CAE+∠BEA=180°
(1)、若∠CAD=25°，∠C=38°，求∠DAE的度数(2)、当BE=AC时，请猜想线段AB、AD之间的数量关系；并证明你的猜想.(3)、如图2，在（2）的条件下，过D作DF⊥AE，垂足为F，交AB于G，如果 ， 请直接写出四边形AFDC的面积.22. 在中， ， 是射线上的一点，过点分别作于点 ， 于点 ．
(1)、如图1，若是边上的中点，求证： ．(2)、过点作于点 ．①如图2，若是边上的任意一点，求证：；
②若点是射线上一点， ， ， ， 求的长度．
23.
(1)、阅读理解：问题：如图1，在四边形 中，对角线 平分 ， .求证： .思考：“角平分线+对角互补”可以通过“截长、补短”等构造全等去解决问题.
方法1：在 上截取 ，连接 ，得到全等三角形，进而解决问题；
方法2：延长 到点N，使得 ，连接 ，得到全等三角形，进而解决问题.
结合图1，在方法1和方法2中任选一种 ， 添加辅助线并完成证明.
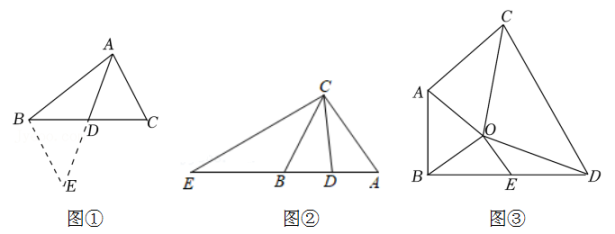
(2)、问题解决：如图2，在（1）的条件下，连接 ，当 时，探究线段 ， ， 之间的数量关系，并说明理由；(3)、问题拓展：如图3，在四边形 中， ， ，过点D作 ，垂足为点E，请直接写出线段 、 、 之间的数量关系.24. 【发现问题】小强在一次学习过程中遇到了下面的问题：如图①，AD是△ABC的中线，若AB＝5，AC＝3，求AD的取值范围．【探究方法】小强所在的小组通过探究发现，延长AD至点E，使ED＝AD．连接BE，可以证出△ADC≌△EDB，利用全等三角形的性质可将已知的边长与AD转化到到△ABE中，进而求出AD的取值范围．
方法小结：从上面的思路可以看出，解决问题的关键是将中线AD延长一倍，构造出全等三角形，我们把这种方法叫做“倍长中线法”．
(1)、请你利用上面解答问题的思路方法，写出求AD的取值范围的过程；(2)、【问题解决】如图②，CB是△AEC的中线，CD是△ABC的中线，且AB＝AC，下列四个选项中：
A．∠ACD＝∠BCD B．CE＝2CD C．∠BCD＝∠BCE D．CD＝CB
直接写出所有正确选项的序号是 ．
(3)、【问题拓展】如图③，在△ABO和△CDO中，OA＝OB，OC＝OD，∠AOB与∠COD互补，连接AC、BD，E是BD的中点，求证：OE＝AC．
-