2023-2024学年高中数学人教A版必修一 2.2 基本不等式

试卷更新日期：2023-08-06 类型：同步测试

进入出卷网下载

一、选择题

1. 若 $a > 0$ ， $b > 0$ ，且 $a + b = 6$ ，则 $a b$ 的最大值为（）

A、5 B、6 C、8 D、9

查看试题解析
2. 设实数 $x$ 满足 $x < 1$ ，则函数 $y = 2 x + 3 + \frac{1}{x - 1}$ 的最大值是（）

A、 $1 - 2 \sqrt{2}$ B、 $5 + 2 \sqrt{2}$ C、 $1 + 2 \sqrt{2}$ D、 $5 - 2 \sqrt{2}$

查看试题解析
3. 若 $a > 1 ， b > 1$ ，且a≠b，则 $a^{2} + b^{2} ， 2 a b ， a + b ， 2 \sqrt{a b}$ 中的最大值是（）

A、 $a^{2} + b^{2}$ B、 $2 a b$ C、 $a + b$ D、 $2 \sqrt{a b}$

查看试题解析
4. 已知x>0，y>0，且x＋2y＝4，则(1＋x)(1＋2y)的最大值为（）

A、36 B、4 C、16 D、9

查看试题解析
5. 已知 $x > y > 0$ ，且 $x^{2} - y^{2} = 1$ ，则 $2 x^{2} + 3 y^{2} - 4 x y$ 的最小值为（）

A、 $\frac{3}{4}$ B、1 C、 $\frac{17}{16}$ D、 $\frac{9}{8}$

查看试题解析
6. 若 $x > 0$ ， $y > 0$ ， $x + 3 y = 1$ ，则 $\frac{x y}{3 x + y}$ 的最大值为（）

A、 $\frac{1}{9}$ B、 $\frac{1}{12}$ C、 $\frac{1}{16}$ D、 $\frac{1}{20}$

查看试题解析
7. 已知 $x > 0$ ， $y > 0$ ，且满足 $x + 2 y - x y = 0$ ，则 $\frac{9}{2 x + y}$ 的最大值为（）

A、9 B、6 C、4 D、1

查看试题解析
8. 已知 $x ， y \in R$ ， $x^{2} + y^{2} + x y = 1$ ，则（）

A、 $x^{2} + y^{2}$ 的最大值为 $\frac{2}{3}$ 且 $x + y$ 的最大值为 $\frac{2 \sqrt{3}}{3}$ B、 $x^{2} + y^{2}$ 的最大值为 $\frac{2}{3}$ 且 $x + y$ 的最小值为0 C、 $x^{2} + y^{2}$ 的最小值为 $\frac{2}{3}$ 且 $x + y$ 的最大值为 $\frac{2 \sqrt{3}}{3}$ D、 $x^{2} + y^{2}$ 的最小值为 $\frac{2}{3}$ 且 $x + y$ 的最小值为0

查看试题解析
9. 已知 $x > 0$ ， $y > 0$ ，且 $\frac{2}{x} + \frac{1}{y} = 1$ ，则 $2 x + y + \frac{2 y}{x}$ 的最小值为（）

A、 $5 + 4 \sqrt{2}$ B、 $3 + 4 \sqrt{2}$ C、9 D、7

查看试题解析
10. 已知 $a ， b$ 为正实数，以下不等式成立的有（）
① $\frac{b}{a} > \frac{b + 1}{a + 1}$ ；② $a b + \frac{2}{a b} > 2$ ；③ $a^{2} + b^{2} > 4 a b - 4 b^{2}$ ；④ $| a - 1 | + | a | \geq 1$

A、②④ B、②③ C、②③④ D、①④

查看试题解析

二、多项选择题

11. 下列结论中正确的有（）

A、若命题“ $\exists x \in R$ ， $x^{2} + 4 x + m = 0$ ”为假命题，则实数 $m$ 的取值范围是 $(4 ， + \infty)$ B、若 $a ， b ， c \in R$ ，则“ $a b^{2} > c b^{2}$ ”的充要条件是“ $a > c$ ” C、“ $a > 1$ ”是“ $\frac{1}{a} < 1$ ”的充分不必要条件 D、当 $x > 0$ 时， $x + \frac{2}{x}$ 的最小值为 $2 \sqrt{2}$

查看试题解析
12. 已知 $a$ ， b为实数，且 $a b \neq 0$ ，则下列命题正确的是（）

A、若 $a > 0$ ， $b > 0$ ，则 $a + b \geq 2 \sqrt{a b}$ B、若 $a + b = 1$ ，则 $\frac{1}{a} + \frac{1}{b} \geq 4$ C、若 $a \neq b$ ，则 $a + b > 2 \sqrt{a b}$ D、若 $a + b > 2 \sqrt{a b}$ ，则 $a \neq b$

查看试题解析
13. 已知 $x > 0$ ， $y > 0$ ， $x^{2} + y^{2} = 1$ ，当且仅当 $x = y = \frac{\sqrt{2}}{2}$ 时，则下列结论正确的是（）

A、 $x y$ 取得最大值为 $\frac{1}{2}$ B、 $x y$ 取得最小值为 $\frac{1}{2}$ C、 $x + y$ 取得最大值为 $\sqrt{2}$ D、 $x + y$ 取得最小值为 $\sqrt{2}$

查看试题解析
14. 已知a， $b \in R$ ，且 $a b > 0$ ，则下列不等式成立的是（）

A、 $\frac{a + b}{2} \geq \sqrt{a b}$ B、 $a b \leq \frac{a^{2} + b^{2}}{2}$ C、 $\frac{b}{a} + \frac{a}{b} \geq 2$ D、 $\frac{2 a b}{a + b} \leq \frac{a + b}{2}$

查看试题解析
15. $a ， b > 0$ 且 $a + b = 1$ ，则 $\frac{4}{a} + \frac{1}{b}$ 的可能取值为（）

A、8 B、9 C、10 D、11

查看试题解析
16. 已知正实数x，y满足 $2 x + y = x y$ ，则（）

A、 $x y \geq 8$ B、 $x + y \geq 6$ C、 $\frac{1}{x - 1} + \frac{8}{y} \geq 4$ D、 $2 x^{2} y + y^{2} \geq 48$

查看试题解析

三、填空题

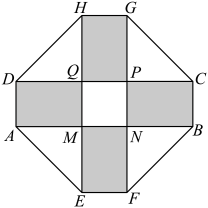
17. 若正实数 $x$ 、 $y$ 满足 $3 x + y = 1$ ，则 $\frac{12}{x} + \frac{1}{y}$ 的最小值为.

查看试题解析
18. 已知 $x > 0 ， y > 0$ ，且 $x + y = 1$ ，则 $\frac{3 x}{y} + \frac{1}{x y}$ 的最小值为.

查看试题解析
19. 已知 $x > - 2$ ，则 $x + \frac{9}{x + 2}$ 的最小值为．

查看试题解析
20. 某公园设计了一座八边形的绿化花园，它的主体造型平面图（如图2）是由两个相同的矩形ABCD和EFGH构成的面积为 $80 m^{2}$ 的十字型区域，计划在正方形MNPQ上建一座花坛，造价为99元/ $m^{2}$ ；在四个空角（图中四个三角形）上铺草坪，造价为8元/ $m^{2}$ ；在四个矩形（图中阴影部分）上不做任何设计．设总造价为S（单位：元），AD长为x（单位：m），则绿化花园总造价S的最小值为元．

查看试题解析
21. 设实数 $x$ 满足 $x > - 1$ ，函数 $y = 2 + 3 x + \frac{4}{x + 1}$ 的最小值为.

查看试题解析
22. 已知 $x > 0$ ， $y > 0$ ，满足 $x^{2} + 2 x y - 2 = 0$ ，则 $2 x + y$ 的最小值是．

查看试题解析

四、解答题

23.

(1)、在面积为定值 $S$ 的矩形中，边长是多少时矩形的周长最小？

(2)、在周长为定值 $P$ 的矩形中，边长是多少时矩形的面积最大？

查看试题解析
24. 已知 $m + 2 n = 2$ ．

(1)、当 $m > 0$ ， $n > 0$ 时，求 $\frac{1}{m} + \frac{2}{n}$ 的最小值；

(2)、当 $m > - 1$ ， $n > 0$ 时，求 $\frac{1}{m + 1} + \frac{2}{n}$ 的最小值．

查看试题解析
25. 已知 $a > 0$ ， $b > 0$ .

(1)、若 $b = 6 - \frac{1}{a}$ ，求 $\frac{b}{a}$ 的最大值；

(2)、若 $a^{2} + 9 b^{2} + 2 a b = a^{2} b^{2}$ ，证明： $a b \geq 8$ .

查看试题解析
26. 已知正实数 $a$ ， $b$ 满足 $\frac{1}{a} + \frac{1}{b} = 1$ .求

(1)、 $a + 2 b$ 的最小值；

(2)、 $\frac{4 a}{a - 1} + \frac{9 b}{b - 1}$ 的最小值；

(3)、 $16 a^{2} + b^{2} - 32 a - 2 b$ 的最小值.

查看试题解析
27. 已知 $m + 2 n = 2$ ，且 $m > - 1$ ， $n > 0$ .

(1)、求 $\frac{1}{m + 1} + \frac{2}{n}$ 的最小值；

(2)、求 $\frac{m^{2}}{2 n + 2} + \frac{4 n^{2}}{m + 1}$ 的最小值.

查看试题解析
28. 已知关于x的方程 $(1 + 2 k^{2}) x^{2} - 4 k m x + 2 m^{2} - 2 = 0$ 有两个不相等的实数根 $x_{1} ， x_{2}$ ．

(1)、证明： $m^{2} < 1 + 2 k^{2}$ ；

(2)、证明： $x_{1} x_{2} < 2$ ；

(3)、设 $S = | m | \cdot \sqrt{(x_{1} + x_{2})^{2} - 4 x_{1} x_{2}}$ ，求S的最大值．

查看试题解析