2023年浙教版数学八年级上册2.8 直角三角形全等的判定 同步测试（培优版）
试卷更新日期：2023-08-06 类型：同步测试
一、选择题（每题3分，共30分）
-
1. 如图，已知 于点 ， 于点 ，且 ， ， ，则 的度数为（ ）
A、 B、 C、 D、2. 如图，点P到 、 、 的距离恰好相等，则点P的位置：①在 的平分线上；②在 的平分线上；③在 的平分线上；④恰好是 、 、 三条平分线的交点．上述结论中，正确的个数有（ ）
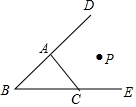A、 个 B、 个 C、 个 D、 个3. 如图，在四边形中， ， 平分 ， ， ， ， 分别是 ， 上的动点，当取得最小值时，的长是（ ）
A、8 B、10 C、12 D、164. 如图，在等腰△ 中， ， ，O是△ 外一点，O到三边的垂线段分别为 ， ， ，且 ，则 的长度为（ ）
A、5 B、6 C、 D、5. 如图，∠ABC＝40°，BD平分∠ABC，过D作DE∥AB交BC于点E，若点F在AB上，且满足DF＝DE，则∠DFB的度数为（ ）
A、20° B、140° C、40°或140° D、20°或140°6. 如图， 的外角 ， 的平分线 ， 相交于点P， 于E， 于F，下列结论：（1） ；（2）点P在 的平分线上；（3） ；（4）若 ，则 ，其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个7. 如图， 中， 的平分线 与边 的垂直平分线 相交于 交 的延长线于 于F，现有下列结论：① ；② ；③ 平分 ；④若 ，则 .其中正确的个数为（ ）
A、1个 B、2个 C、3个 D、4个8. 如图 是 的角平分线， 于E，点F，G分别是 ， 上的点，且 ， 与 的面积分别是10和3，则 的面积是（ ）
A、4 B、5 C、6 D、79. 如图，点P为定角∠AOB平分线上的一个定点，且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：①PM=PN；②OM+ON的值不变；③MN的长不变；④四边形PMON的面积不变，其中，正确结论的是（ ）
A、①②③ B、①②④ C、①③④ D、②③④10. 如图所示， 是 的角平分线， ，垂足为 ， ， 和 的面积分别为49，40，则 的面积为（ ）
A、3.5 B、4.5 C、9 D、10二、填空题（每空4分，共24分）
-
11. 如图所示，在等腰△ABC中，AB＝AC，∠B＝50°，D为BC的中点，点E在AB上，∠AED＝73°，若点P是等腰△ABC的腰上的一点，则当△EDP为以DE为腰的等腰三角形时，∠EDP的度数是.
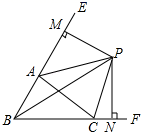
12. 如图，AP，BP分别平分△ABC内角∠CAB和外角∠CBD，连接CP，若∠ACP＝130°，则∠APB＝ ．
13. 如图， ABC中，∠ABC、∠EAC的角平分线BP、AP交于点P，延长BA、BC，PM⊥BE，PN⊥BF，则下列结论中正确的是.①CP平分∠ACF；②∠ABC＋2∠APC＝180°；③∠ACB＝2∠APB；④S△PAC＝S△MAP＋S△NCP.
14. 如图，已知等边和等边 ， 点P在BC的延长线上，EC的延长线交AP于点M，连接BM；下列结论：①；②；③BM平分；④ ， 其中正确的有（填序号）．
15. 如图，任意画一个∠BAC=60°的△ABC，再分别作△ABC的两条角平分线BE和CD，BE和CD相交于点P，连接AP，有以下结论：①∠BPC=120°；②AP平分∠BAC；③AD=AE；④PD=PE；⑤BD+CE=BC；其中正确的结论为 ． （填写序号）
16. 如图，在 ABC中，AH是高，AE BC，AB＝AE，在AB边上取点D，连接DE，DE＝AC，若 ，BH＝1，则BC＝.
三、综合题（共8题，共66分）
-
17. 定义：如果三角形的两个内角和满足 ， 那么我们称这样的三角形为“类直角三角形”.如图，在中， ， ， .请把这个三角形分割成两个三角形，使得其中一个为“类直角三角形”，并求出这个“类直角三角形”的面积.（备注：要求尺规作图）
18. 如图，在 中， 是角平分线， 于点 ， 在边AC上， .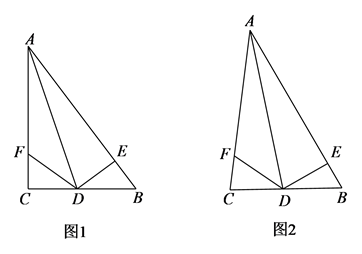
(1)、如图1，若 ，求证： ；(2)、如图2，求证： ；(3)、若 ， ， ，直接写出 的长.19. 已知在△ABC中，∠CAB的平分线AD与BC的垂直平分线DE交于点D，DM⊥AB于M，DN⊥AC的延长线于N.
(1)、证明：BM＝CN.(2)、当∠BAC＝70°时，求∠DCB的度数；(3)、若AB＝8，AC＝4，DE＝3，则4DN2﹣BC2的值为 .20. 如图，∠MAN是一个钝角，AB平分∠MAN，点C在射线AN上，且AB＝BC，BD⊥AC，垂足为D．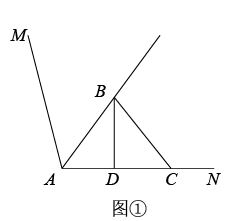
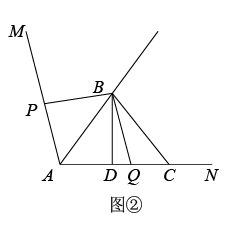
(1)、求证：；(2)、动点P，Q同时从A点出发，其中点Q以每秒3个单位长度的速度沿射线AN方向匀速运动；动点P以每秒1个单位长度的速度匀速运动．已知AC＝5，设动点P，Q的运动时间为t秒．①如图②，当点P在射线AM上运动时，若点Q在线段AC上，且 ， 求此时t的值；
②如图③，当点P在直线AM上运动时，点Q在射线AN上运动的过程中，是否存在某个时刻，使得APB与BQC全等？若存在，请求出t的值；若不存在，请说出理由．
21. △ABC中，∠ACB＝90°，AC＝BC ， 点D是射线BC上一点，连接AD ， 过点B作BF⊥AD于点F ， 直线BF、AC交于点E ．
(1)、如图1，当点D在线段BC的延长线上时，求证：AC＋CE＝BD；(2)、如图2，当点D在线段BC上时，求证：FC平分∠AFE；(3)、如图3，在（2）的条件下，若点D是BC的中点，△AFE的面积为36，求AF的长．22. 如图①，C、F分别为线段AD上的两个动点，BC⊥AD，垂足为C，EF⊥AD，垂足为F，且AB==DE，AF=CD，点G是AD与BE 的交点.
(1)、求证∶ BG=EG；(2)、当C、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立?若成立，请给予证明；若不成立，请说明理由.23. 如图，∠MON=90°，点A、B分别在射线OM、ON上，点C在∠MON内部．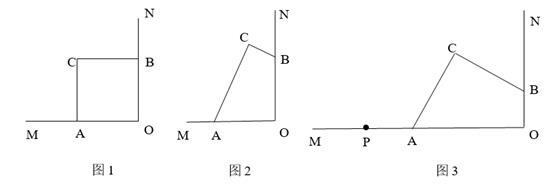
(1)、若OA=OB，①如图1，若CA⊥OM，CB⊥ON．求证：CA=CB．
②如图2，若∠ACB=90°．求证：OC平分∠ACB．
(2)、如图3，点A、B 分别在射线OM、ON上运动，点C随之运动，且∠ACB=90°，AC=BC．P为OM上一定点，当点C运动到何处时，PC的长度最短？请用尺规作图作出PC最短时C点的位置（保留作图痕迹，不要写作法），并请简要说明理由．
24. 在 中， .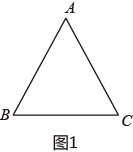
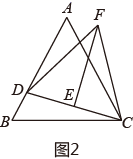
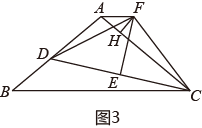(1)、如图1、求证： ：(2)、如图2，D为AB上一点，连接CD，E为CD中点，过点E作 于点E，连接 ，求证： ；(3)、如图3，在（2）的条件下，过点F作 于点H，连接AF，若 AF∥BC，FH=4，CH=20，BD=10 ，求 的面积