福建省福州市闽江口协作体2022-2023学年高二下学期期末考试数学试题
试卷更新日期:2023-08-04 类型:期末考试
一、单选题
-
1. 已知 , , 则( )A、 B、 C、 D、2. 已知 , 则“”是“”的( )A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既非充分又非必要条件3. 甲乙两人通过考试的概率分别为和 , 两人同时参加考试,其中恰有一人通过的概率是( )A、 B、 C、 D、4. 已知 , , ,则( )A、 B、 C、 D、5. 设 是函数 的导函数, 的图象如图所示,则 的图象最有可能的是( )
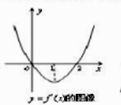 A、
A、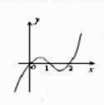 B、
B、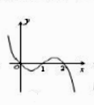 C、
C、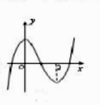 D、
D、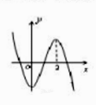 6. 已知平面的一个法向量为 , , 则直线与平面的位置关系为( )A、 B、 C、 D、相交但不垂直7. 函数 的零点所在的区间是( )A、 B、 C、 D、8. 若函数在上单调,则实数的取值范围是( )A、 B、 C、 D、
6. 已知平面的一个法向量为 , , 则直线与平面的位置关系为( )A、 B、 C、 D、相交但不垂直7. 函数 的零点所在的区间是( )A、 B、 C、 D、8. 若函数在上单调,则实数的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 已知复数 , 其共轭复数为 , 则( )A、的实部与虚部之和为 B、 C、是纯虚数 D、
三、单选题
-
10. 在下列四个正方体中,能得出的是( )A、
 B、
B、 C、
C、 D、
D、
四、多选题
-
11. 已知函数 , , , 的部分图像如图所示,则下列说法正确的是( )
 A、 B、的图像关于点对称 C、在上为增函数 D、把的图像向右平移个单位长度,得到一个奇函数的图象12. 已知是定义在上的不恒为零的函数,对于任意 , 都满足 , 则下述正确的是( )A、 B、 C、是偶函数 D、若 , 则
A、 B、的图像关于点对称 C、在上为增函数 D、把的图像向右平移个单位长度,得到一个奇函数的图象12. 已知是定义在上的不恒为零的函数,对于任意 , 都满足 , 则下述正确的是( )A、 B、 C、是偶函数 D、若 , 则五、填空题
-
13. 在平行六面体中,为与的交点,若存在实数 , 使向量 , 则 .14. 已知为单位向量,且 , 若 , 向量的夹角为 , 则 .15. 需要测量某塔的高度,选取与塔底在同一个水平面内的两个测量基点与 , 现测得 , , 米,在点处测得塔顶的仰角为 , 则塔高为米
 16. 已知 , 若 , 则实数的值可以为
16. 已知 , 若 , 则实数的值可以为六、解答题
-
17. 已知.(1)、当k为何值时,与共线?(2)、若= , = 且A,B,C三点共线,求m的值.18. 在① , ② , ③三个条件中任选一个,补充在下面问题中,并解答.
问题:已知 , , 分别为三个内角 , , 的对边,且____.
注:如果选择多个条件分别解答,按第一个解答计分.
(1)、求;(2)、若 , 则的面积为 , 求 , .19. 如图,已知四棱锥的底面是正方形,侧棱底面 , , 是的中点. (1)、证明:平面;(2)、求二面角的余弦值.20. 为庆祝建党周年,讴歌中华民族实现伟大复兴的奋斗历程,增进全体党员干部职工对党史的了解某单位组织开展党史知识竞赛活动,以支部为单位参加比赛现把名党员的成绩绘制了频率分布直方图,根据图中数据回答下列问题:
(1)、证明:平面;(2)、求二面角的余弦值.20. 为庆祝建党周年,讴歌中华民族实现伟大复兴的奋斗历程,增进全体党员干部职工对党史的了解某单位组织开展党史知识竞赛活动,以支部为单位参加比赛现把名党员的成绩绘制了频率分布直方图,根据图中数据回答下列问题: (1)、求的值及这名党员成绩的众数;(2)、若要选取成绩前的党员参加上一级的比赛,则应选取多少分以上的参赛?
(1)、求的值及这名党员成绩的众数;(2)、若要选取成绩前的党员参加上一级的比赛,则应选取多少分以上的参赛?
-
-