2023年浙教版数学八年级上册2.8直角三角形全等的判定 同步测试（提高版）
试卷更新日期：2023-08-04 类型：同步测试
一、选择题（每题3分，共30分）
-
1. 与三边长分别为3，4，5的三角形全等，满足条件的的边角可以是（ ）A、 ， ， B、 ， ， C、 ， ， D、 ， ，2. 已知：如图，∠GBC，∠BAC的平分线相交于点F，BE⊥CF于H，若∠AFB=40°，∠BCF的度数为（ ）
A、40° B、50° C、55° D、60°3. 如图，在四边形 中， ， ，点P是 边上的一动点，连接 ，若 ，则DP的长不可能是（ ）
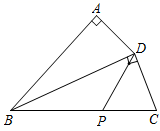A、2 B、3 C、4 D、54. 在 中， ，两个完全一样的三角尺按如图所示摆放.它们一组较短的直角边分别在 ， 上，另一组较长的对应边的顶点重合于点P， 交边 于点D，则下列结论错误的是（ ）
A、 平分 B、 C、 垂直平分 D、5. 小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是（ ）
A、角的内部到角的两边的距离相等的点在角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均错误6. 如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，BE平分∠ABC，CD⊥AB于D，BE与CD相交于F，则CF的长是（ ）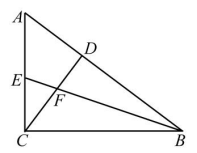
A、1 B、2 C、 D、7. 如图，△ABD和△CBD，∠ADB=90°，∠ABD=∠DBC，AD=DC=1，若AB=4，则BC的长为（ ）
A、 B、2 C、3 D、8. 如图，在中于点 ， 为上一点连结交于点 ， 若 ， ， 则与的和为（ ）
A、 B、 C、 D、9. 如图，在中， ， ， 垂足为 ， 平分 ， 交于点 ， 交于点若 ， ， 则的长为（ ）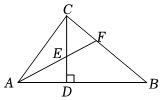
A、4 B、 C、 D、510. 如图，用三角尺可按下面方法画角平分线：在已知的∠AOB 的两边上分别取点M、N，使OM＝ON，再分别过点M、N作OA、OB的垂线，交点为P，画射线OP．可证得△POM≌△PON，OP平分∠AOB．以上依画法证明△POM≌△PON根据的是（ ）
A、SSS B、SAS C、AAS D、HL二、填空题（每空3分，共18分）
-
11. 如图，点O是 的两外角平分线的交点，下列结论：①；②点O到AB、AC的距离相等；③点O到的三边的距离相等；④点O在的平分线上.其中结论正确的是（填序号）.
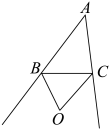12. 如图，点O在ABC内且到三边的距离相等．若∠A＝58°，则∠BOC＝度．
13. 如图，在Rt△ABC中，AC＝4，AB＝5，∠C＝90°，BD平分∠ABC交AC于点D，则BD的长是.
14. 如图，已知AD，CE是△ABC的两条高线，AD＝CE，∠CAD＝25°，则∠OCD＝度.
15. 在△???中，已知??：??：??=5：12：13，AD是△???的角平分线，??⊥??于点E.若△???的面积为9，则△???的面积为.16. 如图，已知和都是等边三角形，点 在同一条直线上，交于M，交于N， 交点O；下列说法：①；②为等边三角形；③；④平分∠.其中一定正确的是（只需填写序号）.
三、解答题（共9题，共72分）
-
17. 如图中， ， ， D是边上一点，连接 ， 垂足为点C，且 ， 交线段于点F．
(1)、在图1中画出正确的图形，并证明；(2)、当时，求证：平分 ．18. 如图，已知AD是△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，BE＝CF.
(1)、求证：△ABC是等腰三角形；(2)、若AB＝5，BC＝6，求DE的长.19. 数学课上，同学们兴致勃勃地探讨着利用不同画图工具画角的平分线的方法．小惠说：如图，我用两把完全相同的直尺可以作出角的平分线．画法如下：
①第一把直尺按图1所示放置，使一条边和射线对齐；
②第二把直尺按图2所示放置，使一条边和射线对齐；
如图3，两把直尺的另一条边相交于点P，作射线 ． 射线是的平分线．
小旭说：我用两个直角三角板可以画角的平分线．
小宇说：只用一把刻度尺就可以画角的平分线．
……
请你也参与探讨，解决以下问题：
(1)、小惠的做法符合题意吗？如果正确，请说明依据，如果错误，请说明理由；(2)、请你参考小旭或小宇的思路，或根据自己的思路，画出下图中的平分线，并简述画图的过程．
20. 如图，已知DE⊥AB垂足为E，DF⊥AC垂足为F，BD＝CD，BE＝CF.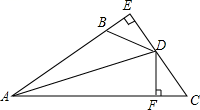
(1)、求证：AD平分∠BAC；(2)、丁丁同学观察图形后得出结论：AB+AC＝2AE，请你帮他写出证明过程.21. 如图，在中， ， 平分交于点 ， 作于点 ．
(1)、若 ， 求的度数．(2)、若 ， ．①求的长度；
②求的面积．
22. 如图，在中，、分别是边、上的高线.
(1)、如果 ， 那么是等腰三角形，请说明理由；(2)、取F为中点，连接点D ， E ， F得到 ， G是中点，求证：；(3)、在（2）的条件下，如果 ， 求的长度.23. 已知：点O到△ABC的两边AB、AC所在直线的距离OE、OF相等，且OB＝OC．(1)、如图，若点O在边BC上，求证：AB＝AC；
(2)、如图，若点O在△ABC的内部，则（1）中的结论还成立吗？若成立，请证明；若不成立，说明理由；
(3)、若点O在△ABC的外部，则（1）的结论还成立吗？请画图表示．24. 如图1，中，作的角平分线相交于点O，过点O作分别交于E、F.
(1)、①求证：；②若的周长是25， ， 试求出的周长.
(2)、如图2，若的平分线与外角的平分线相交于点P，连接 ， 试探求与的数量关系式.25. 综合与实践：问题情境：已知是的平分线，P是射线上的一点，点C，D分别在射线 ， 上，连接 ．
(1)、初步探究：如图1，当 ， 时，与的数量关系是；(2)、深入探究：如图2，点C，D分别在射线 ， 上运动，且 ， 当时，与在（1）中的数量关系还成立吗？请说明理由；(3)、拓展应用：如图3，如果点C在射线上运动，且 ， 当时，点D落在了射线的反向延长线上，若点P到的距离为3， ， 求的长（直接写出答案）．