2023年浙教版数学八年级上册2.8 直角三角形全等的判定 同步测试(基础版)
试卷更新日期:2023-08-04 类型:同步测试
一、选择题(每题3分,共30分)
-
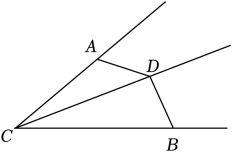
1. 如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充的条件是( )
 A、AC=AD或BC=BD B、AC=AD且BC=BD C、∠BAC=∠BAD D、以上都不对2. 如图,已知 , 添加下列条件后不能使的是( )
A、AC=AD或BC=BD B、AC=AD且BC=BD C、∠BAC=∠BAD D、以上都不对2. 如图,已知 , 添加下列条件后不能使的是( ) A、 B、 C、 D、3. 如图,在中, , 是高,能直接判断的依据是( )
A、 B、 C、 D、3. 如图,在中, , 是高,能直接判断的依据是( ) A、 B、 C、 D、4. 如图,在和中, , , , 则( )
A、 B、 C、 D、4. 如图,在和中, , , , 则( )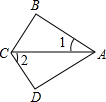 A、30° B、40° C、50° D、60°5. 如下图,要用“HL”判断Rt△ABC和Rt△DEF全等的条件是( )
A、30° B、40° C、50° D、60°5. 如下图,要用“HL”判断Rt△ABC和Rt△DEF全等的条件是( ) A、AC=DF,BC=EF B、∠A=∠D,AB=DE C、AC=DF,AB=DE D、∠B=∠E,BC=EF6. 如图, , ,垂足分别是E,F,且 ,若利用“ ”证明 ,则需添加的条件是( )
A、AC=DF,BC=EF B、∠A=∠D,AB=DE C、AC=DF,AB=DE D、∠B=∠E,BC=EF6. 如图, , ,垂足分别是E,F,且 ,若利用“ ”证明 ,则需添加的条件是( ) A、 B、 C、 D、7. 如图,DE⊥AC于点E,BF⊥AC于点F,且DE=BF,若利用“HL”证明△DEC≌△BFA,则需添加的条件是( )
A、 B、 C、 D、7. 如图,DE⊥AC于点E,BF⊥AC于点F,且DE=BF,若利用“HL”证明△DEC≌△BFA,则需添加的条件是( ) A、DC=BA B、EC=FA C、∠D=∠B D、∠DCE=BAF8. 下列判定直角三角形全等的方法,不正确的是( )A、两条直角边对应相等。 B、斜边和一锐角对应相等。 C、斜边和一条直角边对应相等。 D、两锐角相等。9. 如图,△ABC的两个外角的平分线相交于点P,则下列结论正确的是( )
A、DC=BA B、EC=FA C、∠D=∠B D、∠DCE=BAF8. 下列判定直角三角形全等的方法,不正确的是( )A、两条直角边对应相等。 B、斜边和一锐角对应相等。 C、斜边和一条直角边对应相等。 D、两锐角相等。9. 如图,△ABC的两个外角的平分线相交于点P,则下列结论正确的是( )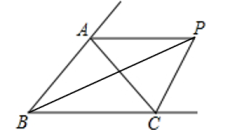 A、BP平分∠APC B、BP平分∠ABC C、BA=BC D、PA=PC10. 如图,在Rt△ABC中,∠C=90˚,AD平分∠BAC , 交BC于点D , AB=10,S△ABD=25,则CD的长为( )
A、BP平分∠APC B、BP平分∠ABC C、BA=BC D、PA=PC10. 如图,在Rt△ABC中,∠C=90˚,AD平分∠BAC , 交BC于点D , AB=10,S△ABD=25,则CD的长为( ) A、2.5 B、4 C、5 D、10
A、2.5 B、4 C、5 D、10二、填空题(每空3分,共30分)
-
11. 如图,某小区广场有两个长度相等的滑梯靠在一面墙上,已知左边滑梯水平方向的长度AB与右边滑梯的高度DE相等.若右边滑梯与地面的夹角∠DFE=55°,则∠ABC的度数为°.
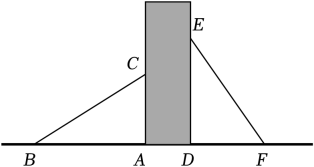 12. 如图,为中斜边上的一点,且 , 过点作的垂线,交于点 , 若 , , 则.
12. 如图,为中斜边上的一点,且 , 过点作的垂线,交于点 , 若 , , 则. 13. 如图,BE,CD是△ABC的高,且BD=EC,判定△BCD≌△CBE的依据是“”.
13. 如图,BE,CD是△ABC的高,且BD=EC,判定△BCD≌△CBE的依据是“”. 14. 如图所示,在中,于点 , 且 , 则度.
14. 如图所示,在中,于点 , 且 , 则度. 15. 在△ABC中,AD⊥BC于D,要用“HL”证明Rt△ADB≌Rt△ADC,则需添加的条件是.16. 如图, 中, 于D,要使 ,若根据“ ”判定,还需要加条件
15. 在△ABC中,AD⊥BC于D,要用“HL”证明Rt△ADB≌Rt△ADC,则需添加的条件是.16. 如图, 中, 于D,要使 ,若根据“ ”判定,还需要加条件 17. 有和一条对应相等的两个直角三角形全等,简写成“斜边直角边”或用字母表示为“”.18. 如图,若于B,于C,且 , , , 则.
17. 有和一条对应相等的两个直角三角形全等,简写成“斜边直角边”或用字母表示为“”.18. 如图,若于B,于C,且 , , , 则.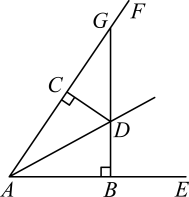
三、解答题(共7题,共60分)
-
19. 如图,已知AD是△ABC的边BC上的高,E为AD上一点,且BE=AC,DE=DC.
求证:∠DBE=∠DAC.
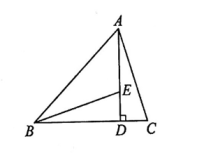 20. 如图,在中,是的中点, , , 垂足分别是点、 , . 求证:平分 .
20. 如图,在中,是的中点, , , 垂足分别是点、 , . 求证:平分 . 21. 已知,如图AC平分∠BAD,CE⊥AB于E点,CF⊥AD于F点,且BC=DC.求证:BE=DF.
21. 已知,如图AC平分∠BAD,CE⊥AB于E点,CF⊥AD于F点,且BC=DC.求证:BE=DF. 22. 如图,AD=BD,∠CAD+∠CBD=180°,求证:CD平分∠ACB.
22. 如图,AD=BD,∠CAD+∠CBD=180°,求证:CD平分∠ACB.