2023年浙教版数学八年级上册2.7 探索勾股定理 同步测试(培优版)
试卷更新日期:2023-08-04 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,长方体的高为9dm,底面是边长为6dm的正方形,如果一只蚂蚁从顶点A开始爬向顶点B,那么它爬行的最短路程为( )
 A、10dm B、12dm C、13dm D、15dm2. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.过点D作DF的垂线交小正方形对角线EF的延长线于点G,连结BG,若大正方形的面积是小正方形面积的5倍,则 的值为( )
A、10dm B、12dm C、13dm D、15dm2. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.过点D作DF的垂线交小正方形对角线EF的延长线于点G,连结BG,若大正方形的面积是小正方形面积的5倍,则 的值为( ) A、 B、3 C、 D、43. 如图,在等腰直角三角形中, , 为的中点,为边上一点不与端点重合 , 过点作于点 , 作于点 , 过点作交的延长线于点若 , 则阴影部分的面积为( )
A、 B、3 C、 D、43. 如图,在等腰直角三角形中, , 为的中点,为边上一点不与端点重合 , 过点作于点 , 作于点 , 过点作交的延长线于点若 , 则阴影部分的面积为( ) A、12 B、12.5 C、13 D、13.54. 三国时期的赵爽利用图1证明了勾股定理,后来日本的数学家关孝和在“赵爽弦图”的启发下利用图2也证明了勾股定理.在图2中,E,B,F在同一条直线上,四边形ABCD,EFGA,HGDJ都是正方形,若正方形ABCD的面积等于100,△IJD面积等于 , 且已知AH=2,则△KCD的面积等于( )
A、12 B、12.5 C、13 D、13.54. 三国时期的赵爽利用图1证明了勾股定理,后来日本的数学家关孝和在“赵爽弦图”的启发下利用图2也证明了勾股定理.在图2中,E,B,F在同一条直线上,四边形ABCD,EFGA,HGDJ都是正方形,若正方形ABCD的面积等于100,△IJD面积等于 , 且已知AH=2,则△KCD的面积等于( ) A、 B、39 C、 D、525. 如图,O是正内一点, , , , , 将线段BO以点B为旋转中心逆时针旋转60°得到线段 , 下列结论:①点O与的距离为6;②;③;④;⑤点P为内一点,则点P到三个顶点的距离和最小为.其中正确的结论是( )
A、 B、39 C、 D、525. 如图,O是正内一点, , , , , 将线段BO以点B为旋转中心逆时针旋转60°得到线段 , 下列结论:①点O与的距离为6;②;③;④;⑤点P为内一点,则点P到三个顶点的距离和最小为.其中正确的结论是( ) A、①②③⑤ B、①③④ C、②③④⑤ D、①②⑤6. 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BNMC,四块阴影部分的面积分别S1、S2、S3、S4 . 则等于( )
A、①②③⑤ B、①③④ C、②③④⑤ D、①②⑤6. 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BNMC,四块阴影部分的面积分别S1、S2、S3、S4 . 则等于( ) A、4 B、6 C、8 D、127. 在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:
A、4 B、6 C、8 D、127. 在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:①AE+BF=AB;②△DEF始终为等腰直角三角形;③S四边形CEDF=AB2;④AE2+CE2=2DF2 .
其中正确的是( )
 A、①②③④ B、①②③ C、①④ D、②③8. 如图,在△ABC中,∠ACB=90°,以△ABC的各边为边分别作正方形BAHI,正方形BCFG与正方形CADE,延长BG,FG分别交AD,DE于点K,J,连结DH,IJ.图中两块阴影部分面积分别记为S1 , S2.若S1:S2=1:4,S四边形边BAHE=18,则四边形MBNJ的面积为( )
A、①②③④ B、①②③ C、①④ D、②③8. 如图,在△ABC中,∠ACB=90°,以△ABC的各边为边分别作正方形BAHI,正方形BCFG与正方形CADE,延长BG,FG分别交AD,DE于点K,J,连结DH,IJ.图中两块阴影部分面积分别记为S1 , S2.若S1:S2=1:4,S四边形边BAHE=18,则四边形MBNJ的面积为( ) A、5 B、6 C、8 D、99. 如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°, , 则下列结论:①∠CAD=30° ② ③S平行四边形ABCD=AB•AC ④ ,正确的个数是( )
A、5 B、6 C、8 D、99. 如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°, , 则下列结论:①∠CAD=30° ② ③S平行四边形ABCD=AB•AC ④ ,正确的个数是( )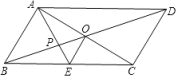 A、1 B、2 C、3 D、410. 如图,在平面直角坐标系xOy中,已知直线AB与y轴交于点A(0,6),与x轴的负半轴交于点B , 且∠BAO=30°, M、N是该直线上的两个动点,且MN=2,连接OM、ON , 则△MON周长的最小值为 ( )
A、1 B、2 C、3 D、410. 如图,在平面直角坐标系xOy中,已知直线AB与y轴交于点A(0,6),与x轴的负半轴交于点B , 且∠BAO=30°, M、N是该直线上的两个动点,且MN=2,连接OM、ON , 则△MON周长的最小值为 ( ) A、2+3 B、2+2 C、2+2 D、5+
A、2+3 B、2+2 C、2+2 D、5+二、填空题(每空3分,共24分)
-
11. 如图,圆柱底面半径为 , 高为 , 点A,B分别是圆柱两底面圆周上的点,且A,B在同一条竖直直线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为cm.
 12. 如图,在平面直角坐标系xOy中,直线与坐标轴交于A,B两点,于点C,P是线段OC上的一个动点,连接AP,将线段AP绕点A逆时针旋转 , 得到线段 , 连接 , 则线段的最小值为 .
12. 如图,在平面直角坐标系xOy中,直线与坐标轴交于A,B两点,于点C,P是线段OC上的一个动点,连接AP,将线段AP绕点A逆时针旋转 , 得到线段 , 连接 , 则线段的最小值为 .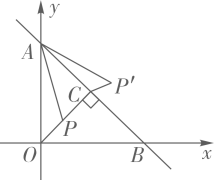 13. 气动升降桌由于高度可调节,给人们学习生活带来许多便捷.如图1所示是桌子的侧平面示意图,AC,BC,DC,DE,HG是固定钢架,HG垂直桌面MN,GE是位置可变的定长钢架.DF是两端固定的伸缩杆,其中,DE=20cm,GE=39cm,GF=13cm,∠EDC是一个固定角为150°,当GE旋转至水平位置时,伸缩杆最短,此时伸缩杆DF的长度为 cm.点D的离地高度为60cm,HG=10cm,小南将桌子调整到他觉得最舒服的高度,此时发现FD=FE,则桌面高度为 cm.
13. 气动升降桌由于高度可调节,给人们学习生活带来许多便捷.如图1所示是桌子的侧平面示意图,AC,BC,DC,DE,HG是固定钢架,HG垂直桌面MN,GE是位置可变的定长钢架.DF是两端固定的伸缩杆,其中,DE=20cm,GE=39cm,GF=13cm,∠EDC是一个固定角为150°,当GE旋转至水平位置时,伸缩杆最短,此时伸缩杆DF的长度为 cm.点D的离地高度为60cm,HG=10cm,小南将桌子调整到他觉得最舒服的高度,此时发现FD=FE,则桌面高度为 cm.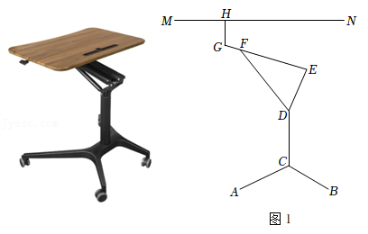 14. 如图,在中, , 于点 , 于点若 , .
14. 如图,在中, , 于点 , 于点若 , . (1)、的长为;(2)、在的腰上取一点 , 当是等腰三角形时,长为.15. 如图,在中, , 为边的中点,、分别为边、上的点,且 , 若 , , 则 , 线段的长度 .
(1)、的长为;(2)、在的腰上取一点 , 当是等腰三角形时,长为.15. 如图,在中, , 为边的中点,、分别为边、上的点,且 , 若 , , 则 , 线段的长度 . 16. 如图,一次函数y=-x+3的图象与x轴交于点A,与y轴交于点B,C是x轴上一动点,连接BC,将△ABC沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为.
16. 如图,一次函数y=-x+3的图象与x轴交于点A,与y轴交于点B,C是x轴上一动点,连接BC,将△ABC沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为. 17. 如图,在中. , 平分交于E,于D.下列结论:①;②点E在线段的垂直平分线上:③;④;⑤ , 其中正确的有(填结论正确的序号).
17. 如图,在中. , 平分交于E,于D.下列结论:①;②点E在线段的垂直平分线上:③;④;⑤ , 其中正确的有(填结论正确的序号).
三、综合题(共7题,共66分)
-
18. 已知 , , 为正数,满足如下两个条件:
①
②
证明:以 , , 为三边长可构成一个直角三角形.
19. 如图,直线经过原点O,点A在x轴上,于点D,于点F,已知点 , , , , 求的长度. 20. 在同一平面内的两个图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M,N间的“最距离”,记作: .
20. 在同一平面内的两个图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M,N间的“最距离”,记作: .如图,点B,C在数轴上表示的数分别为0,2,于点B,且 .
 (1)、若点D在数轴上表示的数为5,求d(点D,);(2)、若点E,F在数轴上表示的数分别是x, , 当d(线段 , )时,求x的取值范围.21. 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角处
(1)、若点D在数轴上表示的数为5,求d(点D,);(2)、若点E,F在数轴上表示的数分别是x, , 当d(线段 , )时,求x的取值范围.21. 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角处 (1)、请你在下面网格(每个小正方形边长为1)中,画出蚂蚁能够最快到达目的地的可能路径;(2)、当 , , 时,求蚂蚁爬过的最短路径的长;(3)、我们发现,“用不同的方式表示同一图形的面积”可以解决计算线段的有关问题,这种方法称为“面积法”.请“面积法”求点到最短路径的距离.22. 如图,在中, , 点为边上异于 , 的一个动点,作点关于的对称点 , 连结 , , 交直线于点.
(1)、请你在下面网格(每个小正方形边长为1)中,画出蚂蚁能够最快到达目的地的可能路径;(2)、当 , , 时,求蚂蚁爬过的最短路径的长;(3)、我们发现,“用不同的方式表示同一图形的面积”可以解决计算线段的有关问题,这种方法称为“面积法”.请“面积法”求点到最短路径的距离.22. 如图,在中, , 点为边上异于 , 的一个动点,作点关于的对称点 , 连结 , , 交直线于点. (1)、若 , , 是边上的高线.
(1)、若 , , 是边上的高线.①求线段的长;
②当时,求线段的长;
(2)、在的情况下,当是等腰三角形时,直接写出的度数.23. 如图,在边长为的正方形中,过中点E作正 , 过点F的直线分别交边、于点G、H、已知点M、N分别是线段、的动点,且是等边三角形.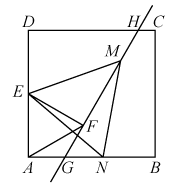 (1)、判断与的位置关系,并说明理由.(2)、当点N在线段上时
(1)、判断与的位置关系,并说明理由.(2)、当点N在线段上时①求证:
②试判断的结果是否变化?若变化,请说明理由;若不变,请求出这个值.
(3)、设 , 点A关于的对称点为 , 若点落在的内部,请直接写出的范围.24. 定义:若三角形满足:两边的平方和与这两边乘积的差等于第三边的平方,则称这个三角形为“类勾股三角形”.如图1在中, , 则是“类勾股三角形”. (1)、等边三角形一定是“类勾股三角形”,是命题(填真或假).(2)、若中, , 且 , 若是“类勾股三角形”,求的度数.(3)、如图2,在等边三角形的边上各取一点 , , 且相交于点 , 是的高,若是“类勾股三角形”,且.
(1)、等边三角形一定是“类勾股三角形”,是命题(填真或假).(2)、若中, , 且 , 若是“类勾股三角形”,求的度数.(3)、如图2,在等边三角形的边上各取一点 , , 且相交于点 , 是的高,若是“类勾股三角形”,且.①求证:.
②连结 , 若 , 那么线段能否构成一个“类勾股三角形”?若能,请证明;若不能,请说明理由.