2023年浙教版数学八年级上册2.7 探索勾股定理 同步测试(提高版)
试卷更新日期:2023-08-04 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 已知的三条边分别为a,b,c,下列条件不能判断是直角三角形的是( )A、 B、 , , C、 D、2. 如图,在边长为1的正方形方格中,A,B,C,D均为格点,构成图中三条线段 , , .现在取出这三条线段 , , 首尾相连拼三角形.下列判断正确的是( )
 A、能拼成一个锐角三角形 B、能拼成一个直角三角形 C、能拼成一个钝角三角形 D、不能拼成三角形3. 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是( )
A、能拼成一个锐角三角形 B、能拼成一个直角三角形 C、能拼成一个钝角三角形 D、不能拼成三角形3. 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是( ) A、10 B、 C、10或 D、10或4. 如图,在直线l上有正方形a,b,c,若a,c的面积分别为4和16,则b的面积为( )
A、10 B、 C、10或 D、10或4. 如图,在直线l上有正方形a,b,c,若a,c的面积分别为4和16,则b的面积为( ) A、24 B、20 C、12 D、225. 我国汉代的赵爽在注释《周髀算经》时给出了勾股定理的无字证明,人们称它为“赵爽弦图”,“赵爽弦图”指的是( )A、
A、24 B、20 C、12 D、225. 我国汉代的赵爽在注释《周髀算经》时给出了勾股定理的无字证明,人们称它为“赵爽弦图”,“赵爽弦图”指的是( )A、 B、
B、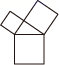 C、
C、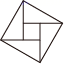 D、
D、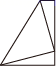 6. 1876年,美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边 , 在一条直线上,证明中用到的面积相等关系是( )
6. 1876年,美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边 , 在一条直线上,证明中用到的面积相等关系是( ) A、 B、 C、 D、7. 图中字母所代表的正方形的面积为175的选项为( )A、
A、 B、 C、 D、7. 图中字母所代表的正方形的面积为175的选项为( )A、 B、
B、 C、
C、 D、
D、 8. 如图,在“庆国庆,手拉手”活动中,某小组从营地A出发,沿北偏东方向走了1200m到达B点,然后再沿北偏西方向走了500m到达目的地C点,此时A,C两点之间的距离为( )
8. 如图,在“庆国庆,手拉手”活动中,某小组从营地A出发,沿北偏东方向走了1200m到达B点,然后再沿北偏西方向走了500m到达目的地C点,此时A,C两点之间的距离为( ) A、1000m B、1100m C、1200m D、1300m9. 勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.如图,秋千静止时,踏板离地的垂直高度 , 将它往前推至处时(即水平距离),踏板离地的垂直高度 , 它的绳索始终拉直,则绳索的长是( )
A、1000m B、1100m C、1200m D、1300m9. 勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.如图,秋千静止时,踏板离地的垂直高度 , 将它往前推至处时(即水平距离),踏板离地的垂直高度 , 它的绳索始终拉直,则绳索的长是( ) A、 B、 C、6 D、10. 《九章算术》中记录了这样一则“折竹抵地”问题:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)如果我们假设折断后的竹子高度为尺,根据题意,可列方程为( )
A、 B、 C、6 D、10. 《九章算术》中记录了这样一则“折竹抵地”问题:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)如果我们假设折断后的竹子高度为尺,根据题意,可列方程为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
11. 如图是“赵爽弦图”,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果AB=10,EF=2,那么AH等于
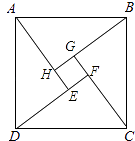 12. 如图所示的一块地,∠ADC=90°,CD=3,AD=4,AB=13,BC=12,求这块地的面积为.
12. 如图所示的一块地,∠ADC=90°,CD=3,AD=4,AB=13,BC=12,求这块地的面积为. 13. 如图,将一张长方形纸片按图中那样折叠,若 , , 则重叠部分(阴影)的面积是 .
13. 如图,将一张长方形纸片按图中那样折叠,若 , , 则重叠部分(阴影)的面积是 . 14. 如图,中, , , , 是的中点,是上一动点,则的最小值为.
14. 如图,中, , , , 是的中点,是上一动点,则的最小值为. 15. 如图,一架梯子AB长5米,底端离墙的距离BC为3米,当梯子下滑到DE时,米,则BE=米.
15. 如图,一架梯子AB长5米,底端离墙的距离BC为3米,当梯子下滑到DE时,米,则BE=米.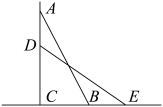 16. 如图是某路口处草坪的一角,当行走路线是时,有人为了抄近道而避开路的拐角 , 于是在草坪内走出了一条不该有的捷径路.某学习实践小组通过测量可知,的长约为6米,的长约为8米,为了提醒居民爱护草坪,他们想在A,处设立“踏破青白可惜,多行数步无妨”的提示牌.则提示牌上的“多行数步”是指多行米.
16. 如图是某路口处草坪的一角,当行走路线是时,有人为了抄近道而避开路的拐角 , 于是在草坪内走出了一条不该有的捷径路.某学习实践小组通过测量可知,的长约为6米,的长约为8米,为了提醒居民爱护草坪,他们想在A,处设立“踏破青白可惜,多行数步无妨”的提示牌.则提示牌上的“多行数步”是指多行米.
三、解答题(共10题,共72分)
-
17. 如图,一块四边形的空地, , AB的长为9m,BC的长为12m,CD的长为8m,AD的长为17m.为了绿化环境,计划在此空地上铺植草坪,若每铺植草坪需要花费30元,则此块空地全部铺植草坪共需花费多少元?
 18. 做4个全等的直角三角形,设它们的两条直角边分别为a , b , 斜边为c , 再做一个边长为c的正方形,把它们按如图的方式拼成正方形,请用这个图证明勾股定理.
18. 做4个全等的直角三角形,设它们的两条直角边分别为a , b , 斜边为c , 再做一个边长为c的正方形,把它们按如图的方式拼成正方形,请用这个图证明勾股定理. 19. 如图,有两棵树,一棵高6m,另一棵高2m,两树相距5m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?(结果精确到0.1m)
19. 如图,有两棵树,一棵高6m,另一棵高2m,两树相距5m.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?(结果精确到0.1m) 20. 如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处?
20. 如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处? 21. 我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法,请你用等面积法来探究下列两个问题:
21. 我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法,请你用等面积法来探究下列两个问题: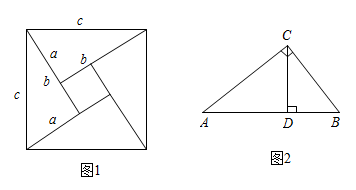 (1)、如图是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请用它验证勾股定理(2)、如图 , 在中, , 是边上的高, , , 求的长度(3)、如图①,若大正方形的面积是 , 小正方形的面积是 , 求的值.22. 八(1)班小明和小亮同学学习了“勾股定理”之后,为了测得下图风筝CE的高度,他们进行了如下操作:
(1)、如图是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请用它验证勾股定理(2)、如图 , 在中, , 是边上的高, , , 求的长度(3)、如图①,若大正方形的面积是 , 小正方形的面积是 , 求的值.22. 八(1)班小明和小亮同学学习了“勾股定理”之后,为了测得下图风筝CE的高度,他们进行了如下操作:①测得BD的长度为24米;
②根据手中剩余线的长度计算出风筝线BC的长为30米;
③牵线放风筝的小明身高AB为1.68米.
 (1)、求风筝的高度CE;(2)、若小亮让风筝沿CD方向下降了8米到点M(即CM=8米),则他往回收线多少米?23. 台风是一种自然灾害,它在以台风中心为圆心,一定长度为半径的圆形区域内形成极端气候,有极强的破坏力.如图,监测中心监测到一台风中心沿监测点B与监测点A所在的直线由东向西移动,已知点C为一海港,且点C与A,B两点的距离分别为300km、400km,且 , 过点作于点 , 以台风中心为圆心,半径为260km的圆形区域内为受影响区域,台风的速度为25km/h.
(1)、求风筝的高度CE;(2)、若小亮让风筝沿CD方向下降了8米到点M(即CM=8米),则他往回收线多少米?23. 台风是一种自然灾害,它在以台风中心为圆心,一定长度为半径的圆形区域内形成极端气候,有极强的破坏力.如图,监测中心监测到一台风中心沿监测点B与监测点A所在的直线由东向西移动,已知点C为一海港,且点C与A,B两点的距离分别为300km、400km,且 , 过点作于点 , 以台风中心为圆心,半径为260km的圆形区域内为受影响区域,台风的速度为25km/h. (1)、求监测点A与监测点B之间的距离;(2)、请判断海港C是否会受此次台风的影响,若受影响,则台风影响该海港多长时间?若不受影响,请说明理由.24. 定义:如图,点M,N把线段AB分割成AM,MN,NB,若以AM,MN,NB为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
(1)、求监测点A与监测点B之间的距离;(2)、请判断海港C是否会受此次台风的影响,若受影响,则台风影响该海港多长时间?若不受影响,请说明理由.24. 定义:如图,点M,N把线段AB分割成AM,MN,NB,若以AM,MN,NB为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点. (1)、已知M,N把线段AB分割成AM,MN,NB,若AM= 1,MN=2,BN= , 则点M,N是线段AB的勾股分割点吗?请说明理由.(2)、已知点M,N是线段AB的勾股分割点,且AM为直角边,若AB=12,AM=5,求BN的长.25. 如图,在中, , 点为边上异于 , 的一个动点,作点关于的对称点 , 连结 , , 交直线于点.
(1)、已知M,N把线段AB分割成AM,MN,NB,若AM= 1,MN=2,BN= , 则点M,N是线段AB的勾股分割点吗?请说明理由.(2)、已知点M,N是线段AB的勾股分割点,且AM为直角边,若AB=12,AM=5,求BN的长.25. 如图,在中, , 点为边上异于 , 的一个动点,作点关于的对称点 , 连结 , , 交直线于点. (1)、若 , , 是边上的高线.
(1)、若 , , 是边上的高线.①求线段的长;
②当时,求线段的长;
(2)、在的情况下,当是等腰三角形时,直接写出的度数.26. 综合与实践美丽的弦图中蕴含着四个全等的直角三角形.
 (1)、如图1,弦图中包含了一大一小两个正方形,已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c,结合图1,试验证勾股定理;(2)、如图2,将这四个直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(实线)的周长为24, , 求该飞镖状图案的面积;(3)、如图3,将八个全等的直角三角形紧密地拼接,记图中正方形 , 正方形 , 正方形的面积分别为 , 若 , 求的值.
(1)、如图1,弦图中包含了一大一小两个正方形,已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c,结合图1,试验证勾股定理;(2)、如图2,将这四个直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(实线)的周长为24, , 求该飞镖状图案的面积;(3)、如图3,将八个全等的直角三角形紧密地拼接,记图中正方形 , 正方形 , 正方形的面积分别为 , 若 , 求的值.