2023年浙教版数学八年级上册2.7 探索勾股定理 同步测试(基础版)
试卷更新日期:2023-08-04 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )A、2、3、4 B、4、5、6 C、5、11、12 D、8、15、172. 以下列各组数为边长,能构成直角三角形的是( )A、 , , 2 B、1,2, C、1, , D、4,5,63. 下列各组线段中,不能构成直角三角形的一组是( )A、 , 1, B、1, , 2 C、6,8,10 D、4,4,54. 一个直角三角形的两边长分别为4cm、3cm,则第三条边长为( )A、5cm B、4cm C、cm D、5cm 或cm5. 在等腰中, , , 则底边上的高为( )A、12 B、 C、 D、186. 直角三角形的一条直角边长是8cm,另一条直角边比斜边短2cm,则斜边长为( )A、12 cm B、15 cm C、17 cm D、20 cm7. 直角三角形两直角边长度为5,12,则斜边上的高( )A、6 B、8 C、13 D、8. 在中, , , , 则的长为( )A、5 B、10 C、 D、289. 如图,在△ABC中,AB=AC=10,BC=12,AD平分∠BAC,则AD等于( )
 A、6 B、7 C、8 D、910. 如图,在△ABC中,∠BAC=90°,AB=8,AC=6,点D为 BC 的中点,则AD 的长为( )
A、6 B、7 C、8 D、910. 如图,在△ABC中,∠BAC=90°,AB=8,AC=6,点D为 BC 的中点,则AD 的长为( ) A、4.8 B、5 C、6 D、8
A、4.8 B、5 C、6 D、8二、填空题(每空4分,共24分)
-
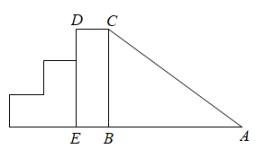
11. 已知一个三角形的三边长分别是4cm、7cm、6cm,该三角形的形状(填“是”或“不是”)直角三角形.12. 直角三角形两条边长分别为3和4,则第三边的长为.13. 三角形的三边长分别为3,4,5,则最长边上的高为 .14. 如图是一个滑梯示意图,左边是楼梯,右边是滑道,已知滑道与的长度相等,滑梯的高度 , .则滑道的长度为m.
 15. 如图,在Rt△ABC中,∠B=90°,分别以A,C为圆心,大于AC长为半径画弧,两弧相交于点M,N,作直线MN,与AC,BC分别交于点D,点E,连结AE,当AC=13,AB=5时,则△ABE的周长是.
15. 如图,在Rt△ABC中,∠B=90°,分别以A,C为圆心,大于AC长为半径画弧,两弧相交于点M,N,作直线MN,与AC,BC分别交于点D,点E,连结AE,当AC=13,AB=5时,则△ABE的周长是. 16. 已知 , , 那么以a、b为边长的直角三角形斜边上的中线长为 .
16. 已知 , , 那么以a、b为边长的直角三角形斜边上的中线长为 .三、解答题(共10题,共66分)
-
17. 已知:如图,四边形ABCD中,∠ACB=90°,AB=15,BC=9,AD=5,DC=13,
求证:△ACD是直角三角形.
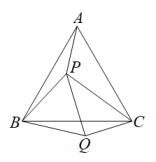
 18. 在中,D是BC上一点,AC=10,CD=6,AD=8,AB=17,求BC的长.
18. 在中,D是BC上一点,AC=10,CD=6,AD=8,AB=17,求BC的长. 19. 已知的三条边长分别为 , , , 其中 , , , 且是直角三角形吗?请证明你的判断.20. 如图,正方形网格中的每个小方格边长均为1,的顶点在格点上,判断的形状,并说明理由.
19. 已知的三条边长分别为 , , , 其中 , , , 且是直角三角形吗?请证明你的判断.20. 如图,正方形网格中的每个小方格边长均为1,的顶点在格点上,判断的形状,并说明理由. 21. 如图,某校攀岩墙的顶部A处安装了一根安全绳 , 让它垂到地面时比墙高多出了2米,教练把绳子的下端C拉开8米后,发现其下端刚好接触地面(即米), , 求攀岩墙的高度.
21. 如图,某校攀岩墙的顶部A处安装了一根安全绳 , 让它垂到地面时比墙高多出了2米,教练把绳子的下端C拉开8米后,发现其下端刚好接触地面(即米), , 求攀岩墙的高度. 22. 如图,是张大爷的一块小菜地,已知CD是中AB边上的高, , 求BD的长.(结果保留根号)
22. 如图,是张大爷的一块小菜地,已知CD是中AB边上的高, , 求BD的长.(结果保留根号) 23. 如图,在中, , , , 是的垂直平分线,分别交 , 于点 , .
23. 如图,在中, , , , 是的垂直平分线,分别交 , 于点 , . (1)、求证:是直角三角形;(2)、求的长.
(1)、求证:是直角三角形;(2)、求的长.