2023年浙教版数学七年级上册2.6 有理数的混合运算同步测试（提高版）

试卷更新日期：2023-08-03 类型：同步测试

进入出卷网下载

一、选择题（每题2分，共20分）

1. 按如图所示的运算程序，若输入m的值是-2，则输出的结果是（）

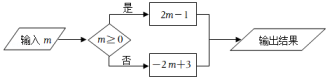A、-1 B、3 C、-5 D、7

查看试题解析
2. 某市星期一到星期五的每日最高气温与最低气温的变化趋势图如图，根据图中信息，下列说法正确的是（）

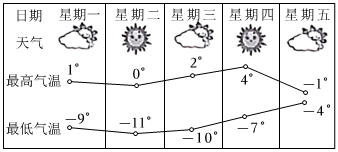A、星期一的日温差最大 B、星期三的日温差最小 C、星期二与星期四的日温差相同 D、星期一的日温差是星期五日温差的 $2$ 倍

查看试题解析
3. 如果 $a ， b$ 互为相反数， $x ， y$ 互为倒数，m是最大的负整数，则 $2023 (a + b) + 3 | m | - 3 x y$ 的值是（）

A、 $- 2$ B、 $- 1$ C、0 D、1

查看试题解析
4. 下列计算正确的是（）

A、 $8 \div (4 + 2) = 8 \div 4 + 8 \div 2 = 6$ B、 $(- 1) \div (- 2) \times \frac{1}{2} = (- 1) \div (- 1) = 1$ C、 $[- 2 - (+ 2)] \div 4 = 0 \div 4 = 0$ D、 $(+ 7) \times (- \frac{16}{5}) - 12 \times (- \frac{16}{5}) = (- \frac{16}{5}) \times (7 - 12) = (- \frac{16}{5}) \times (- 5) = 16$

查看试题解析
5. 在式子“ ${(- 2)}^{3} □ 5$ ”中的□里，填入下列哪种运算符号，使运算结果最大．

A、＋ B、－ C、× D、÷

查看试题解析
6. 如果四个互不相同的正整数 $m$ ， $n$ ， $p$ ， $q$ 满足 $(4 - m) (4 - n) (4 - p) (4 - q) = 4$ ，则 $4 m + 3 n + 2 p + q$ 的最大值为（）

A、47 B、48 C、49 D、50

查看试题解析
7. 若 $(\frac{1}{2} + \frac{1}{3} + \frac{1}{7} - \frac{1}{5}) \div 163 = \frac{1}{210}$ ，则计算 $90 - 163 \div (\frac{1}{2} + \frac{1}{3} + \frac{1}{7} - \frac{1}{5})$ 的结果是（）

A、-120 B、120 C、-300 D、300

查看试题解析
8. 按《航空障碍灯（MH/T6012-2015）》的要求，为保障飞行器夜间飞行的安全，在高度为45米至105米的建筑上必须安装中光强航空障碍灯（AviationObstructionlight），中光强航空障碍灯闪光频率不低于每分钟20次，不高于每分钟70次，下图是某一种中光强航空障碍灯的闪光模式，灯的亮暗呈规律性交替变化，那么在一个连续的10秒内，该航空障碍灯处于亮的状态时间总和最长可达：（）

A、6.5秒 B、7秒 C、7.5秒 D、13秒

查看试题解析
9. 正整数中各位数字的立方和与其本身相等的数称为“水仙花数”、例如153， $1^{3} + 5^{3} + 3^{3} = 153$ ，因此“153”为“水仙花数”，则下列各数中： $① 370 ， ② 371 ， ③ 407 ， ④ 502$ ， “水仙花数”的个数是（）

A、1 B、2 C、3 D、4-

查看试题解析
10. 将2019减去它的 $\frac{1}{2}$ ，再减去余下的 $\frac{1}{3}$ ，再减去余下的 $\frac{1}{4}$ ，最后减去余下的 $\frac{1}{2019}$ ，则最后的差是（）

A、 $\frac{1}{2019}$ B、 $\frac{2018}{2019}$ C、 ${(\frac{2018}{2019})}^{2}$ D、1

查看试题解析

二、填空题（每空2分，共16分）

11. 因疫情防控需要，一辆货车在早上8：00从甲地出发运送防疫物资到距离 $330 k m$ 乙地， $t (h)$ 后货车到达离甲地 $90 k m$ 的服务区休息，此时一辆轿车正从甲地急送防疫专家到乙地.10：00货车以原来的速度继续行驶，11：00轿车在距离甲地 $150 k m$ 处追上了货车，两车继续向乙地行驶.

(1)、货车的速度是 $k m / h$ .

(2)、轿车比货车早 $h$ 到达乙地.

查看试题解析
12. 整数a、b、c满足1000|a|+10|b|+|c|=2023，其中|a|>1且abc>1，则a+b+c的最小值是．

查看试题解析
13. 黑板上写着7个数，分别为： $- 8$ ， a，1，13，b，0， $- 6$ ，它们的和为 $- 10$ ，若每次从中任意擦除两个数，同时写上一个新数（新数为所擦除的两个数的和加上1），这样操作若干次，直至黑板上只剩下一个数，则所剩的这个数是．

查看试题解析
14. 某食品厂从生产的袋装食品中抽出样品10袋，检测每袋的质量是否符合标准，超过或不足的部分用正数或负数来表示，记录如下表：
与标准质量的差值/g
$- 1$
$- 2$
0
1
2
3
袋数
1
3
2
1
2
1
若每袋标准质量为 $200 g$ ，则抽样检测的总质量为 $g$ ．

查看试题解析
15. 我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳记数”.如图一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数，如图1，孩子出生后的天数＝3×7²＋2×7¹＋6＝147＋14＋6＝167（天）.请根据图2，计算孩子自出生后的天数是天.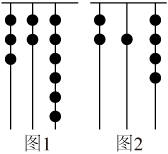

查看试题解析
16. 在算式 $3 - | - 2 □ 4 |$ 中的“□”里，填入运算符号“ $+$ ”，则算式的值为；在“□”里，填入运算符号（在符号“ $+$ ”“ $-$ ”“ $\times$ ”“ $\div$ ”中选择一个），可使算式的值最大．

查看试题解析

三、计算题（共27分）

17. 计算

(1)、 $5 \times (- 3) + (- 12) \times (- \frac{3}{4}) - \frac{5}{2}$

(2)、 $(- 48) × (\frac{5}{6} - 1 + \frac{7}{12} - \frac{1}{8})$

(3)、 $[{(- 1)}^{2023} + {(- 3)}^{2} × (\frac{1}{3} - \frac{1}{2})] × \frac{3}{10} ÷ (- 0 . 1^{2})$

查看试题解析
18. 计算：

(1)、 $2 - (- 4) + 8 \div (- 2) + (- 3)$ ；

(2)、 $- 3^{2} ÷ {(- 2)}^{2} × | - 1 \frac{1}{3} | \times 6 + {(- 2)}^{3}$ ；

(3)、 $25 \times \frac{3}{4} - (- 25) \times \frac{1}{2} + 25 \times (- \frac{1}{4})$ ；

(4)、 $99 \frac{71}{72} \times (- 36)$ .

查看试题解析
19. 计算：

(1)、 $- 66 \times 4 - (- 2.5) \div (- 0.1)$ ；

(2)、 $(\frac{1}{2} - \frac{1}{9} + \frac{1}{12}) \times 36$

查看试题解析

四、解答题（共10分）

20. 某种茶叶，若直接销售，每千克可获利润12元；若粗加工后销售，每千克可获利润50元；若精加工后销售，每千克可获利润75元．某茶叶加工厂现有这种茶叶140千克，该工厂的生产能力是：如果进行粗加工，每天可加工16千克；如果进行精加工，每天可加工6千克，但两种加工方式不能同时进行．受各种条件限制，工厂必须在15天内（含15天）将这批茶叶全部销售或加工完毕，为此该工厂营销科设计了三种方案：
方案一：全部进行粗加工；
方案二：15天全部进行精加工，没有来得及进行精加工的利润；
方案三：将60千克进行精加工，其余的进行粗加工．
你认为选择哪种方案可获利润最多，为什么？最多可获利润多少元？

查看试题解析
21. 请你仔细阅读下列材料：计算：
$(- \frac{1}{30}) \div (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5})$

解法 $1$ ：按常规方法计算

原式 $= (- \frac{1}{30}) \div [\frac{2}{3} + \frac{1}{6} - (\frac{1}{10} + \frac{2}{5})] = (- \frac{1}{30}) \div (\frac{5}{6} - \frac{1}{2}) = (- \frac{1}{30}) \times 3 = - \frac{1}{10}$

解法 $2$ ：简便计算，先求其倒数

原式的倒数为： $(\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5}) \div (- \frac{1}{30}) = (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5}) \times (- 30) = - 20 + 3 - 5 + 12 = - 10$

故 $(- \frac{1}{30}) \div (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5}) = - \frac{1}{10}$

再根据你对所提供材料的理解，模仿以上两种方法分别进行计算： $(- \frac{1}{56}) \div (\frac{3}{8} - \frac{3}{14} + \frac{1}{2} - \frac{2}{7})$

查看试题解析
22. 东方滴滴快车司机张师傅某天上午在东西走向的大街上连续接到六位客人（假设第一位客人下车后刚好第二位客人上车，以此类推），如果规定向东为正，向西为负，他这天上午行车里程（单位：千米）如下：-2，+10，-2，+8，-17，-3.

(1)、将最后一位乘客送到目的地时，张师傅距出发地多远？此时在出发地东边还是西边？

(2)、若汽车耗油量为0.1升/千米，这天上午张师傅共耗油多少升？

(3)、若滴滴快车的起步价为10元，起步里程为3千米（包括3千米），超过部分每米2元，请问张师傅这天上午收入多少元？

查看试题解析

23. 周至猕猴桃是西安的特产，质地柔软，口感香甜，当前网络销售日益盛行，陕西某主播为了助农增收，在其直播间直播销售周至猕猴桃，计划每天销售10000千克，但实际每天的销售量与计划量相比有增减，超过计划量记为正，不足计划量记为负.如表是该主播在直播带货期间第一周销售猕猴桃的情况：

星期	一	二	三	四	五	六	日
猕猴桃销售情况（单位：千克）	+400	-300	-200	+100	-600	+1100	+500

(1)、该主播在直播带货期间第一周销售猕猴桃最多的一天比最少的一天多销售多少千克？

(2)、与该主播在直播带货期间第一周计划总量相比，猕猴桃总销量超过或不足多少千克？

(3)、若该主播在直播期间按5元/千克进行猕猴桃销售，平均快递运费及其它费用为1元/千克，则该主播第一周直播带货销售猕猴桃为当地农民一共创收多少元？

查看试题解析

24. 2019年2月，市城区公交车施行全程免费乘坐政策，标志着我市公共交通建设迈进了一个新的时代．如图为某一条东西方向直线上的公交线路，东起职教园区站，西至富士康站，途中共设12个上下车站点，如图所示：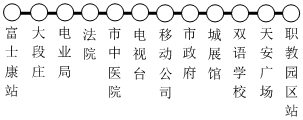

某天，小王从电业局站出发，始终在该线路的公交站点做志愿者服务，到 $A$ 站下车时，本次志愿者服务活动结束，如果规定向东为正，向西为负，当天的乘车站数按先后顺序依次记录如下 $($ 单位：站 $)$ ：+5，-2，+6，-11，+8﹐+1，-3，-2，-4，+7

(1)、请通过计算说明 $A$ 站是哪一站？

(2)、若相邻两站之间的平均距离为1.2千米，求这次小王志愿服务期间乘坐公交车行进的总路程是多少千米？

查看试题解析

与标准质量的差值/g	$- 1$	$- 2$	0	1	2	3
袋数	1	3	2	1	2	1

2023年浙教版数学七年级上册2.6 有理数的混合运算 同步测试（提高版）

一、选择题（每题2分，共20分）

二、填空题（每空2分，共16分）

三、计算题（共27分）

四、解答题（共10分）

2023年浙教版数学七年级上册2.6 有理数的混合运算同步测试（提高版）