【备考2024】浙江杭州数学中考十年回顾——函数
试卷更新日期:2023-08-03 类型:二轮复习
一、单选题
-
1. 在直角坐标系中,把点先向右平移1个单位,再向上平移3个单位得到点 . 若点的横坐标和纵坐标相等,则( )A、2 B、3 C、4 D、52. 设二次函数是实数 , 则( )A、当时,函数的最小值为 B、当时,函数的最小值为 C、当时,函数的最小值为 D、当时,函数的最小值为3. 如图,在平面直角坐标系中,已知点P(0,2),点A(4,2).以点P为旋转中心,把点A按逆时针方向旋转60°,得点B.在M1( ,0),M2( ,-1),M3(1,4),M4(2, )四个点中,直线PB经过的点是( )
 A、M1 B、M2 C、M3 D、M44. 在“探索函数 的系数 , , 与图象的关系”活动中,老师给出了直角坐标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).同学们探索了经过这四个点中的三个点的二次函数图象,发现这些图象对应的函数表达式各不相同,其中 的值最大为( )
A、M1 B、M2 C、M3 D、M44. 在“探索函数 的系数 , , 与图象的关系”活动中,老师给出了直角坐标系中的四个点:A(0,2),B(1,0),C(3,1),D(2,3).同学们探索了经过这四个点中的三个点的二次函数图象,发现这些图象对应的函数表达式各不相同,其中 的值最大为( ) A、 B、 C、 D、5. 已知 和 均是以 为自变量的函数,当 时,函数值分别是 和 ,若存在实数 ,使得 ,则称函数 和 具有性质P。以下函数 和 具有性质P的是( )A、 和 B、 和 C、 和 D、 和6. 在平面直角坐标系中,已知函数y=ax+a(a≠0)的图像经过点p(1,2),则该函数的图象可能是( )A、
A、 B、 C、 D、5. 已知 和 均是以 为自变量的函数,当 时,函数值分别是 和 ,若存在实数 ,使得 ,则称函数 和 具有性质P。以下函数 和 具有性质P的是( )A、 和 B、 和 C、 和 D、 和6. 在平面直角坐标系中,已知函数y=ax+a(a≠0)的图像经过点p(1,2),则该函数的图象可能是( )A、 B、
B、 C、
C、 D、
D、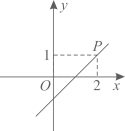 7. 设函数y=a(x-h)2+k(a,h,k是实数,a≠0),当x=1时,y=1,当x=8时,y=8,( )A、若h=4,则a<0 B、若h=5,则a>0 C、若h=6,则a<0 D、若h=7,则a>08. 在平面直角坐标系中,已知函数y1=x2+ax+1,y2=x2+bx+2,y3=x2+cx+4,其中a,b,c是正实数,且满足b2=ac。设函数y1 , y2 , y3的图象与x轴的交点个数分别为M1 , M2 , M3 , ( )A、若M1=2,M2=2,则M3=0 B、若M1=1,M2=0,则M3=0 C、若M1=0,M2=2,则M3=0 D、若M1=0,M2=0,则M3=09. 在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则( )A、m=3,n=2 B、m=-3,n=2 C、m=3,n=2 B.m=-2,n=310. 已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )A、
7. 设函数y=a(x-h)2+k(a,h,k是实数,a≠0),当x=1时,y=1,当x=8时,y=8,( )A、若h=4,则a<0 B、若h=5,则a>0 C、若h=6,则a<0 D、若h=7,则a>08. 在平面直角坐标系中,已知函数y1=x2+ax+1,y2=x2+bx+2,y3=x2+cx+4,其中a,b,c是正实数,且满足b2=ac。设函数y1 , y2 , y3的图象与x轴的交点个数分别为M1 , M2 , M3 , ( )A、若M1=2,M2=2,则M3=0 B、若M1=1,M2=0,则M3=0 C、若M1=0,M2=2,则M3=0 D、若M1=0,M2=0,则M3=09. 在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则( )A、m=3,n=2 B、m=-3,n=2 C、m=3,n=2 B.m=-2,n=310. 已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )A、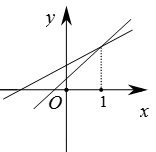 B、
B、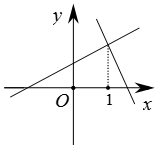 C、
C、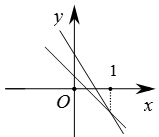 D、
D、 11. 在平面直角坐标系中,已知a≠b,设函数y=(x+a)(x+b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图象与x轴有N个交点,则( )A、M=N-1或M=N+1 B、M=N-1或M=N+2 C、M=N或M=N+1 D、M=N或M=N-112. 四位同学在研究函数 (b,c是常数)时,甲发现当 时,函数有最小值;乙发现 是方程 的一个根;丙发现函数的最小值为3;丁发现当 时, .已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
11. 在平面直角坐标系中,已知a≠b,设函数y=(x+a)(x+b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图象与x轴有N个交点,则( )A、M=N-1或M=N+1 B、M=N-1或M=N+2 C、M=N或M=N+1 D、M=N或M=N-112. 四位同学在研究函数 (b,c是常数)时,甲发现当 时,函数有最小值;乙发现 是方程 的一个根;丙发现函数的最小值为3;丁发现当 时, .已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A、甲 B、乙 C、丙 D、丁13. 设直线x=1是函数y=ax2+bx+c(a,b,c是实数,且a<0)的图象的对称轴,( )A、若m>1,则(m﹣1)a+b>0 B、若m>1,则(m﹣1)a+b<0 C、若m<1,则(m﹣1)a+b>0 D、若m<1,则(m﹣1)a+b<014. 设函数y= (k≠0,x>0)的图象如图所示,若z= ,则z关于x的函数图象可能为( )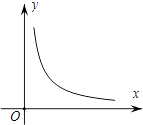 A、
A、 B、
B、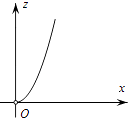 C、
C、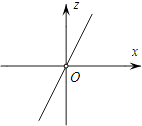 D、
D、 15. 设二次函数y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1 , 0),若函数y=y1+y2的图象与x轴仅有一个交点,则( )A、a(x1﹣x2)=d B、a(x2﹣x1)=d C、a(x1﹣x2)2=d D、a(x1+x2)2=d16. 函数的自变量x满足 ≤x≤2时,函数值y满足 ≤y≤1,则这个函数可以是( )A、y= B、y= C、y= D、y=
15. 设二次函数y1=a(x﹣x1)(x﹣x2)(a≠0,x1≠x2)的图象与一次函数y2=dx+e(d≠0)的图象交于点(x1 , 0),若函数y=y1+y2的图象与x轴仅有一个交点,则( )A、a(x1﹣x2)=d B、a(x2﹣x1)=d C、a(x1﹣x2)2=d D、a(x1+x2)2=d16. 函数的自变量x满足 ≤x≤2时,函数值y满足 ≤y≤1,则这个函数可以是( )A、y= B、y= C、y= D、y=二、填空题
-
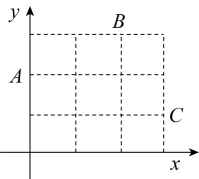
17. 在“探索一次函数y=kx+b的系数k、b与图象的关系”活动中,老师给出了直角坐标系中的三个点:A(0,2),B(2,3),C(3,1).同学们画出了经过这三个点中每两个点的一次函数的图象,并得到对应的函数表达式 . 分别计算 , 的值,其中最大的值等于 .
 18. 已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),则方程组 的解是19. 如图,在直角坐标系中,以点A(3,1)为端点的四条射线AB,AC,AD,AE分别过点B(1,1),点C(1,3),点D(4,4),点E(5,2),则∠BAC∠DAE(填“>”、“=”、“<”中的一个)
18. 已知一次函数y=3x-1与y=kx(k是常数,k≠0)的图象的交点坐标是(1,2),则方程组 的解是19. 如图,在直角坐标系中,以点A(3,1)为端点的四条射线AB,AC,AD,AE分别过点B(1,1),点C(1,3),点D(4,4),点E(5,2),则∠BAC∠DAE(填“>”、“=”、“<”中的一个)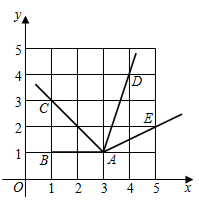 20. 某函数满足当自变量x=1时,函数值y=0;当自变量x=0时,函数值y=1.写出一个满足条件的函数表达式.21. 某日上午,甲、乙两车先后从A地出发沿一条公路匀速前往B地,甲车8点出发,如图是其行驶路程s(千米)随行驶时间t(小时)变化的图象.乙车9点出发,若要在10点至11点之间(含10点和11点)追上甲车,则乙车的速度v(单位:千米/小时)的范围是。
20. 某函数满足当自变量x=1时,函数值y=0;当自变量x=0时,函数值y=1.写出一个满足条件的函数表达式.21. 某日上午,甲、乙两车先后从A地出发沿一条公路匀速前往B地,甲车8点出发,如图是其行驶路程s(千米)随行驶时间t(小时)变化的图象.乙车9点出发,若要在10点至11点之间(含10点和11点)追上甲车,则乙车的速度v(单位:千米/小时)的范围是。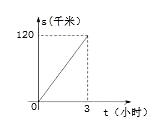 22. 在平面直角坐标系中,已知A(2,3),B(0,1),C(3,1),若线段AC与BD互相平分,则点D关于坐标原点的对称点的坐标为 .23. 函数y=x2+2x+1,当y=0时,x=;当1<x<2时,y随x的增大而(填写“增大”或“减小”).24. 在平面直角坐标系中,O为坐标原点,设点P(1,t)在反比例函数y= 的图象上,过点P作直线l与x轴平行,点Q在直线l上,满足QP=OP.若反比例函数y= 的图象经过点Q,则k= .25. 设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数解析式为 .
22. 在平面直角坐标系中,已知A(2,3),B(0,1),C(3,1),若线段AC与BD互相平分,则点D关于坐标原点的对称点的坐标为 .23. 函数y=x2+2x+1,当y=0时,x=;当1<x<2时,y随x的增大而(填写“增大”或“减小”).24. 在平面直角坐标系中,O为坐标原点,设点P(1,t)在反比例函数y= 的图象上,过点P作直线l与x轴平行,点Q在直线l上,满足QP=OP.若反比例函数y= 的图象经过点Q,则k= .25. 设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数解析式为 .三、综合题
-
26. 在直角坐标系中,已知 , 设函数与函数的图象交于点和点 . 已知点的横坐标是2,点的纵坐标是 .
 (1)、求的值.(2)、过点作轴的垂线,过点作轴的垂线,在第二象限交于点;过点作轴的垂线,过点作轴的垂线,在第四象限交于点 . 求证:直线经过原点.27. 设二次函数 , ( , 是实数).已知函数值和自变量的部分对应取值如下表所示:
(1)、求的值.(2)、过点作轴的垂线,过点作轴的垂线,在第二象限交于点;过点作轴的垂线,过点作轴的垂线,在第四象限交于点 . 求证:直线经过原点.27. 设二次函数 , ( , 是实数).已知函数值和自变量的部分对应取值如下表所示:…
0
1
2
3
…
…
1
1
…
(1)、若 , 求二次函数的表达式;(2)、写出一个符合条件的的取值范围,使得随的增大而减小.(3)、若在m、n、p这三个实数中,只有一个是正数,求的取值范围.28. 设函数y1= ,函数y2=k2x+b(k1 , k2 , b是常数,k1≠0,k2≠0).(1)、若函数y1和函数y2的图象交于点A(1,m),点B(3,1),①求函数y1 , y2的表达式:
②当2<x<3时,比较y1与y2的大小(直接写出结果).
(2)、若点C(2,n)在函数y1的图象上,点C先向下平移2个单位,再向左平移4个单位,得点D,点D恰好落在函数y1的图象上,求n的值,29. 设二次函数y1=2x2+bx+c(b,c是常数)的图象与x轴交于A,B两点.(1)、若A,B两点的坐标分别为(1,0),(2,0),求函数y)的表达式及其图象的对称轴.(2)、若函数y1的表达式可以写成心=2(x-h)2-2(h是常数)的形式,求b+c的最小值.(3)、设一次函数y2=x-m(m是常数),若函数y1的表达式还可以写成y1=2(x-m)(x-m-2)的形式,当函数y=y1-y2的图象经过点(x0 , 0)时,求x0-m的值.30. 在直角坐标系中,设函数 ( 是常数, , )与函数 ( 是常数, )的图象交于点A,点A关于 轴的对称点为点B。 (1)、若点B的坐标为(-1,2),
(1)、若点B的坐标为(-1,2),①求 , 的值; ②当 时,直接写出 的取值范围;
(2)、若点B在函数 ( 是常数, )的图象上,求 的值。31. 在直角坐标系中,设函数 ( , 是常数, )。(1)、若该函数的图象经过(1,0)和(2,1)两点,求函数的表达式,并写出函数图象的顶点坐标;(2)、写出一组a、b的值,使函数y=ax2+bx+1的图象与x轴有两个不同的交点,并说明理由.(3)、已知 ,当 , ( , 是实数, )时,该函数对应的函数值分别为P,Q。若 ,求证:P+Q>6 。32. 设函数y1= ,y2=- (k>0)。(1)、当2≤x≤3时,函数y1的最大值是a,函数y2的最小值是a-4,求a和k的值。(2)、设m≠0,且m≠-1,当x=m时,y1=p;当x=m+1时,y1=q。圆圆说:“p一定大于q”。你认为圆圆的说法正确吗?为什么?33. 在平面直角坐标系中,设二次函数y1=x2+bx+a,y2=ax2+bx+1(a,b是实数,a≠0)。(1)、若函数y1的对称轴为直线x=3,且函数y1的图象经过点(a,b),求函数y1的表达式。(2)、若函数y1的图象经过点(r,0),其中r≠0,求证:函数y2的图象经过点( ,0)。(3)、若函数y1和函数y2的最小值分别为m和n,若m+n=0,求m,n的值。34. 方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480千米,设小汽车的行驶时间为t(单位:小时),行驶速度为(单位:千米/小时),且全程速度限定为不超过120千米/小时。(1)、求v关于t的函数表达式。(2)、方方上午8点驾驶小汽车从A地出发.①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
②方方能否在当天11点30分前到达B地?说明理由
35. 设二次函数y=(x-x1)(x-x2)(x1 , x2是实数)。(1)、甲求得当x=0时,y=0;当x=1时,y=0;乙求得当x= 时,y=- ,若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由.(2)、写出二次函数图象的对称轴,并求该函数的最小值(用含x1 , x2的代数式表示).(3)、已知二次函数的图象经过(0,m)和(1,n)两点(m.n是实数)当0<x1<x2<1时,求证:0<mn< .36. 已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货,设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时)。(1)、求v关于t的函数表达式(2)、若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?37. 设一次函数 ( 是常数, )的图象过A(1,3),B(-1,-1)
(1)、求该一次函数的表达式;(2)、若点(2a+2,a2)在该一次函数图象上,求a的值;(3)、已知点C(x1 , y1),D(x2 , y2)在该一次函数图象上,设m=(x1-x2)(y1-y2),判断反比例函数 的图象所在的象限,说明理由。38. 设二次函数 (a,b是常数,a≠0)(1)、判断该二次函数图象与x轴交点的个数,说明理由.(2)、若该二次函数的图象经过A(-1,4),B(0,-1),C(1,1)三个点中的其中两个点,求该二次函数的表达式;(3)、若a+b<0,点P(2,m)(m>0)在该二次函数图象上,求证:a>0.39. 在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).(1)、当﹣2<x≤3时,求y的取值范围;(2)、已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.40. 在面积都相等的所有矩形中,当其中一个矩形的一边长为1时,它的另一边长为3.(1)、设矩形的相邻两边长分别为x,y.①求y关于x的函数表达式;
②当y≥3时,求x的取值范围;
(2)、圆圆说其中有一个矩形的周长为6,方方说有一个矩形的周长为10,你认为圆圆和方方的说法对吗?为什么?41. 在平面直角坐标系中,设二次函数y1=(x+a)(x﹣a﹣1),其中a≠0.(1)、若函数y1的图象经过点(1,﹣2),求函数y1的表达式;(2)、若一次函数y2=ax+b的图象与y1的图象经过x轴上同一点,探究实数a,b满足的关系式;(3)、已知点P(x0 , m)和Q(1,n)在函数y1的图象上,若m<n,求x0的取值范围.42. 把一个足球垂直水平地面向上踢,时间为t(秒)时该足球距离地面的高度h(米)适用公式h=20t﹣5t2(0≤t≤4).(1)、当t=3时,求足球距离地面的高度;(2)、当足球距离地面的高度为10米时,求t;(3)、若存在实数t1 , t2(t1≠t2)当t=t1或t2时,足球距离地面的高度都为m(米),求m的取值范围.43. 已知函数y1=ax2+bx,y2=ax+b(ab≠0).在同一平面直角坐标系中.(1)、若函数y1的图象过点(﹣1,0),函数y2的图象过点(1,2),求a,b的值.(2)、若函数y2的图象经过y1的顶点.①求证:2a+b=0;
②当1<x< 时,比较y1 , y2的大小.
44. 设函数y=(x﹣1)[(k﹣1)x+(k﹣3)](k是常数). (1)、当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时的函数的图象;(2)、根据图象,写出你发现的一条结论;(3)、将函数y2的图象向左平移4个单位,再向下平移2个单位,得到的函数y3的图象,求函数y3的最小值.45. 方成同学看到一则材料:甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地.设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示.
(1)、当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时的函数的图象;(2)、根据图象,写出你发现的一条结论;(3)、将函数y2的图象向左平移4个单位,再向下平移2个单位,得到的函数y3的图象,求函数y3的最小值.45. 方成同学看到一则材料:甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地.设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示.方成思考后发现了如图1的部分正确信息:乙先出发1h;甲出发0.5小时与乙相遇.
请你帮助方成同学解决以下问题:
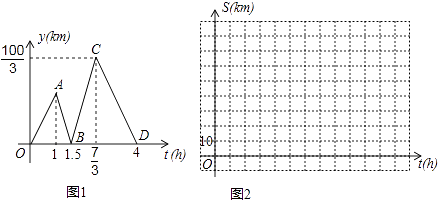 (1)、分别求出线段BC,CD所在直线的函数表达式;(2)、当20<y<30时,求t的取值范围;(3)、分别求出甲,乙行驶的路程S甲 , S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象;(4)、丙骑摩托车与乙同时出发,从N地沿同一公路匀速前往M地,若丙经过 h与乙相遇,问丙出发后多少时间与甲相遇?46. 在直角坐标系中,设x轴为直线l,函数y=﹣ x,y= x的图象分别是直线l1 , l2 , 圆P(以点P为圆心,1为半径)与直线l,l1 , l2中的两条相切.例如( ,1)是其中一个圆P的圆心坐标.
(1)、分别求出线段BC,CD所在直线的函数表达式;(2)、当20<y<30时,求t的取值范围;(3)、分别求出甲,乙行驶的路程S甲 , S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象;(4)、丙骑摩托车与乙同时出发,从N地沿同一公路匀速前往M地,若丙经过 h与乙相遇,问丙出发后多少时间与甲相遇?46. 在直角坐标系中,设x轴为直线l,函数y=﹣ x,y= x的图象分别是直线l1 , l2 , 圆P(以点P为圆心,1为半径)与直线l,l1 , l2中的两条相切.例如( ,1)是其中一个圆P的圆心坐标.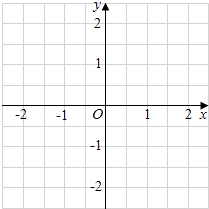 (1)、写出其余满足条件的圆P的圆心坐标;(2)、在图中标出所有圆心,并用线段依次连接各圆心,求所得几何图形的周长.
(1)、写出其余满足条件的圆P的圆心坐标;(2)、在图中标出所有圆心,并用线段依次连接各圆心,求所得几何图形的周长.四、解答题
-
47. 复习课中,教师给出关于x的函数y=2kx2﹣(4k+1)x﹣k+1(k是实数).
教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写到黑板上.
学生思考后,黑板上出现了一些结论.教师作为活动一员,又补充一些结论,并从中选出以下四条:
①存在函数,其图象经过(1,0)点;
②函数图象与坐标轴总有三个不同的交点;
③当x>1时,不是y随x的增大而增大就是y随x的增大而减小;
④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数.
教师:请你分别判断四条结论的真假,并给出理由.最后简单写出解决问题时所用的数学方法.