广东省清远市2022-2023学年八年级下学期数学期末试卷
试卷更新日期:2023-08-03 类型:期末考试
一、选择题(本大题10小题,每小题3分,共30分)
-
1. 窗棂即窗格(窗里面的横的、竖的或斜的格)是中国传统木构建筑的框架结构设计,窗棂上雕刻有线槽和各种化纹,构成种类繁多的优美图案,下列表示我国古代窗棂样式结构图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在中, , 则的度数是( )A、 B、 C、 D、3. 如图,A,B两点分别位于一个池塘的两端,小峰想用绳子测量A,B间的距离,但绳子不够长,小红同学帮他想了一个主意,先在地上取一个可以直接到达A,B的点 , 找到AC,BC的中点D,E,并且测出DE的长为 , 则A,B两点的距离为( )
2. 在中, , 则的度数是( )A、 B、 C、 D、3. 如图,A,B两点分别位于一个池塘的两端,小峰想用绳子测量A,B间的距离,但绳子不够长,小红同学帮他想了一个主意,先在地上取一个可以直接到达A,B的点 , 找到AC,BC的中点D,E,并且测出DE的长为 , 则A,B两点的距离为( ) A、 B、 C、 D、4. 如图,平行四边形ABCD的对角线AC、BD交于点 , 下列结论错误的是( )
A、 B、 C、 D、4. 如图,平行四边形ABCD的对角线AC、BD交于点 , 下列结论错误的是( ) A、 B、 C、 D、5. 正五边形的外角和为( )A、 B、 C、 D、6. 点 , 若将线段AB平移到线段CD,使点到达点 , 则点的坐标是( )A、 B、 C、 D、7. 不等式的正整数解是( )A、 B、 C、 D、8. 如图,四边形ABCD经过旋转后与四边形ADEF重合,下面说法中不一定正确的( )
A、 B、 C、 D、5. 正五边形的外角和为( )A、 B、 C、 D、6. 点 , 若将线段AB平移到线段CD,使点到达点 , 则点的坐标是( )A、 B、 C、 D、7. 不等式的正整数解是( )A、 B、 C、 D、8. 如图,四边形ABCD经过旋转后与四边形ADEF重合,下面说法中不一定正确的( ) A、点A是旋转中心 B、 C、 D、9. 《九章算术》中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到900里远的城市,所需时间比规定时间多1天;若改为快马派送,则所需时间比规定时间少3天,已知快马的速度是慢马速度的2倍,求规定时间,设规定时间为天,则可列出正确的方程为( )A、 B、 C、 D、10. 如图所示,一次函数是常数与正比例函数是常数,的图像相交于点 , 下列判断错误的是( )
A、点A是旋转中心 B、 C、 D、9. 《九章算术》中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到900里远的城市,所需时间比规定时间多1天;若改为快马派送,则所需时间比规定时间少3天,已知快马的速度是慢马速度的2倍,求规定时间,设规定时间为天,则可列出正确的方程为( )A、 B、 C、 D、10. 如图所示,一次函数是常数与正比例函数是常数,的图像相交于点 , 下列判断错误的是( ) A、关于的方程的解是 B、关于的不等式的解集是 C、关于x,y的方程组的解是 D、当时,对应的函数值比的函数值大.
A、关于的方程的解是 B、关于的不等式的解集是 C、关于x,y的方程组的解是 D、当时,对应的函数值比的函数值大.二、填空题(本大题共5小题,每小题3分,共15分)
-
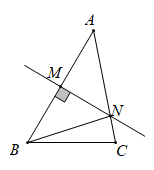
11. 因式分解: .12. 计算:.13. 如图,在 中, ,线段 的垂直平分线交 于点 , ,则 的长为.
 14. 用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素含量如下表:
14. 用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素含量如下表:项目
甲种原料
乙种原料
维生素C含量(单位/千克)
600
100
现配制这种饮料10千克,要求至少含有4200单位的维生素C,若设所需甲种原料的质量为x千克,则x应满足的不等式为.
15. 如图,在平行四边形ABCD中,AB=2,BC=3,∠B=60°,点P在AD上,且AP=2,CP⊥AD,若直线经过点P,将该平行四边形的面积平分,并与平行四边形的另一边交于点Q,则线段PQ的长度为.

三、解答题(一)(共3小题,每小题8分,共24分)
-
16. 解分式方程:.17. 将下面证明中每一步的理由写在括号内.

如图,有两个长度相等的滑梯BC与EF,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,求证:.
证明: ,
, (已知)
RtRt ).
).
( ).
.( ).
18. 尺规作图(不要求写作法):如图,点分别在直线上与直线外,求作直线 , 的垂线 , 使它经过点 , 作直线的垂线 , 使它经过点.
四、解答题(二)(共3小题,每小题9分,共27分)
-
19. 在如图所示的三角形纸片ABC中,.按如下步骤可以把这个直角三角形纸片分成三个全等的小直角三角形(图中虚线表示折痕);

①折叠三角形纸片ABC,使点与点重合;
②将折叠后的纸片再沿AD对折.
(1)、由步骤①可以得到哪些等量关系?(2)、请证明.20. 如图,在□中,对角线AC、BD相交于点O,E、F是对角线AC上的两点. (1)、现有四个等式:①AE=CF;②∠ADE=∠CBF;③DE=BF;④ .
(1)、现有四个等式:①AE=CF;②∠ADE=∠CBF;③DE=BF;④ .请从以上条件中选择一个添加,使四边形DEBF是平行四边形.你添加的是.(只填一个正确的序号)
(2)、利用(1)中你选择的条件,证明四边形DEBF为平行四边形.21. 三个数 , , 3在数轴上从左到右依次排列,求a的取值范围.五、解答题(三)(共2小题,每小题12分,共24分)
-
22. 观察下列式子:
①;
②;
③;
④.
(1)、填空:(填写“>”或“=”或“<”);(2)、观察以上各式,它们有什么规律吗?请用含a,b的式子表示你发现的规律,并说明该式成立;(3)、运用你发现的规律,请求出代数式的最小值.23. 已知:在Rt中, , 将绕点顺时针旋转一定的角度得到 , 点B、C的对应点分别是E、D. (1)、如图1,若α=60°时,连接BE,求证:AB=BE;(2)、如图2,当点E恰好在AC上时,求∠CDE的度数;(3)、如图3,BC=1,点Q是线段AC上的一个动点,点M是线段AB上的一个动点,是否存在这样的点Q、M使得△CQM为等腰三角形且△AQM为直角三角形?若存在,请求出满足条件的BM的长;若不存在,请说明理由.
(1)、如图1,若α=60°时,连接BE,求证:AB=BE;(2)、如图2,当点E恰好在AC上时,求∠CDE的度数;(3)、如图3,BC=1,点Q是线段AC上的一个动点,点M是线段AB上的一个动点,是否存在这样的点Q、M使得△CQM为等腰三角形且△AQM为直角三角形?若存在,请求出满足条件的BM的长;若不存在,请说明理由.