广东省惠州市惠东县2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-03 类型：期末考试

进入出卷网下载

一、单选题

1. 下列根式是最简二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{\frac{1}{5}}$ C、 $\sqrt{5}$ D、 $\sqrt{8}$

查看试题解析
2. 下列四组线段中，可以组成直角三角形的是（）

A、4，5，6 B、1， $\sqrt{3}$ ， 2 C、5，6，7 D、1， $\sqrt{2}$ ， 3

查看试题解析
3. 如图， $▱ A B C D$ 的对角线 $A C$ 、 $B D$ 交于点O，则下列结论一定成立的是（）

A、 $O A = O C$ B、 $A B = O B$ C、 $A C = B D$ D、 $A C ⊥ B D$

查看试题解析
4. 一次函数 $y = - 5 x + 5$ 的图像经过的象限是（）

A、一、二、三 B、二、三、四 C、一、二、四 D、一、三、四

查看试题解析
5. 已知一组数据分别为 $3$ ， $8$ ， $4$ ， $5$ ， $x$ ，这组数据的众数是 $8$ ，则这组数据的中位数是（）

A、 $3$ B、 $4$ C、 $5$ D、 $8$

查看试题解析
6. 关于函数 $y = - 2 x + 1$ ，下列结论正确的是（）

A、图像经过点 $(- 2 ， 1)$ B、y随x的增大而增大 C、图像与y轴交点为 $(0 ， 1)$ D、图像不经过第一象限

查看试题解析
7. 如图，将正方形ABCD剪去4个全等的直角三角形（图中阴影部分），得到边长为c的四边形EFGH，下列等式成立的是（）

A、 $a + b = c$ B、 $c^{2} = (a + b)^{2} \cdot 4 a b$ C、 $c^{2} = (a + b) (a - b)$ D、 $a^{2} + b^{2} = c^{2}$

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， ∠ A = 30 °$ ， D，E，F分别为 $A B ， A C ， A D$ 的中点，若 $B C = 2 \sqrt{3}$ ，则 $E F$ 的长度为（）

A、1 B、2 C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析
9. 若一组数据 $a_{1}$ ， $a_{2}$ ， ……， $a_{n}$ 的平均数为 $10$ ，方差为 $4$ ，那么数据 $3 a_{1} - 2$ ， $3 a_{2} - 2$ ， …， $3 a_{n} - 2$ 的平均数和方差分别是（）

A、 $30$ ， $12$ B、 $28$ ， $10$ C、 $28$ ， $36$ D、 $28$ ， $34$

查看试题解析
10. 如图是一个按某种规律排列的数阵：根据数阵排列的规律，第n（n是整数，且n≥3）行从左向右数第（n﹣2）个数是（　　　）（用含n的代数式表示）

A、 $\sqrt{n^{2} - 1}$ B、 $\sqrt{n^{2} - 2}$ C、 $\sqrt{n^{2} - 3}$ D、 $\sqrt{n^{2} - 4}$

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{1 - x}$ 在实数范围有意义，则 $x$ 的取值范围是.

查看试题解析
12. 把一次函数 $y = - 2 x + 1$ 的图像沿 $y$ 轴向上平移 $4$ 个单位长度后，得到的新图像对应的函数解析式为．

查看试题解析
13. 如图，在菱形 $A B C D$ 中，对角线 $A C = 12$ ， $B D = 16$ ，则这个菱形的周长为．

查看试题解析
14. 如图，直线y=x+b与y=kx的图象交于点M(-5，5)，则不等式x+b>kx的解集为。

查看试题解析
15. 如图，在正方形 $A B C D$ 中，点 $E$ 是边 $A B$ 上一点，且 $A E = 2$ ， $B E = 4$ ，点 $P$ 是边 $A D$ 上的动点（ $P$ 与 $A$ ， $D$ 不重合），则 $P E + P C$ 的最小值是．

查看试题解析

三、解答题

16. 计算： $\sqrt{8} - 2 \sqrt{\frac{1}{2}} + (2 - \sqrt{3}) (2 + \sqrt{3})$ ．

查看试题解析
17. 21世纪已经进入了中国太空时代，2021年到2022年，我国会通过11次航天发射完成空间站建设，空间站有“天和”核心舱、“问天”和“梦天”两个实验舱，我国空间站的建成将为开展太空实验及更广泛的国际合作提供精彩舞台校团委以此为契机，组织了“中国梦，航天情”系列活动．下面是八年级甲、乙两个班各项目的成绩（单位：分）：
项目班次
知识竞赛
演讲比赛
版面创作
甲
85
91
88
乙
90
84
87

(1)、如果根据三项成绩的平均分计算最后成绩，请通过计算说明甲、乙两班谁将获胜；

(2)、如果将知识竞赛、演讲比赛、版面创作按5：3：2的比例确定最后成绩，请通过计算说明甲、乙两班谁将获胜．

查看试题解析
18. 已知一次函数 $y = k x + b$ 的图像经过点 $A (- 1 ， - 5)$ ，且与正比例函数 $y = \frac{1}{2} x$ 的图像相交于点 $B (2 ， a)$ ，

(1)、求点 $B$ 的坐标；

(2)、求一次函数解析式．

查看试题解析
19. 如图，在 $△ A B C$ 中，过点A作 $A D ⊥ B C$ 于点D，点E在线段 $B D$ 上，且 $E A = E B$ ．已知 $B D = 16$ ， $A D = 12$ ， $A C = 15$ ．

(1)、求线段 $D E$ 的长；

(2)、求证： $∠ B A C = 90 °$ ．

查看试题解析
20. 已知：四边形 $A B C D$ 是平行四边形，点 $E$ 为 $B C$ 边上一点，且 $A B = A E$ ，求证：

(1)、 $∠ B = ∠ D A E$ ；

(2)、 $A C = D E$ ．

查看试题解析
21. 如图：在菱形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 交于点 $O$ ，过点 $A$ 作 $A E ⊥ B C$ 于点 $E$ ，延长 $B C$ 至点 $F$ ，使 $C F = B E$ ，连接 $D F$ ．

(1)、求证：四边形 $A E F D$ 是矩形；

(2)、若 $B F = 16$ ， $D F = 8$ ，求菱形 $A B C D$ 的面积．

查看试题解析
22. 如图，在平面直角坐标系中，直线 $l_{1}$ 的解析式为 $y = x$ ，直线 $l_{2}$ 的解析式为 $y = - \frac{1}{2} x + 3$ ，与x轴、y轴分别交于点A、点B，直线 $l_{1}$ 与 $l_{2}$ 交于点C．

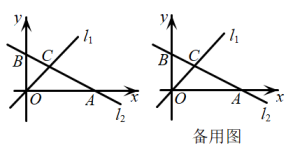(1)、求出点A、点B的坐标；

(2)、求 $△ C O B$ 的面积；

(3)、在x轴上是否存在一点P，使得 $△ P O C$ 为等腰三角形？若存在，请直接写出点P坐标，若不存在，请说明理由．

查看试题解析
23. 如图，矩形 $O A B C$ 的顶点 $A$ 、 $C$ 分别位于 $x$ 轴和 $y$ 轴的正半轴上，线段 $O A$ 、 $O C$ 的长度满足： $| O A - 15 | + \sqrt{O C - 9} = 0$ ，点 $N$ 在 $O C$ 上，将 $△ B C N$ 沿直线 $B N$ 折叠，点 $C$ 恰好落在 $x$ 轴上的点 $D$ 处，且 $O D = 3$ ．

(1)、求点 $B$ 的坐标；

(2)、求直线 $B N$ 的解析式；

(3)、坐标平面内是否存在一点 $P$ ，使以 $B$ 、 $N$ ， $D$ 、 $P$ 为顶点的四边形是平行四边形？若存在，请说明理由并求出点 $P$ 的坐标；若不存在，请说明理由．

查看试题解析

项目班次	知识竞赛	演讲比赛	版面创作
甲	85	91	88
乙	90	84	87