广东省广州市天河区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-03 类型:期末考试
一、单选题
-
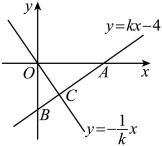
1. 若式子 在实数范围内有意义,则x的取值范围是( )A、x≤-3 B、x≥-3 C、x<-3 D、x>-32. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、3. 一组数据2,4,5,3,2的中位数是( )A、2 B、3 C、3.5 D、54. 在函数中,当自变量时,函数值等于( )A、1 B、4 C、7 D、135. 在平行四边形 , 若 , 则度数为( )A、 B、 C、 D、6. 在矩形中,对角线 , 交于点 , 若 , 则长为( )A、 B、 C、 D、7. 正比例函数的图象在第二、四象限,则一次函数的图象大致是( )A、
 B、
B、 C、
C、 D、
D、 8. 如图,点在正方形的内部,连接 , , 若 , , , 则正方形的面积是( )
8. 如图,点在正方形的内部,连接 , , 若 , , , 则正方形的面积是( ) A、 B、 C、 D、9. 下列条件中,不能判断是直角三角形的是( )A、三角形三条边的比为 B、三角形三条边满足关系式 C、三角形三条边的比为 D、三角形三个内角满足关系式
A、 B、 C、 D、9. 下列条件中,不能判断是直角三角形的是( )A、三角形三条边的比为 B、三角形三条边满足关系式 C、三角形三条边的比为 D、三角形三个内角满足关系式二、多选题
-
10. 如图,正方形的顶点A,B别在x轴、y轴上, , , 若的中点E好落在x轴上,此时恰好也垂直于y轴,交y轴于点F,连接 . 判断:①;②是等边三角形;③;④ . 其中正确的有( )
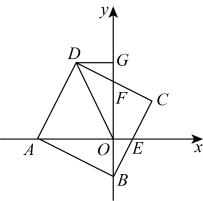 A、① B、② C、③ D、④
A、① B、② C、③ D、④三、填空题
-
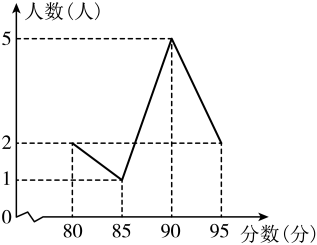
11. 计算的结果是 .12. 若函数的图象经过点 , 则k的值为 .13. 菱形的一边长为 , 则这个菱形的周长为 .14. 在演讲比赛中,10名选手的成绩统计图如图所示,则这10名选手成绩的众数是 .
 15. 如果平行四边形边 , 且的长是平行四边形周长的 , 则边的长为 .16. 定义:我们把三角形某边上高的长度与这边中点到高的距离的比值称为三角形某边的“中偏度值”.如图,中, , , , 是边上的高,则中边的“中偏度值”为 .
15. 如果平行四边形边 , 且的长是平行四边形周长的 , 则边的长为 .16. 定义:我们把三角形某边上高的长度与这边中点到高的距离的比值称为三角形某边的“中偏度值”.如图,中, , , , 是边上的高,则中边的“中偏度值”为 .
四、解答题
-
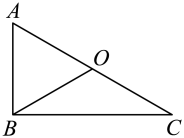
17. 计算:(1)、;(2)、18. 如图,中, , 是的中点,若 , 求的度数.
 19. 八年级的同学们即将步入初三,某校的一个主题班会小组为了解八年级900名同学对初三学习的第一印象,用问卷开展随机调查,共有50名同学参加了抽样调查(每人只能选一项),小组将所得数据统计如图所示,请你帮忙解决问题:
19. 八年级的同学们即将步入初三,某校的一个主题班会小组为了解八年级900名同学对初三学习的第一印象,用问卷开展随机调查,共有50名同学参加了抽样调查(每人只能选一项),小组将所得数据统计如图所示,请你帮忙解决问题: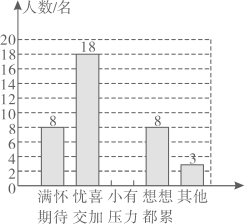 (1)、将统计图补充完整;并估计八年级全体同学对初三学习第一印象是“忧喜交加”的人数;(2)、结合统计数据,写一条发现的结论,并给出适当的建议.20. 如图,在四边形ABCD中, , , AC平分∠BAD.求证:四边形ABCD是菱形.
(1)、将统计图补充完整;并估计八年级全体同学对初三学习第一印象是“忧喜交加”的人数;(2)、结合统计数据,写一条发现的结论,并给出适当的建议.20. 如图,在四边形ABCD中, , , AC平分∠BAD.求证:四边形ABCD是菱形. 21. 已知y是x的一次函数,部分对应值如表所示.
21. 已知y是x的一次函数,部分对应值如表所示.x
0
2
n
y
3
m
(1)、求该一次函数的表达式;(2)、求的值.22. 甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.(1)、以x(单位:元)表示商品原价,y(单位:元)表示购物金额,分别就两家商场的让利方式写出y关于x的函数解析式;(2)、春节期间如何选择这两家商场去购物更省钱?
-