广东省广州市荔湾区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-03 类型:期末考试
一、单选题
-
1. 下列各组二次根式中,能进行合并的是( )A、与 B、与 C、与 D、与2. 下列说法中正确的个数有( )(1)想了解观众对某体育节目的喜爱程度,宜采用抽样调查;(2)某鞋店店主在进货时应关注销售鞋子尺码的平均数;(3)数据1,1,2,2,3的众数是3;(4)一组数据的波动越大,方差越小.A、1 B、2 C、3 D、43. 下列计算正确的是( )A、 B、 C、 D、4. 在平面直角坐标系中,将直线沿轴向下平移2个单位后恰好经过原点,则的值为( )A、 B、2 C、4 D、5. 如图,在四边形中,对角线、相交于点 , 下列条件不能判定四边形为平行四边形的是( )
 A、 B、 C、 D、6. 若 , 是一元二次方程的两个根,则的值是( )A、 B、 C、1 D、77. 已知关于的一元二次方程无实数根,则一次函数的图象不经过第( )象限.A、一 B、二 C、三 D、四8. 如图,▱ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
A、 B、 C、 D、6. 若 , 是一元二次方程的两个根,则的值是( )A、 B、 C、1 D、77. 已知关于的一元二次方程无实数根,则一次函数的图象不经过第( )象限.A、一 B、二 C、三 D、四8. 如图,▱ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )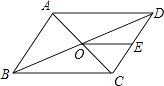 A、15 B、18 C、21 D、249. 时,一次函数的最大值为 , 则( )A、 B、 C、 D、10. 如图,正方形的边长为 , P为对角线上动点,过P作于E,于F,连接 , 则的最小值为( )
A、15 B、18 C、21 D、249. 时,一次函数的最大值为 , 则( )A、 B、 C、 D、10. 如图,正方形的边长为 , P为对角线上动点,过P作于E,于F,连接 , 则的最小值为( ) A、2 B、4 C、 D、1
A、2 B、4 C、 D、1二、填空题
-
11. 当时,二次根式有最小值.12. 已知一组数据7,1,5,4,8,则这组数据的方差是 .13. 对于任意的实数a,b,定义一种新运算: , 若 , 则的值为 .14. 在平面直角坐标系中,已知 , , 作的垂直平分线交轴于点 , 则点坐标为 .15. 如图,函数与的图象交于点 , 则不等式的解集为 .
 16. 如图, , 分别是正方形的边和的中点, , 连接 , , 取的中点 , 连接 , , 下列结论:①;②;③;④四边形的面积为;⑤ . 以上说法正确的有 .
16. 如图, , 分别是正方形的边和的中点, , 连接 , , 取的中点 , 连接 , , 下列结论:①;②;③;④四边形的面积为;⑤ . 以上说法正确的有 .
三、解答题
-
17. 解方程: .18. 如图,在中,对角线的垂直平分线分别交 , 于点 , , 点为垂足,连接 , . 求证:四边形是菱形.
 19. 计算:(1)、;(2)、 .20. 某学校两组学生参加知识竞赛,将他们的参赛成绩(单位:分)整理如下:
19. 计算:(1)、;(2)、 .20. 某学校两组学生参加知识竞赛,将他们的参赛成绩(单位:分)整理如下:甲组:6,6,9,7,9,10,9.
乙组:7,6,10,5,9,9,10.
分析数据,如图表:
平均数
中位数
众数
甲组
9
乙组
8
9
(1)、表中的 , ;;(2)、请说明乙组学生数据的“中位数9”的意义.21. 如图,有一块长为30米,宽为20米的矩形场地,计划在该场地上修建两条互相垂直的小道,横向小道与坚向小道的宽比为 , 余下矩形场地建成草坪,草坪的面积为486平方米,请求出横向小道的宽. 22. 在平面直角坐标系中,过点的直线交轴正半轴于点 , 已知 .(1)、求点的坐标;(2)、点是轴上一点,且的面积为4,求直线的解析式.23. 已知:如图, , , , 动点从点出发沿射线以的速度移动,设运动的时间为 .
22. 在平面直角坐标系中,过点的直线交轴正半轴于点 , 已知 .(1)、求点的坐标;(2)、点是轴上一点,且的面积为4,求直线的解析式.23. 已知:如图, , , , 动点从点出发沿射线以的速度移动,设运动的时间为 . (1)、请判断的形状,并说明理由;(2)、当为直角三角形时,求的值.24. 如图,直线分别与轴,轴交于 , 两点.
(1)、请判断的形状,并说明理由;(2)、当为直角三角形时,求的值.24. 如图,直线分别与轴,轴交于 , 两点. (1)、求直线的解析式;(2)、若为点上方轴上的一动点,以为直角顶点,为腰在第二象限内作等腰直角 , 连接并延长交轴于点 , 当点运动时,点的位置是否发生变化?如果不变,请求出它的坐标;如果有变化,请说明理由.25. 如图,在中, , , 点P,Q分别是射线 , 射线上的动点,点E在线段上,且 , , 设为x.
(1)、求直线的解析式;(2)、若为点上方轴上的一动点,以为直角顶点,为腰在第二象限内作等腰直角 , 连接并延长交轴于点 , 当点运动时,点的位置是否发生变化?如果不变,请求出它的坐标;如果有变化,请说明理由.25. 如图,在中, , , 点P,Q分别是射线 , 射线上的动点,点E在线段上,且 , , 设为x. (1)、当点Q运动到中点时,恰好 , 求的长度;(2)、在(1)的条件下,在点P和点Q运动过程中,是否存在x的值,使得以A,B,P,Q为顶点的四边形是平行四边形?若存在,求出x的值;若不存在,请说明理由.(3)、连接 , 当点P在运动时,有最小值为 , 求此时的长.
(1)、当点Q运动到中点时,恰好 , 求的长度;(2)、在(1)的条件下,在点P和点Q运动过程中,是否存在x的值,使得以A,B,P,Q为顶点的四边形是平行四边形?若存在,求出x的值;若不存在,请说明理由.(3)、连接 , 当点P在运动时,有最小值为 , 求此时的长.