广东省惠州市惠阳区2022-2023学年八年级下学期期末数学试题

试卷更新日期：2023-08-03 类型：期末考试

进入出卷网下载

一、单选题

1. 下列给出的式子是二次根式的是（）

A、±3 B、 $\sqrt{5}$ C、 $\sqrt{3 - π}$ D、 $\sqrt[3]{a}$

查看试题解析
2. 下列长度的各组线段中，不能构成直角三角形的是（）

A、4、5、6 B、5、12、13 C、3、4、5 D、1、 $\sqrt{2}$ 、 $\sqrt{3}$

查看试题解析
3. 一次函数 $y = x + 1$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算，结果正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $\sqrt{3} \times \sqrt{5} = 15$ C、 $\sqrt{32} \div \sqrt{8} = 2$ D、 $2 \sqrt{3} - \sqrt{3} = 2$

查看试题解析
5. 如图，两个一次函数图象的交点坐标为(2，4)，则关于x，y的方程组 ${\begin{array}{l} k_{1} x + b_{1} - y = 0 \\ k_{2} x + b_{2} - y = 0 \end{array}$ 的解为（　　）

A、 ${\begin{array}{l} x = 2 \\ y = 4 \end{array}$ B、 ${\begin{array}{l} x = 4 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = - 4 \\ y = 0 \end{array}$ D、 ${\begin{array}{l} x = 3 \\ y = 0 \end{array}$

查看试题解析
6. 如图，在四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定四边形ABCD为平行四边形的是（）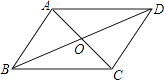

A、AB∥CD，AD∥BC B、OA=OC，OB=OD C、AD=BC，AB∥CD D、AB=CD，AD=BC

查看试题解析
7. 在学校举办的学习强国演讲比赛中，李华根据九位评委所给的分数制作了如下表格：
平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（　　）

A、平均数 B、众数 C、方差 D、中位数

查看试题解析
8. 如图，有一根电线杆垂直立在地面 $D$ 处，在电线杆的点 $C$ 处引拉线固定电线杆，拉线 $A C = B C = 6 m$ ，且和地面成 $60 °$ ，则电线杆引线处 $C$ 离地面的高度（即 $C D$ 的长）是（）

A、 $3 m$ B、 $\sqrt{3} m$ C、 $2 \sqrt{3} m$ D、 $3 \sqrt{3} m$

查看试题解析
9. 在一次演讲比赛中，某位选手的演讲内容、演讲表达的得分分别为95分，90分，将演讲内容、演讲表达的成绩按 $6 ： 4$ 计算，则该选手的成绩是（）

A、94分 B、93分 C、92分 D、91分

查看试题解析
10. 如图，E、F分别是正方形 $A B C D$ 的边 $C D 、 A D$ 上的点，且 $C E = D F$ ， $A E 、 B F$ 相交于点O，下列结论： ① $A E = B F$ ；② $A E ⊥ B F$ ；③ $A O = O E$ ；④ $S_{△ A O B} = S_{四边形 D E O F}$ ，其中正确的有（）

A、①②③ B、②③④ C、①③④ D、①②④

查看试题解析

二、填空题

11. 计算 $\sqrt{{(- 2)}^{2}}$ 的结果是.

查看试题解析
12. 如图，在 $△ A B C$ 中， $A B = 4 ， A C = 5 ， B C = 6$ ，点D，E，F分别是 $A B ， B C ， C A$ 的中点，连结 $D E ， E F$ ，则四边形 $A D E F$ 的周长为．

查看试题解析
13. 如图所示的衣架可以近似看成一个等腰三角形ABC，其中 $A B = A C = 25 c m$ ，底边BC的长 $48 c m$ ，那么衣架的高 $A D =$ $c m$ .

查看试题解析
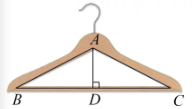14. 对甲、乙两同学100米短跑进行5次测试，他们的成绩通过计算得 $\bar{x_{甲}} = \bar{x_{乙}}$ ， $S_{甲}^{2} = 0.25$ ， $S_{乙}^{2} = 0.016$ ，成绩比较稳定的是．（填“甲”或“乙”）

查看试题解析
15. 如图，甲乙两人以相同的路线前往距离单位 $10 k m$ 的培训中心参加学习，图中 $L_{甲}$ ， $L_{乙}$ 分别表示甲乙两人前往目的地所走的路程S（千米）随时间t（分）变化的函数图象，以下说法：①乙比甲提前 $12$ 分钟到达；②甲、乙相遇时，乙走了6千米；③乙出发6分钟后追上甲．其中正确的是．（填序号）

查看试题解析

三、解答题

16. 已知 $x = 2 + \sqrt{3}$ ， $y = 2 - \sqrt{3}$ ，求下列各式的值：

(1)、 $x^{2} - y^{2}$ ；

(2)、 $x^{2} + x y + y^{2}$ ．

查看试题解析
17. 某城市出租车的收费标准为： $3$ 千米以内（含 $3$ 千米）收费 $8$ 元，超过 $3$ 千米时，超过部分每千米收费 $1.4$ 元．

(1)、写出车费 $y$ （元）和行车里程 $x$ （千米）之间的关系式；

(2)、甲乘坐 $13$ 千米需付多少元钱？

查看试题解析
18. 如图，有一只摆钟，摆锤看作一个点，当摆锤静止时，它离底座的垂直高度 $D E = 4 c m$ ，当摆锤摆动到最高位置时，它离底座的垂直高度 $B F = 6 c m$ ，此时摆锤与静止位置时的水平距离 $B C = 8 c m$ 时，求钟摆 $A D$ 的长度．

查看试题解析
19. 某校学生会向全校2100名学生发起了“爱心捐助”捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如图1、图2所示的统计图．
请根据相关信息，解答下列问题：

(1)、本次接受随机调查的学生人数为，图1中30元所对的圆心角度数是．

(2)、本次调查获取的样本数据的平均数为元、众数为元、中位数为元；

(3)、根据样本数据，估计该校本次活动捐款金额不少于30元的学生人数．

查看试题解析
20. 如图，在 $△ A B C$ 中， $∠ C = 90 ° ， A C = 8 ， B C = 6 ， D E$ 是 $△ A B D$ 的边 $A B$ 上的高，E为垂足且 $A D = 2 \sqrt{5} ， B D = 4 \sqrt{5}$ ．

(1)、试判断 $△ A B D$ 的形状，并说明理由．

(2)、求 $D E$ 的长．

查看试题解析
21. 如图，在平行四边形 $A B C D$ 中， $D E$ 平分 $∠ A D B$ ，交 $A B$ 于点 $E$ ．

(1)、尺规作图：作 $∠ C B D$ 的平分线交 $C D$ 于点 $F$ ．

(2)、在（1）的基础上，求证： $D E = B F$ ．

(3)、在前面2问的基础上，若 $A D = B D$ ，求证：四边形 $D E B F$ 是矩形．

查看试题解析
22. 如图，正方形 $A B C D$ 的边长是 $10$ ．点 $P$ 是正方形 $A B C D$ 对角线 $A C$ 上一动点，过 $P$ 点分别作 $A B$ 、 $B C$ 的垂线，垂足分别为 $E$ ， $F$

(1)、若 $A P = 2 \sqrt{2}$ ，求 $B E$ 的长；

(2)、请你猜想 $E F$ 与 $D P$ 的数量关系，并给出证明；

(3)、在 $P$ 点运动过程中， $E F$ 的长也随之变化，直接写出 $E F$ 的最小值．

查看试题解析
23. 如图，直线 $l_{1}$ 与 $x$ 轴， $y$ 轴分别交于 $A (2 ， 0)$ ， $B$ 两点，点 $P (- 1 ， 3)$ 为直线 $l_{1}$ 上一点，另一直线 $l_{2}$ ： $y = \frac{1}{2} x + b$ 过点 $P$ ，与 $x$ 轴交于点 $C$ ．

(1)、分别求出直线 $l_{1}$ 和 $l_{2}$ 的解析式，并直接写出点 $B$ 和点 $C$ 的坐标；

(2)、若动点 $Q$ 从点 $C$ 开始以每秒 $1$ 个单位的速度向 $x$ 轴正方向移动，设点 $Q$ 的运动时间为 $t$ 秒．
①当点 $Q$ 在运动过程中，请求出 $△ A P Q$ 的面积 $S$ 与 $t$ 的函数关系式；
②求出当 $t$ 为多少时， $△ A P Q$ 的面积等于 $3$ ．

查看试题解析

平均数	中位数	众数	方差
8.5	8.3	8.1	0.15