广东省广州市花都区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-03 类型:期末考试
一、单选题
-
1. 下列根式是最简二次根式的是( )A、 B、 C、 D、2. 校运会100米项目预赛,15名运动员的成绩各不相同,取前8名参加决赛,其中运动员小米已经知道自己的成绩他想确定自己是否进入决赛,只需要知道这15名运动员成绩的( )A、平均数 B、众数 C、中位数 D、方差3. 根据如图所示的数据,的长为( )
 A、2 B、 C、4 D、4. 下列函数中,是一次函数的是( )A、 B、 C、 D、5. 下列二次根式的运算正确的是( )A、 B、 C、 D、6. 如图,平行四边形的对角线相交于点O,且 , 则的周长为( )
A、2 B、 C、4 D、4. 下列函数中,是一次函数的是( )A、 B、 C、 D、5. 下列二次根式的运算正确的是( )A、 B、 C、 D、6. 如图,平行四边形的对角线相交于点O,且 , 则的周长为( ) A、27 B、28 C、29 D、307. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?“这道题讲的是:有一块三角形沙田,三条边长分别为里,里,里,则该沙田的面积为( )平方里.A、 B、 C、 D、8. 对于一次函数 , 下列结论正确的是( )A、函数值随自变量的增大而增大 B、函数的图象经过第三象限 C、函数的图象与轴的交点坐标是 D、函数的图象向下平移4个单位得的图像9. 如图,在平面直角坐标系中,四边形是矩形,点的坐标为 , 点的坐标为 , 点分别是各边的中点,顺次连接各中点,并连接交于点 , 点为的中点,则的长为( )
A、27 B、28 C、29 D、307. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?“这道题讲的是:有一块三角形沙田,三条边长分别为里,里,里,则该沙田的面积为( )平方里.A、 B、 C、 D、8. 对于一次函数 , 下列结论正确的是( )A、函数值随自变量的增大而增大 B、函数的图象经过第三象限 C、函数的图象与轴的交点坐标是 D、函数的图象向下平移4个单位得的图像9. 如图,在平面直角坐标系中,四边形是矩形,点的坐标为 , 点的坐标为 , 点分别是各边的中点,顺次连接各中点,并连接交于点 , 点为的中点,则的长为( ) A、2 B、2.5 C、1.5 D、310. 如图,在边长为10的正方形对角线上有E,F两个动点,且 , 点P是中点,连接 , 则最小值为( )
A、2 B、2.5 C、1.5 D、310. 如图,在边长为10的正方形对角线上有E,F两个动点,且 , 点P是中点,连接 , 则最小值为( ) A、 B、 C、 D、10
A、 B、 C、 D、10二、填空题
-
11. 要使式子有意义,则x的取值范围12. 甲、乙两人参加月日世界卫生日“健康知识”竞赛,经过轮比赛,他们的平均成绩都是分.若两人比赛成绩的方差分别为 , , 则两人中比赛成绩更加稳定的是 .13. 已知一次函数的图象经过点、 , 则(填“”、“”或“”).14. 如图,四边形是菱形,对角线与相交于点O,请添加条件 , 使得菱形为正方形.(只能添加一个条件)
 15. 点、是一次函数图象上的两个点,则 .16. 如图,正方形的边长为4,E是上一点,且 , 过点E作交点P,过点P作于点G,连接 , 下列结论:①;②;③;④正确的是: .
15. 点、是一次函数图象上的两个点,则 .16. 如图,正方形的边长为4,E是上一点,且 , 过点E作交点P,过点P作于点G,连接 , 下列结论:①;②;③;④正确的是: .
三、解答题
-
17. 计算:18. 计算: .19. 如图,矩形的对角线交于点 , 过点作 , 过点作与相交于点 , 试判断四边形的形状,并说明理由.

解:四边形的形状是 ▲ , 理由如下:
∵ ▲
∴四边形是平行四边形
∵四边形是矩形
∴ ▲ (矩形对角线相等) ▲ (矩形对角线互相平分)
∴(等量代换)
∵在平行四边形中
∴四边形的形状是 ▲ .
20. 2023年广州市体育中考保持分值不变,满分为70分,由统一考试50分和体育素质综合评价20分构成.其中统一考试模式由“必考(二选一)+选考一(五选一)+选考二(三选一)”调整为“十选二”,给予学生充分多样的选择,并减少一项考试项目.某校从九年级选考“一分钟跳绳”330名同学中随机抽得12名同学的跳绳个数(单位:个)如下:181,210,196,173,182,198,182,195,182,212,213,197.(1)、样本数据(12名同学的一分钟跳绳个数)的中位数是 , 众数是 .(2)、已知中考体育一分钟跳绳达到182个即为满分,试估计该校九年级选考一分钟跳绳的330名学生中有多少人能取得满分?21. 如图,在中, , , 边上的中线 , 延长至点 , 使 , 连接 .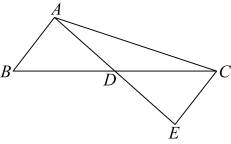 (1)、求证: .(2)、求的长.22. 如图在平行四边形中, , 将边延长到点 , 使 , 连接交于点 , 连接 .
(1)、求证: .(2)、求的长.22. 如图在平行四边形中, , 将边延长到点 , 使 , 连接交于点 , 连接 . (1)、求证:四边形是平行四边形;(2)、若 , 求四边形周长.23. 为了贯彻双减要求,丰富校园文化生活,增强班级团队凝聚力,某校八年级今年计划举办一场主题为“缤纷六月,篮出梦想”的首届“校”班际篮球赛.该校计划为班际篮球赛购置若干个篮球,经过与某体育用品店经销商沟通,型号篮球的单价比型号的篮球单价多40元,且用1200元购买型号篮球个数与用600元购买型号篮球的个数相等.(1)、求型号篮球和型号篮球的单价分别是多少元?(2)、该体育用品店给出了两种让利活动,购买时只能选择其中一种方案.
(1)、求证:四边形是平行四边形;(2)、若 , 求四边形周长.23. 为了贯彻双减要求,丰富校园文化生活,增强班级团队凝聚力,某校八年级今年计划举办一场主题为“缤纷六月,篮出梦想”的首届“校”班际篮球赛.该校计划为班际篮球赛购置若干个篮球,经过与某体育用品店经销商沟通,型号篮球的单价比型号的篮球单价多40元,且用1200元购买型号篮球个数与用600元购买型号篮球的个数相等.(1)、求型号篮球和型号篮球的单价分别是多少元?(2)、该体育用品店给出了两种让利活动,购买时只能选择其中一种方案.方案一:所有商品打9折销售
方案二:买3个型号篮球,免费赠送1个型号篮球(不足3个不赠送).
若该校需要购买15个型号篮球和()个型号篮球,则上述两种购买方案中,哪一种方案更省钱,并说明理由.
24. 如图,在梯形 中, , , , , , 动点从点开始沿边向以1cm/秒的速度运动,动点从点开始沿边向以3cm/秒的速度运动,分别从同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为秒.问: (1)、的长度为 , 的长度为 , (用的式子表示),其中的取值范围为 .(2)、当为何值时,四边形是平行四边形,请说明理由;(3)、朱华同学研究发现:按以上变化,四边形在变化过程中不可能为菱形,除非改变动点的运动速度.请探究如何改变点的速度(匀速运动),使四边形在某一时刻为菱形,求此时点的速度.25. 定义:如图,只有一组对角是直角的四边形叫做“损矩形”.
(1)、的长度为 , 的长度为 , (用的式子表示),其中的取值范围为 .(2)、当为何值时,四边形是平行四边形,请说明理由;(3)、朱华同学研究发现:按以上变化,四边形在变化过程中不可能为菱形,除非改变动点的运动速度.请探究如何改变点的速度(匀速运动),使四边形在某一时刻为菱形,求此时点的速度.25. 定义:如图,只有一组对角是直角的四边形叫做“损矩形”. (1)、如图1,点P在直线上且横坐标是4,点 , 点 , 连接 . 判断:四边形损矩形(填“是”或“不是”);(2)、如图2,点E在y轴正半轴上,点F在x轴正半轴上,点P是直线上位于第一象限的一个动点,四边形是“损矩形”,请确定:与的数量关系,并说明理由;(3)、如图3,若 ,
(1)、如图1,点P在直线上且横坐标是4,点 , 点 , 连接 . 判断:四边形损矩形(填“是”或“不是”);(2)、如图2,点E在y轴正半轴上,点F在x轴正半轴上,点P是直线上位于第一象限的一个动点,四边形是“损矩形”,请确定:与的数量关系,并说明理由;(3)、如图3,若 ,①在直线:上找一个点Q,使得四边形为损矩形,求点Q的坐标;
②K点也在直线:上且 , 直接写出K坐标.