广东省广州市黄埔区2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-08-03 类型:期末考试
一、单选题
-
1. 下列各数是无理数的是( )A、 B、 C、 D、2. 已知 , 下列不等式变形中正确的是( )A、 B、 C、 D、3. 如图,∠1和∠2不是同位角的是( )A、
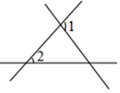 B、
B、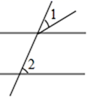 C、
C、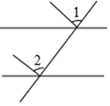 D、
D、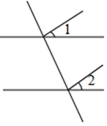 4. 下列各方程是二元一次方程的是( )A、 B、 C、 D、5. 下面调查方式中,合适的是( )A、调查你所在班级同学的身高,采用抽样调查方式 B、调查长江的水质情况,采用抽样调查的方式 C、调查某栏目的收视率,采用全面调查的方式 D、要了解全市初中学生的业余爱好,采用全面调查的方式6. 已知点 在第二象限且到 轴的距离为3,到 轴的距离为2,则 点坐标为( )A、 B、 C、 D、7. 方程组的解为 , 则被遮盖的两个数、分别是( )A、2,1 B、2,3 C、5,1 D、5,48. 下列计算中正确的是( )A、 B、 C、 D、9. 如图, , 平分 , 平分 , , 则下列结论:①;②;③;④;⑤ . 其中正确结论有( )
4. 下列各方程是二元一次方程的是( )A、 B、 C、 D、5. 下面调查方式中,合适的是( )A、调查你所在班级同学的身高,采用抽样调查方式 B、调查长江的水质情况,采用抽样调查的方式 C、调查某栏目的收视率,采用全面调查的方式 D、要了解全市初中学生的业余爱好,采用全面调查的方式6. 已知点 在第二象限且到 轴的距离为3,到 轴的距离为2,则 点坐标为( )A、 B、 C、 D、7. 方程组的解为 , 则被遮盖的两个数、分别是( )A、2,1 B、2,3 C、5,1 D、5,48. 下列计算中正确的是( )A、 B、 C、 D、9. 如图, , 平分 , 平分 , , 则下列结论:①;②;③;④;⑤ . 其中正确结论有( ) A、5个 B、4个 C、3个 D、2个10. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点 , 第二次从点运动到点 , 第三次从点运动到点 , …,按这样的运动规律,第2023次从点运动到点后,此时点的坐标是( )
A、5个 B、4个 C、3个 D、2个10. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点 , 第二次从点运动到点 , 第三次从点运动到点 , …,按这样的运动规律,第2023次从点运动到点后,此时点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 121的平方根是 .12. 如图,若 , , 则度.
 13. 如图为某天参观文化馆的学生人数统计图,则图中代表小学生的扇形圆心角度数是度.
13. 如图为某天参观文化馆的学生人数统计图,则图中代表小学生的扇形圆心角度数是度. 14. 已知关于x,y的二元一次方程组 , 则 .15. 若不等式可以变形为 , 则a的取值范围是 .16. 表示不大于a的最大整数,例如 , 那么方程的解是 .
14. 已知关于x,y的二元一次方程组 , 则 .15. 若不等式可以变形为 , 则a的取值范围是 .16. 表示不大于a的最大整数,例如 , 那么方程的解是 .三、解答题
-
17. 解方程组:18. 计算: .19. 已知三个顶点的坐标是 , 将先向右平移3个单位长度,再向下平移2个单位长度,得到 .
 (1)、请画出平移后的图形;(2)、请直接写出点的坐标.20. 某校为调查七年级学生一分钟踢毽子的水平,在七年级随机抽取了若干名学生并统计他们一分钟踢毽子的次数,调查结果记录如下(单位:次):
(1)、请画出平移后的图形;(2)、请直接写出点的坐标.20. 某校为调查七年级学生一分钟踢毽子的水平,在七年级随机抽取了若干名学生并统计他们一分钟踢毽子的次数,调查结果记录如下(单位:次):45 20 23 52 38 37 36 39 11 45
49 41 88 42 43 46 50 52 53 53
58 70 57 57 22 60 67 68 68 61
69 69 57 71 76 79 42 87 83 91
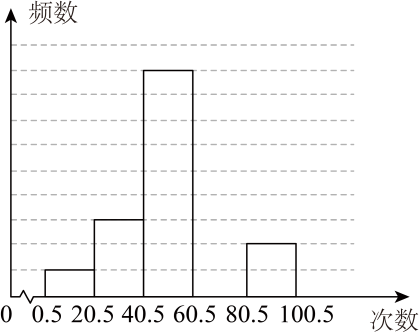 (1)、下图是根据上述数据绘制的不完整的频数分布直方图,请补全直方图;(2)、若规定一分钟踢毽子60次以上(不含60次)为优秀,该校七年级总人数为320人,请你估计该年级有多少学生一分钟踢毽子的次数达到优秀水平.21. 请把下面的证明过程补充完整:
(1)、下图是根据上述数据绘制的不完整的频数分布直方图,请补全直方图;(2)、若规定一分钟踢毽子60次以上(不含60次)为优秀,该校七年级总人数为320人,请你估计该年级有多少学生一分钟踢毽子的次数达到优秀水平.21. 请把下面的证明过程补充完整:已知:如图和相交于点E, , , , .求证: .
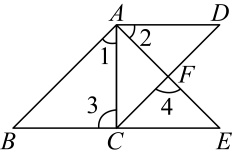
证明:∵(已知)
∴ ▲ ( ).
∵(已知)
∴ ▲ ( )
∵已知)
∴( )
即 ▲ .
∴ ▲ (等量代换)
∴( ).
22. 某商店销售一批跑步机,第一个月以5000元/台的价格售出20台,第二个月起降价,以4500元/台的价格将这批跑步机全部售出销售总额超过35万元.这批跑步机最少有多少台?23. 如图,在直角坐标系中,将线段平移至 , 已知 , 连接 , 点D在射线上移动(不与点O、A重合).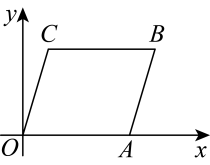 (1)、直接写出点C的坐标;(2)、点D在运动过程中,是否存在的面积等于324. 快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需7万元;购买甲型机器人2台,乙型机器人3台,共需12万元.(1)、甲,乙两种型号机器人的单价各为多少万元?(2)、已知1台甲型和1台乙型机器人每小时分拣快递的数量分别是1400件和1200件,该公司计划最多用16万元购买6台这两种型号的机器人,且至少购买甲型机器人2台,如何购买才能使每小时的分拣量最大?25. 已知直线与直线分别交于E、F两点,和的角平分线交于点P,且 .
(1)、直接写出点C的坐标;(2)、点D在运动过程中,是否存在的面积等于324. 快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需7万元;购买甲型机器人2台,乙型机器人3台,共需12万元.(1)、甲,乙两种型号机器人的单价各为多少万元?(2)、已知1台甲型和1台乙型机器人每小时分拣快递的数量分别是1400件和1200件,该公司计划最多用16万元购买6台这两种型号的机器人,且至少购买甲型机器人2台,如何购买才能使每小时的分拣量最大?25. 已知直线与直线分别交于E、F两点,和的角平分线交于点P,且 . (1)、求证:;(2)、如图2,和的角平分线交于点Q,求的度数;(3)、如图3,若 , 延长线段得射线 , 延长线段得射线 , 射线绕点E以每秒的速度逆时针旋转后停止,射线绕点F以每秒的速度顺时针旋转以后停止.设它们同时开始旋转,当射线时,求满足条件的t的值为多少.
(1)、求证:;(2)、如图2,和的角平分线交于点Q,求的度数;(3)、如图3,若 , 延长线段得射线 , 延长线段得射线 , 射线绕点E以每秒的速度逆时针旋转后停止,射线绕点F以每秒的速度顺时针旋转以后停止.设它们同时开始旋转,当射线时,求满足条件的t的值为多少.