广东省广州市从化区2022-2023学年七年级下册数学期末试卷
试卷更新日期:2023-08-03 类型:期末考试
一、单选题
-
1. 以下所示的车标,可以看作由平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列属于无理数的是( )A、 B、 C、 D、53. 为了解某校名学生每天的阅读时间,从中抽取名学生进行调查,其中的是( )A、总体 B、个体 C、样本 D、样本容量4. 下列命题属于真命题的是( )A、同旁内角相等,两直线平行 B、相等的角是对顶角 C、平行于同一条直线的两条直线平行 D、同位角相等5. 下列说法正确的是( )A、1的平方根是1 B、的立方根是1 C、0的平方根是0 D、0.01是0.1的一个平方根6. 如图所示的是超市里购物车的侧面示意图,扶手与车底平行, , , 则的度数是( )
2. 下列属于无理数的是( )A、 B、 C、 D、53. 为了解某校名学生每天的阅读时间,从中抽取名学生进行调查,其中的是( )A、总体 B、个体 C、样本 D、样本容量4. 下列命题属于真命题的是( )A、同旁内角相等,两直线平行 B、相等的角是对顶角 C、平行于同一条直线的两条直线平行 D、同位角相等5. 下列说法正确的是( )A、1的平方根是1 B、的立方根是1 C、0的平方根是0 D、0.01是0.1的一个平方根6. 如图所示的是超市里购物车的侧面示意图,扶手与车底平行, , , 则的度数是( ) A、 B、 C、 D、7. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、8. (我国古代问题)有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛,古代一种容量单位),1个大桶加上5个小桶可以盛酒2斛.若设1一个大桶可以盛酒斛,1个小桶可以盛酒斛,则列方程组为( )A、 B、 C、 D、9. 将一副三角板的直角顶点重合按如图所示方式放置, , , 得到下列结论,其中不正确的结论是( )
A、 B、 C、 D、7. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、8. (我国古代问题)有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛,古代一种容量单位),1个大桶加上5个小桶可以盛酒2斛.若设1一个大桶可以盛酒斛,1个小桶可以盛酒斛,则列方程组为( )A、 B、 C、 D、9. 将一副三角板的直角顶点重合按如图所示方式放置, , , 得到下列结论,其中不正确的结论是( ) A、 B、若 , 则 C、 D、若 , 则10. 已知 , 且 , 则k的取值范围是( )A、 B、 C、 D、
A、 B、若 , 则 C、 D、若 , 则10. 已知 , 且 , 则k的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 在平面直角坐标系中,点到y轴的距离是 .12. 若是方程的解,则a的值为 .13. 比较大小:3(用“>”或“<”连接).14. 如图,将向右平移得到 , 若 , 则 .
 15. 在画从化区某校某班身高频数分布直方图时,一组数据的最小值为 , 最大值为 , 若确定组距为5,则分成的组数是 .16. 如图,在平面直角坐标系中有一个点 , 点第一次向左跳动至 , 第二次向右跳动至 , 第三次向左跳动至 , 第四次向右跳动至 , …,依照此规律跳动下去,点第2023次跳动到点的坐标为
15. 在画从化区某校某班身高频数分布直方图时,一组数据的最小值为 , 最大值为 , 若确定组距为5,则分成的组数是 .16. 如图,在平面直角坐标系中有一个点 , 点第一次向左跳动至 , 第二次向右跳动至 , 第三次向左跳动至 , 第四次向右跳动至 , …,依照此规律跳动下去,点第2023次跳动到点的坐标为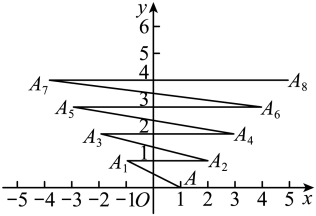
三、解答题
-
17. 计算: .18. 解方程组19. 解不等式组 , 把解集在数轴上表示出来.
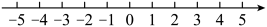 20. 如图,直线、相交于点O, , 若 , , 求度数.
20. 如图,直线、相交于点O, , 若 , , 求度数. 21. 如图,在平面直角坐标系中,点A、B、C的坐标分别为、、 , 将先向右平移4个单位,再向下平移3个单位得到 .
21. 如图,在平面直角坐标系中,点A、B、C的坐标分别为、、 , 将先向右平移4个单位,再向下平移3个单位得到 . (1)、请在图中画出;(2)、写出平移后的三个顶点的坐标;
(1)、请在图中画出;(2)、写出平移后的三个顶点的坐标;( , )
( , )
( , )
(3)、求的面积.22. 某校为进一步落实“双减”政策,通过对本校学生进行调查了解学生的体育兴趣,组建更多符合学生爱好需求的体育社团,根据调查结果,最受学生喜爱的体育项目有:篮球、足球、羽毛球、乒乓球和其他共五类,根据调查的部分数据,绘制的统计图如下: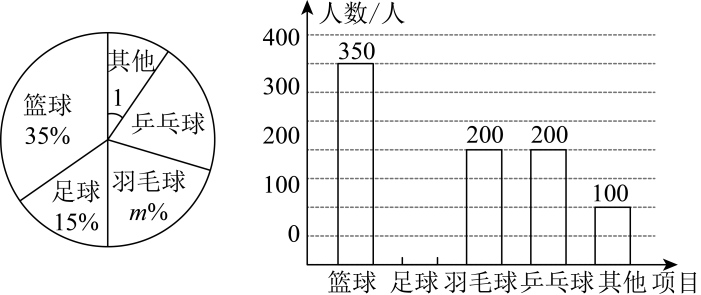
根据所给的信息解答下列问题:
(1)、一共调查了学生人;(2)、 , ;(3)、请补全条形统计图并在图中标明相应数据;(4)、若全校约有3000名学生,请估计喜欢羽毛球的人数约为多少人.23. 如图, , 平分 , 平分 , . (1)、证明:;(2)、请判断与是否平行?请说明理由.24. 某电器超市销售进价分别为200元/台,170元/台的A、B两种型号的电风扇.下表是近两周的销售情况:
(1)、证明:;(2)、请判断与是否平行?请说明理由.24. 某电器超市销售进价分别为200元/台,170元/台的A、B两种型号的电风扇.下表是近两周的销售情况:销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
1800元
第二周
4台
10台
3100元
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)、求A、B两种型号的电风扇的销售单价;(2)、如果购买A、B两种型号的电风扇共30台,且购买A种型号的数量不高于B种型号数量的3倍,求最多可购买多少台A种型号的电风扇?(3)、在(2)的前提下,要求销售完这批电风扇实现利润不低于1410元,请问有哪几种购买方案?哪种方案利润最高?25. 在平面直角坐标系中,已知点、、 , 且满足 , 线段交y轴于点F,点D是y轴正半轴上的一点. (1)、求出点A、B的坐标;(2)、如图1,若 , , 且、别平分 , , 求的度数(用含的代数式表示);(3)、如图2,坐标轴上是否存在一点P,使得面积和面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
(1)、求出点A、B的坐标;(2)、如图1,若 , , 且、别平分 , , 求的度数(用含的代数式表示);(3)、如图2,坐标轴上是否存在一点P,使得面积和面积相等?若存在,求出P点的坐标;若不存在,请说明理由.