广东省惠州市惠东县2022-2023学七年级下册数学期末试卷
试卷更新日期:2023-08-03 类型:期末考试
一、单选题
-
1. 2的算术平方根是( )A、2 B、4 C、 D、2. 点在平面直角坐标系中所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 在实数 , , , , , 中,无理数有( )A、1个 B、2个 C、3个 D、4个4. 下列说法正确的是( )A、在同一平面内,有且只有一条直线与已知直线垂直. B、同位角一定相等. C、若 , 则 D、了解惠东县西枝江水质情况,适宜采用抽样调查.5. 如图,直线公路l上共有A、B、C、D四个核酸检测点,若从点M用相同速度到任意一个核酸检测点,用时最短的路径是( )
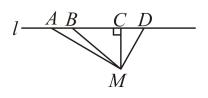 A、 B、 C、 D、6. 如图,直线l1∥l2 , 直线l3与l1 , l2分别交于A,B两点,若∠1=65°,则∠2=( )
A、 B、 C、 D、6. 如图,直线l1∥l2 , 直线l3与l1 , l2分别交于A,B两点,若∠1=65°,则∠2=( )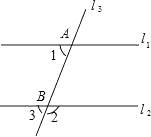 A、65° B、75° C、115° D、125°7. 二元一次方程组的解是( )A、 B、 C、 D、8. 不等式的解集在以下数轴表示中正确的是( )A、
A、65° B、75° C、115° D、125°7. 二元一次方程组的解是( )A、 B、 C、 D、8. 不等式的解集在以下数轴表示中正确的是( )A、 B、
B、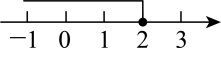 C、
C、 D、
D、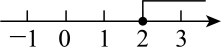 9. 我国古代数学名著《孙子算经》中记载了一道题,大意是:求100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为( )A、 B、 C、 D、10. 下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有4个小圆圈,第②个图形中一共有10个小圆圈,第③个图形中一共有19个小圆圈,…,按此规律排列,则第⑧个图形中小圆圈的个数为( )
9. 我国古代数学名著《孙子算经》中记载了一道题,大意是:求100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为( )A、 B、 C、 D、10. 下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有4个小圆圈,第②个图形中一共有10个小圆圈,第③个图形中一共有19个小圆圈,…,按此规律排列,则第⑧个图形中小圆圈的个数为( ) A、85 B、96 C、100 D、109
A、85 B、96 C、100 D、109二、填空题
-
11. 关于x的不等式的正整数解是 .12. 已知点P坐标为 , 则P点到y轴的距离是 .13. 若是关于x,y的二元一次方程,则 .14. 将点先向右平移2个单位长度后,再向下平移1个单位长度得到点B,则点B的坐标为 .15. 对于实数x,y,定义一种运算“*”如下, , 已知 , , 那么 .
三、解答题
-
16. 计算:17. 如图,已知 , , , . 求的度数.
 18. 解不等式组: ,并将解集在数轴上表示出来.19. 2022年6月5日10时44分,搭载神舟十四号载人飞船的火箭在酒泉卫星发射中心发射成功.为了解学生对我国航天科技及空间站的知晓情况,某校团委在七年级开展了“航天梦科普知识”竞赛活动,并随机抽取了部分同学的成绩(满分为100分,得分均为整数),整理绘制成如图所示的两幅不完整的统计图表.
18. 解不等式组: ,并将解集在数轴上表示出来.19. 2022年6月5日10时44分,搭载神舟十四号载人飞船的火箭在酒泉卫星发射中心发射成功.为了解学生对我国航天科技及空间站的知晓情况,某校团委在七年级开展了“航天梦科普知识”竞赛活动,并随机抽取了部分同学的成绩(满分为100分,得分均为整数),整理绘制成如图所示的两幅不完整的统计图表.成绩x(分)
频数(人)
频率
6
9
27
a
b
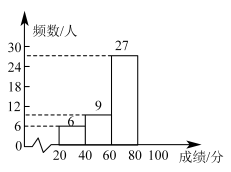
根据以上信息解答下列问题:
(1)、本次调查的样本容量为;(2)、a= ▲ , b= ▲ , 并补全频数分布直方图;(3)、若该校七年级共有720人,估计有多少学生的测试成绩不低于80分?20. 在平面直角坐标系中,三角形ABC的三个顶点的位置如图所示,点A′坐标是(-2,2),现将三角形ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点. (1)、请画出平移后的三角形A′B′C′(不写画法),并写出点B′、C′的坐标;(2)、求三角形ABC的面积.21. 某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)、求每台A型电脑和B型电脑的销售利润:(2)、商场计划在暑假期间,对A型电脑按成本价提高20%后标价,又以9折(即按标价的90%)优惠卖出,结果每台电脑仍可获利90元,则每台A型电脑的成本是多少元?22. 已知方程组的解为非正数,为负数.(1)、求的取值范围:(2)、化简;(3)、在的取值范围内,当取何整数时,不等式的解为?23. 如图,在以点O为原点的平面直角坐标系中点A , B的坐标分别为(a , 0),(a , b),点C在y轴上,且BC x轴,a , b满足 .点P从原点出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线运动(回到O为止).
(1)、请画出平移后的三角形A′B′C′(不写画法),并写出点B′、C′的坐标;(2)、求三角形ABC的面积.21. 某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)、求每台A型电脑和B型电脑的销售利润:(2)、商场计划在暑假期间,对A型电脑按成本价提高20%后标价,又以9折(即按标价的90%)优惠卖出,结果每台电脑仍可获利90元,则每台A型电脑的成本是多少元?22. 已知方程组的解为非正数,为负数.(1)、求的取值范围:(2)、化简;(3)、在的取值范围内,当取何整数时,不等式的解为?23. 如图,在以点O为原点的平面直角坐标系中点A , B的坐标分别为(a , 0),(a , b),点C在y轴上,且BC x轴,a , b满足 .点P从原点出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线运动(回到O为止).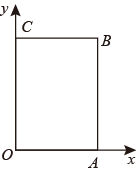 (1)、直接写出点A , B , C的坐标;(2)、当点P运动3秒时,连接PC , PO , 求出点P的坐标,并直接写出∠CPO , ∠BCP , ∠AOP之间满足的数量关系;(3)、点P运动t秒后(t≠0),是否存在点P到x轴的距离为 t个单位长度的情况.若存在,求出点P的坐标;若不存在,请说明理由.
(1)、直接写出点A , B , C的坐标;(2)、当点P运动3秒时,连接PC , PO , 求出点P的坐标,并直接写出∠CPO , ∠BCP , ∠AOP之间满足的数量关系;(3)、点P运动t秒后(t≠0),是否存在点P到x轴的距离为 t个单位长度的情况.若存在,求出点P的坐标;若不存在,请说明理由.