广东省广州市增城区2022-2023学年七年级下册数学期末试卷

试卷更新日期：2023-08-03 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，国家节水标志由水滴，手掌和地球变形而成．以下可以通过平移节水标志得到的图形是（）

A、 B、 C、 D、

查看试题解析
2. 9的算术平方根是（）

A、81 B、 $\pm 9$ C、 $\pm 3$ D、3

查看试题解析
3. 下列四个选项中，为无理数的是（）

A、 $0$ B、 $\sqrt{3}$ C、 $- 1$ D、 $3.14$

查看试题解析
4. 下列调查中，最适合采用全面调查的是（）

A、调查全广州市中学生的睡眠时间 B、调查增江河的水质情况 C、调查某批次汽车的抗撞击能力 D、调查全班同学的视力情况

查看试题解析
5. 下列命题为假命题的是（）

A、垂线段最短 B、同旁内角互补 C、对顶角相等 D、两直线平行，同位角相等

查看试题解析
6. 在平面直角坐标系中，在第二象限内的点是（）

A、 $(1 ， 2)$ B、 $(- 2 ， - 1)$ C、 $(- 2 ， 1)$ D、 $(2 ， - 1)$

查看试题解析
7. 不等式组 ${\begin{array}{l} x + 2 \leq 0 \\ 1 - 2 x > - 1 \end{array}$ 的解集在以下数轴表示中，正确的是（）

A、 B、 C、 D、

查看试题解析
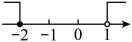8. 如图，下列条件中能判定 $A E ∥ C D$ 是（）

A、 $∠ C = ∠ D B A$ B、 $∠ A + ∠ A B C = 180 °$ C、 $∠ A D B = ∠ D B C$ D、 $∠ C D B = ∠ D B A$

查看试题解析
9. 如图，一副三角尺按如图所示的方式放置，若 $A B ∥ C D$ ，则 $∠ α$ 的度数为（）．

A、 $75 °$ B、 $90 °$ C、 $105 °$ D、 $120 °$

查看试题解析
10. 如图，长方形 $A B C D$ 中放置9个形状、大小都相同的小长方形， $A D$ 与 $A B$ 的差为2，小长方形的周长为14，则图中阴影部分的面积为（）

A、26 B、25 C、24 D、23

查看试题解析

二、填空题

11. 计算： $\sqrt[3]{8}$ = ．

查看试题解析
12. 某学校在“你最喜爱的课外活动项目”调查中，随机调查了若干名学生，并根据调查结果绘制了如图所示的扇形统计图，则“机器人”部分扇形所对的圆心角为度．

查看试题解析
13. 如图， $A B ∥ C D$ ， $∠ A = 24 °$ ， $∠ C = 55 °$ ，则 $∠ E =$ $°$ ．

查看试题解析
14. 已知点 $A$ 坐标为 $(m + 2 ， 2 m)$ ，且点 $A$ 在 $y$ 轴上，则 $m =$ ．

查看试题解析
15. 已知二元一次方程组 ${\begin{array}{l} 3 x - 2 y = 3 \\ x + y = 1 \end{array}$ ，则 $4 x - y$ 的值为．

查看试题解析
16. 如图，已知 $B C ∥ A D$ ， $∠ C = ∠ D A B = 120 °$ ，点E、F在线段 $B C$ 上，且满足 $D B$ 平分 $∠ A D F$ ， $D E$ 平分 $∠ C D F$ ， $A B$ 可以左右平行移动．给出下列四个结论．其中正确的结论有（填写所有正确结论的序号）．
① $A B ∥ C D$ ；
② $∠ D E C + ∠ D B A = 90 °$ ；
③ $∠ D E C = 2 ∠ D B F$ ；
④ $\frac{∠ A D C + ∠ C D F}{∠ A B D} = 2$

查看试题解析

三、解答题

17. 计算： $\sqrt[3]{- 27} - \sqrt{4} + \sqrt{{(- 2)}^{2}}$ ．

查看试题解析
18. 解方程组： ${\begin{array}{l} 2 x + 3 y = 3 \\ x - 3 y = 6 \end{array}$

查看试题解析
19. 解不等式组： ${\begin{array}{l} x - 1 < 2 \\ 3 (x + 1) \geq 2 x + 2 \end{array}$ ，并把它的解集在数轴上表示出来．

查看试题解析

20. 学校为了解学生每周体育锻炼时间，在本校随机抽取了若干名学生进行调查，并依据调查结果绘制了以下两幅不完整的统计图，请根据图中的信息，解答下列问题：

频数分布表

时间（小时）	频数（人数）	频率
$2 \leq x < 3$	4	0.1
$3 \leq x < 4$	10	0.25
$4 \leq x < 5$	a	0.15
$5 \leq x < 6$	8	b
$6 \leq x < 7$	12	0.3
合计		1

(1)、频数分布表中的

a =

，

b =

；

(2)、请补全频数分布直方图；

(3)、若该校共有1600名学生，试估计全校每周参加体育锻炼时间不低于4小时的学生约为多少名？

查看试题解析

21. 如图，已知 $△ A B C$ 在平面直角坐标系中，将 $△ A B C$ 向右平移6个单位长度，再向下平移4个单位长度，得到 $△ A_{1} B_{1} C_{1}$ （图中每个小方格边长均为1个单位长度）．

(1)、在图中画出 $△ A_{1} B_{1} C_{1}$ ；

(2)、直接写出 $△ A_{1} B_{1} C_{1}$ 三个顶点的坐标；

(3)、求 $△ A_{1} B_{1} C_{1}$ 的面积．

查看试题解析
22. 如图，点D、E在 $A B$ 上，点F、G分别在 $B C$ 、 $A C$ 上，且 $D G ∥ B C$ ， $∠ 1 = ∠ 2$ ．

(1)、求证： $D C ∥ E F$ ；

(2)、若 $E F ⊥ A B$ ， $∠ 1 = 55 °$ ，求 $∠ A D G$ 的度数．

查看试题解析
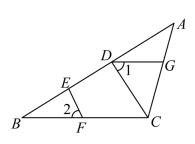23. 某市为了提高市民的交通安全意识，要求骑行过程中必须佩戴安全头盔，可以保护头部，减少伤害．某商店经销甲、乙两种安全头盔，进价、售价见下表．

甲

乙

进价（元/顶）

40

30

售价（元/顶）

60

m

(1)、若该商店进货甲、乙两种安全头盔共100顶，一共花费了3700元，求甲、乙两种安全头盔分别进货多少顶？

(2)、在（1）的条件下，将头盔全部售出，商家把乙种安全头盔的售价m至少定为多少元，才能保证利润不低于1700元？

查看试题解析
24. 如图，点 $A (a ， 0)$ 和 $B (b ， 0)$ 满足 ${(a + 2)}^{2} + | b - 4 | = 0$ ，现同时将点A，B分别向上平移4个单位长度，得向右平移2个单位长度，得到点A，B的对应点分别为点C，D，连接 $A C ， B D ， C D ．$

(1)、求点A，B的坐标；

(2)、在x轴上是否存在点P，使 $△ P A C$ 面积等于四边形 $O B D C$ 的面积？若存在，求出点P的坐标；若不存在，请说明理由．

(3)、点Q从点O出发，以每秒1个单位长度的速度向点B匀速运动，过点Q作 $C D$ 的垂线，交 $C D$ 于点M，当点Q到达点B时，整个运动过程随之结束．设运动时间为t秒，是否存在t，使得 $Q M$ 将四边形 $O B D C$ 的面积分成 $2 ： 3$ 两部分？若存在，求t的值；若不存在，请说明理由．

查看试题解析
25. 如图1，已知两条直线 $A B ， C D$ 被直线 $E F$ 所截，分别交于点 $E ， F ， E M$ 平分 $∠ A E F$ 交 $C D$ 于点 $M$ ，且 $∠ F E M = ∠ F M E$ ．

(1)、求证： $A B ∥ C D$ ；

(2)、点 $G$ 是射线 $M D$ 上一动点（不与点 $M ， F$ 重合），连接 $E G ， E H$ 平分 $∠ F E G$ 交 $C D$ 于点 $H$ ，过点 $H$ 作 $H N ⊥ E M$ 于点 $N$ ， $∠ E H N = α$ ， $∠ E G F = β$ ．
①如图2，当点G在点F的右侧时，若 $β = 60 °$ ，求 $α$ 的度数；
②点G在运动过程中，探究 $α$ 和 $β$ 两者之间的数量关系，并说明理由．

查看试题解析

	甲	乙
进价（元/顶）	40	30
售价（元/顶）	60	m