贵州省黔西南州2022-2023学年高一下学期期末教学质量检测数学试题

试卷更新日期：2023-08-03 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {- 1 ， 0 ， 1}$ ，集合 $B = {0 ， 1 ， 2}$ ，则 $A ∩ B =$ （）

A、 ${0 ， 1}$ B、 ${- 1 ， 0 ， 1}$ C、 ${0 ， 1 ， 2}$ D、 ${- 1 ， 0 ， 1 ， 2}$

查看试题解析
2. 若 $z + 2 - 3 i = 3 - 2 i$ （ $i$ 为虚数单位），则 $z =$ （）

A、 $5 - 5 i$ B、 $1 + i$ C、 $1 + 5 i$ D、 $\frac{a_{n}}{a_{n - 1}} = 2 (n \geq 2 ， n \in N^{*})$

查看试题解析
3. 已知向量 $\vec{a} = (- 2 ， 3)$ ， $\vec{b} = (4 ， - 2)$ ，则 $\vec{a} + \vec{b} =$ （）

A、 $(- 2 ， 1)$ B、 $(- 2 ， - 1)$ C、 $(2 ， 1)$ D、 $(- 2 ， 5)$

查看试题解析
4. 将一组从小到大排列的数据如下：50，51，52，53，54，55，56，57，58，59，这组数据的第60百分位数是（）

A、55 B、55.5 C、56 D、56.5

查看试题解析
5. 下列函数中，在定义域上单调递增的是（）

A、 $f (x) = \frac{1}{x}$ B、 $f (x) = {(\frac{1}{2})}^{x}$ C、 $f (x) = - 2 x + 1$ D、 $f (x) = l o g_{2} x$

查看试题解析
6. 函数 $y = x + \frac{4}{x} - 1$ 在 $(0 ， + ∞)$ 上的最小值是（）

A、 $- 2$ B、1 C、2 D、3

查看试题解析
7. 端午节吃粽子是中华民族的传统习俗.地区不同，制作的粽子形状也不同，黔西南州最出名的就是鲜肉的灰色粽子，其形状接近于正三棱锥（如图）.若正三棱锥的底面边长为2，高为1，则该三棱锥的侧面积为（）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
8. 如图，在 $△ A B C$ 中，2BD=CD，E为AC中点，AD和BE相交于点F，那么AF：DF=（）.

A、2 B、 $\frac{3}{2}$ C、3 D、4

查看试题解析

二、多选题

9. 复数 $z = \frac{1}{2} + \frac{3}{2} i$ ， i是虚数单位，则下列结论正确的是（）

A、z的实部是 $\frac{1}{2}$ B、z的共轭复数为 $\frac{3}{2} + \frac{1}{2} i$ C、z的实部与虚部之和为2 D、z在复平面内的对应点位于第一象限

查看试题解析
10. 样本容量为100的样本，其数据分布在 $[2 ， 18]$ 内，将样本数据分为4组： $[2 ， 6)$ ， $[6 ， 10)$ ， $[10 ， 14)$ ， $[14 ， 18]$ ，得到频率分布直方图如图所示，则下列说法中正确的是（　　）

A、样本数据分布在 $[6 ， 10)$ 内的频率为0.32 B、样本数据分布在 $[10 ， 14)$ 内的频数为40 C、样本数据分布在 $[2 ， 10)$ 内的频数为40 D、估计总体数据大约有 $10 %$ 分布在 $[10 ， 14)$ 内

查看试题解析
11. 如图，在正三棱柱 $A B C - A^{'} B^{'} C^{'}$ 中， $D$ 为棱 $A C$ 的中点， $A B = B B^{'} = 2$ ，则下列结论正确的是（）

A、 $B D ⊥ A C^{'}$ B、直线 $A C^{'}$ 与面 $A B C$ 所成角为45° C、线段 $B D = \sqrt{5}$ D、直线 $B D / /$ 面 $A^{'} B^{'} C^{'}$

查看试题解析
12. 对于任意 $△ A B C$ ， $\vec{A E} = 2 \vec{E C}$ ， $\vec{B D} = \frac{3}{4} \vec{D C}$ ，两直线AD，BE相交于点O，延长CO交AB于点F，则下列结论正确的是（）

A、 $\vec{C O} = \frac{3}{17} \vec{C A} + \frac{8}{17} \vec{C B}$ B、 $x \vec{O A} + y \vec{O B} + z \vec{O C} = \vec{0}$ ， $x ： y ： z = 3 ： 8 ： 7$ C、当 $∠ B A C = \frac{π}{3}$ ， $A B = 1$ ， $A C = 2$ 时，则 $c o s ∠ D O E = \frac{11 \sqrt{247}}{494}$ D、 $\frac{S_{△ D E F}}{S_{△ A B C}} = \frac{48}{231}$

查看试题解析

三、填空题

13. 计算： $s i n 60 ° c o s 30 ° - c o s 60 ° s i n 30 ° =$ .

查看试题解析
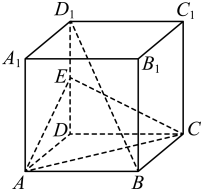
14. 已知 $\vec{a}$ 与 $\vec{b}$ 的夹角为60°， $| \vec{a} | = 2$ ， $| \vec{b} | = 1$ ， $\vec{a} \cdot \vec{b} =$ .

查看试题解析
15. 在不透明的袋子中装有5个大小质地完全相同的球，其中2个红球，3个黄球，从中随机摸出1个球，则事件“摸到红球”的概率为.

查看试题解析
16. 如图，在多面体 $A B C - A^{'} B^{'} C^{'}$ 中，已知 $A A^{'} = 2$ ， $A C = B^{'} C^{'} = 4$ ， $A C ⊥ C C^{^{'}}$ ，平面 $A A^{'} C^{'} C ⊥$ 平面 $B B^{'} C^{'} C$ ，四边形 $B B^{'} C^{'} C$ 是正方形，则点 $A$ 到平面 $A^{'} B C$ 的距离是.

查看试题解析

四、解答题

17. 已知函数 $f (x) = c o s 2 x + \sqrt{3} s i n 2 x$ ，

(1)、求 $f (x)$ 的最小正周期；

(2)、求 $f (x)$ 的最大值和最小值.

查看试题解析
18. 已知 $a ， b ， c$ 分别为 $△ A B C$ 三个内角 $A ， B ， C$ 的对边，且 $\sqrt{3} c o s A = s i n A$ ，

(1)、求 $A$ ；

(2)、若 $a = 2$ ，且 $b + c = 4$ ，求 $△ A B C$ 的面积.

查看试题解析
19. 中学阶段是学生身体发育最重要的阶段，长时间熬夜学习严重影响学生的身体健康．某校为了解甲、乙两班学生每周自我熬夜学习的总时长（单位：小时），分别从这两个班中随机抽取5名同学进行调查，得到他们最近一周自我熬夜学习的总时长的样本数据：
甲班
8
13
28
32
39
乙班
12
25
26
28
31
如果学生平均每周自我熬夜学习的总时长超过26小时，则称为“过度熬夜”．

(1)、请根据样本数据，分别估计甲、乙两班的学生平均每周自我熬夜学习时长的平均值；

(2)、从样本甲、乙两班所有“过度熬夜”的学生中任取2人，求这2人都来自甲班的概率．

查看试题解析
20. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ 是棱 $D D_{1}$ 的中点.

(1)、证明： $B D_{1} / /$ 平面 $A E C$ ；

(2)、若正方体棱长为2，求三棱锥 $D - A E C$ 的体积.

查看试题解析
21. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为正方形，侧面 $P A D$ 是正三角形，侧面 $P A D ⊥$ 底面 $A B C D$ ， $M$ 是 $P D$ 的中点．

(1)、求证： $A M ⊥$ 平面 $P C D$ ；

(2)、求侧面 $P B C$ 与底面 $A B C D$ 所成二面角的余弦值．

查看试题解析
22. 在① $a c o s B + b c o s A = 2 c c o s A$ ；② ${(s i n B - s i n C)}^{2} = s i n^{2} A - s i n B s i n C$ ；③ $S = \frac{1}{4} b (b s i n A + a t a n A c o s B)$ （其中 $S$ 为 $△ A B C$ 的面积）三个条件中任选一个补充在下面问题中，并作答.
在 $△ A B C$ 中，角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ， $a = 3 \sqrt{3}$ 且____.

(1)、求 $△ A B C$ 外接圆半径 $R$ ；

(2)、若 $△ A B C$ 为锐角三角形，求 $△ A B C$ 周长的取值范围.

查看试题解析

甲班	8	13	28	32	39
乙班	12	25	26	28	31