海南省2022-2023学年高一下学期学业水平诊断（二）数学试题

试卷更新日期：2023-08-03 类型：期末考试

进入出卷网下载

一、单选题

1. 已知复数 $z = \frac{5 i}{1 + 2 i}$ ，则 $\bar{z} =$ （）

A、 $1 + 2 i$ B、 $1 - 2 i$ C、 $2 + i$ D、 $2 - i$

查看试题解析

2. 每年4月15日为全民国家安全教育日，某学校党委组织党员学习《中华人民共和国国家安全法》，为了解党员学习的情况，随机抽取了部分党员，对他们一周的学习时间（单位：时）进行调查，统计数据如下表所示：

学习时间（时）	$[0 ， 2)$	$[2 ， 4)$	$[4 ， 6)$	$[6 ， 8)$	$[8 ， 10]$
党员人数	8	13	9	10	10

则从该校随机抽取1名党员，估计其学习时间不少于6小时的概率为（）

A、0.2 B、0.4 C、0.6 D、0.8

查看试题解析

3. 已知向量 $\vec{a} = (x ， 1)$ ， $\vec{b} = (1 ， - 2)$ ，且 $\vec{a} ⊥ \vec{b}$ ，则 $| \vec{a} - 2 \vec{b} | =$ （）

A、3 B、5 C、 $5 \sqrt{2}$ D、25

查看试题解析
4. 已知在四边形 $A B C D$ 中， $A B ∥ C D$ ， $A B ⊥ A D$ ，且 $A B = 2 C D = 2$ ， $A D = \sqrt{3}$ ，则将四边形 $A B C D$ 绕直线 $A D$ 旋转一周后所形成的几何体的侧面积为（）

A、 $\sqrt{6} π$ B、 $3 π$ C、 $6 π$ D、 $4 \sqrt{3} π$

查看试题解析
5. 已知 $0 < α < \frac{π}{2} < β < π$ ， $c o s α = \frac{3}{5}$ ， $s i n β = \frac{12}{13}$ ，则 $c o s (α + β) =$ （）

A、 $- \frac{63}{65}$ B、 $- \frac{33}{65}$ C、 $\frac{33}{65}$ D、 $\frac{63}{65}$

查看试题解析
6. 新海航大厦是中国唯一五星航空——海南航空集团总部办公楼，外形像张满的风帆，是海口市一个崭新的地标式建筑，某同学为测楼高 $A B$ ，选取了与楼基 $B$ 在同一水平面内的两个测量基点 $C$ 与 $D$ ，测得 $∠ B C D = 15 °$ ， $∠ B D C = 30 °$ ， $∠ A C B = 45 °$ ，再通过计算得楼高 $A B$ 为 $138 m$ ，则两个测量基点之间的距离 $C D$ 约为（）

A、159m B、195m C、207m D、239m

查看试题解析
7. 如图所示，正方形 $A B C D$ 的边长为2，点 $E$ ， $F$ ， $G$ 分别是边 $B C$ ， $C D$ ， $A D$ 的中点，点 $P$ 是线段 $E F$ 上的动点，则 $\vec{G P} \cdot \vec{A P}$ 的最小值为（）

A、 $\frac{23}{8}$ B、3 C、 $\frac{27}{8}$ D、48

查看试题解析
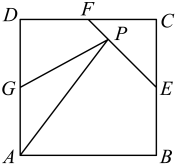8. 甲、乙两人每次射击命中目标的概率分别为 $\frac{2}{3}$ 与 $\frac{1}{2}$ ，且每次射击命中与否互不影响，现两人玩射击游戏，规则如下：每次由1人进行射击，若射击一次不中，则原射击人继续射击，若射击一次命中，则换对方接替射击，且第一次由甲射击.则前4次中甲恰好射击3次的概率为（）

A、 $\frac{2}{9}$ B、 $\frac{7}{27}$ C、 $\frac{8}{27}$ D、 $\frac{1}{3}$

查看试题解析

二、多选题

9. 已知一组数据为：3，4，6，7，7，5，5，4，5，4，则这组数据的（）

A、平均数为5 B、众数为5 C、中位数为5.5 D、方差为 $\frac{8}{5}$

查看试题解析
10. 下列说法正确的是（）

A、对任意向量 $\vec{a}$ ， $\vec{b}$ ，都有 $| \vec{a} \cdot \vec{b} | \leq | \vec{a} | | \vec{b} |$ B、对任意非零向量 $\vec{a}$ ， $\vec{b}$ ，都有 $| \vec{a} + \vec{b} | < | \vec{a} | + | \vec{b} |$ C、若向量 $\vec{a}$ ， $\vec{b}$ 满足 $(\vec{a} + \vec{b}) ⊥ (\vec{a} - \vec{b})$ ，则 $| \vec{a} | = | \vec{b} |$ D、若非零向量 $\vec{a}$ ， $\vec{b}$ 满足 $\vec{a} ⊥ \vec{b}$ ，则 $| \vec{a} + \vec{b} | = | | \vec{a} | - | \vec{b} | |$

查看试题解析
11. 如图所示，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $P$ 为线段 $B C_{1}$ 上的动点（不与点 $B$ 重合），若 $A B = B C = 1$ ， $C C_{1} = 2$ ，则（）

A、 $A P ⊥ A_{1} D$ B、三棱锥 $P - A D_{1} B_{1}$ 的体积为定值 C、异面直线 $B P$ 与 $A C$ 所成角的余弦值为 $\frac{\sqrt{10}}{10}$ D、二面角 $P - A B - C$ 的正切值为2

查看试题解析
12. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，则下列说法正确的是（）

A、若 $A = \frac{2 π}{3}$ ， $a = 3$ ， $A B$ 边上的高为 $\frac{3}{2}$ ，则 $△ A B C$ 为等腰三角形 B、若 $a = \sqrt{3}$ ， $b = 1$ ， $B = \frac{π}{6}$ ，则 $△ A B C$ 为直角三角形 C、若 $A = 2 C$ ， $s i n B = 2 s i n C$ ，则 $△ A B C$ 为直角三角形 D、若 $t a n A + t a n B + t a n C > 0$ ，则 $△ A B C$ 为锐角三角形

查看试题解析

三、填空题

13. 已知复数 $z = (a - i) (1 + i) (a \in R)$ 是纯虚数，则 $a =$ .

查看试题解析

14. 某学校有绘画、围棋、篮球三个兴趣小组，三个年级参加兴趣小组的学生人数如下表（每名同学只参加一个兴趣小组）：

	绘画组	围棋组	篮球组
高一	50	$m$	40
高二	30	40	20
高三	20	10	10

学校要对这三个兴趣小组的活动效果进行抽样调查，按各组人数的比例用分层随机抽样的方法，从这些学生中抽取30人，若围棋组被抽出10人，则 $m$ 的值为.

查看试题解析

15. 已知函数 $f (x) = A s i n (ω x + φ)$ 的部分图象如图所示，则 $f (- \frac{π}{4}) =$ .

查看试题解析
16. 已知正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 的高是底面边长的2倍，其外接球半径为 $\frac{2 \sqrt{3}}{3}$ ，点 $P$ 与 $Q$ 分别是侧棱 $B B_{1}$ ， $C C_{1}$ 上的动点，则 $A P + P Q + Q A_{1}$ 的最大值为.

查看试题解析

四、解答题

17. 如图所示，在四面体 $A B C D$ 中， $△ A B C$ 与 $△ A C D$ 均为等腰直角三角形， $A D = A C = B C = 1$ ， $B D = \sqrt{3}$ .

(1)、证明： $A D ⊥$ 平面 $A B C$ ；

(2)、若点 $E$ 在棱 $B D$ 上，且 $A E ⊥ B D$ ，求四面体 $A C D E$ 与四面体 $A B C E$ 的体积之比.

查看试题解析
18. 已知函数 $f (x) = s i n^{2} x - c o s^{2} x$ ，

(1)、若 $f (α) = \frac{1}{4}$ ，且 $α \in (0 ， \frac{π}{2})$ ，求 $f (α + \frac{π}{4})$ 的值；

(2)、求函数 $g (x) = \frac{f (x)}{2} - f (\frac{x}{2})$ 的最大值.

查看试题解析
19. 第31届世界大学生夏季运动会（简称大运会）将于2023年7月28日在四川成都开幕，这是中国西部城市第一次举办世界性综合运动会.为普及大运会相关知识，营造良好的赛事氛围，某学校举行“大运会百科知识”答题活动，并随机抽取了20名学生，他们的答题得分（满分100分）的频率分布直方图如图所示.

(1)、求频率分布直方图中 $a$ 的值及这20名学生得分的80%分位数；

(2)、若从样本中任选2名得分在 $[50 ， 70)$ 内的学生，求这2人中恰有1人的得分在 $[60 ， 70)$ 内的概率

查看试题解析
20. 在如图所示的电路中， $K_{1}$ 、 $K_{2}$ 、 $K_{3}$ 、 $K_{4}$ 四个开关闭合的概率分别为 $\frac{3}{4}$ 、 $\frac{2}{3}$ 、 $\frac{1}{2}$ 、 $\frac{1}{2}$ ，且各个开关是否闭合是相互独立的.

(1)、求四个开关均断开的概率；

(2)、求电路为通路的概率

查看试题解析
21. 已知 $△ A B C$ 的内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ， $c = a c o s B + \frac{\sqrt{3}}{3} b s i n A$ .

(1)、求 $A$ ；

(2)、若 $a = \sqrt{3}$ ，求 $B C$ 边上的中线 $A M$ 的最大值.

查看试题解析
22. 如图，在正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B = 1$ ， $A A_{1} = \sqrt{2}$ ， $E$ 、 $F$ 分别为 $A_{1} C_{1}$ 、 $B_{1} C$ 的中点.

(1)、求证： $E F / /$ 平面 $A_{1} B C$ ；

(2)、求点 $A$ 到平面 $A_{1} B C$ 的距离；

(3)、求 $E F$ 与平面 $A C C_{1} A_{1}$ 所成的角的大小.

查看试题解析