安徽省安庆、池州、铜陵三市2022-2023学年高一下学期联合期末检测数学试题

试卷更新日期：2023-08-03 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | y = l n (x - 1)} ， B = {x | x^{2} + 2 x - 3 \geq 0}$ ，则 $A ∩ B =$ （）

A、 $(1 ， 3)$ B、 $(1 ， + \infty)$ C、 $[3 ， + \infty)$ D、 $[- 1 ， 1)$

查看试题解析
2. 已知a，b均为实数，复数： $z = a^{2} - b + (b - 2 a) i$ ，其中i为虚数单位，若 $z < 3$ ，则a的取值范围为（）

A、 $(- 1 ， 3)$ B、 $(- \infty ， - 1) \cup (3 ， + \infty)$ C、 $(- \infty ， - 3) ∪ (1 ， + \infty)$ D、 $(- 3 ， 1)$

查看试题解析
3. 如图，是水平放置的 $△ O A B$ 用斜二测画法得到的直观图 $△ O^{'} A^{'} B^{'}$ （其中 $∠ x^{'} O^{'} y^{'} ＝ 45 °$ ），若 $A^{'} B^{'} ⊥ x^{'}$ 轴， $O^{'} A^{'} = 2 ， A^{'} B^{'} = 2 \sqrt{2}$ ，则 $△ O A B$ 的面积为（）

A、 $2 \sqrt{2}$ B、4 C、8 D、 $4 \sqrt{2}$

查看试题解析
4. 唐代以来，牡丹之盛，以“洛阳牡丹甲天下”的美名流传于世．唐朝诗人白居易“花开花落二十日，一城之人皆若狂”和刘禹锡“唯有牡丹真国色，花开时节动京城”的诗句正是描写洛阳城的景象．已知根据花瓣类型可将牡丹分为单瓣类、重瓣类、千瓣类三类，现有牡丹花n朵，千瓣类比单瓣类多30朵，采用分层抽样方法从中选出12朵牡丹进行观察研究，其中单瓣类有4朵，重瓣类有2朵，千瓣类有6朵，则n＝（）

A、360 B、270 C、240 D、180

查看试题解析
5. 在△ABC中，内角A，B，C的对边分别为a，b，c，若△ABC为钝角三角形，且 $a = 6 ， b = 8$ ，则c的取值不可能的是（）

A、3 B、4 C、9 D、12

查看试题解析
6. 已知向量 $\vec{a} = (3 ， - 1) ， \vec{b} = (- 1 ， 2)$ ，则向量 $\vec{a}$ 在向量 $\vec{b}$ 上的投影向量是（）

A、 $(1 ， - 2)$ B、 $(- 1 ， 2)$ C、 $(\sqrt{5} ， - 2 \sqrt{5})$ D、 $(- \sqrt{5} ， 2 \sqrt{5})$

查看试题解析
7. 某校通过统计学生在校的5次模考数学成绩（分数均为整数）决定该学生是否适合进行数学竞赛培训．规定：“5次模考成绩均不低于140分”，现有甲、乙、丙三位同学5次模考成绩，则根据以下数据能确定适合数学竞赛培训的学生有（）
甲：众数为140，中位数为145；
乙：中位数为145，极差为6；
丙：均值为143，其中一次成绩为145，方差为1.6．

A、甲乙 B、甲丙 C、乙丙 D、甲乙丙

查看试题解析
8. 设函数 $f (x) = {\begin{array}{l} x^{2} ， x \leq 1 \\ | l o g_{2} (x - 1) | ， x > 1 \end{array}$ ，若 $f (x_{1}) = f (x_{2}) = f (x_{3}) = f (x_{4})$ （其中 $x_{1} < x_{2} < x_{3} < x_{4}$ ），则 $\frac{4}{x_{4} + 1} + (x_{1} + x_{2} + 2) x_{3}$ 的取值范围是（）

A、 $(3 ， \frac{10}{3})$ B、 $(4 ， \frac{16}{3})$ C、 $(3 ， \frac{10}{3}]$ D、 $[4 ， \frac{16}{3})$

查看试题解析

二、多选题

9. 已知m，n为两条不同的直线， $α ， β$ 为两个不同的平面，命题“若____，则m⊥n”是真命题，则横线上可以是下列选项中的（）

A、 $m ⊥ α ， n ⊥ β$ ，且 $α ∥ β$ B、 $m ⊥ α ， n ∥ β$ ，且 $α ∥ β$ C、 $α ∥ β ， m \subset α ， n \subset β$ D、 $m ⊥ α ， n ⊥ β$ ，且 $α ⊥ β$

查看试题解析
10. 欧拉公式 $e^{i x} = c o s x + i s i n x$ （e为自然对数的底数，i为虚数单位）是由瑞士著名数学家欧拉创立，该公式建立了三角函数与指数函数的关系，在复变函数论中占有非常重要的地位，被誉为“数学中的天桥”，在复数范围内关于x的方程 $x^{2} + a x + b = 0 (a ， b \in R)$ 的两根为 $z_{1} ， z_{2}$ ，其中 $z_{1} = \sqrt{2} e^{\frac{π}{4} i}$ ，则下列结论中正确的是（）

A、复数z＝a＋bi对应的点在第一象限 B、 $| a + b i | = 2 \sqrt{2}$ C、 $z_{2} = 1 - i$ D、 $| z_{1} z_{2} | = | z_{1} | | z_{2} |$

查看试题解析
11. 在 $△ A B C$ 中，内角A，B，C所对的边分别为a，b．c．若 $A = \frac{2 π}{3}$ ，角A的平分线 $A D$ 交 $B C$ 于点D， $A D = 2$ ， $b = 6$ ，则以下结论正确的是（）

A、 $c = 3$ B、 $B D = 2 C D$ C、 $△ A B C$ 的面积为 $\frac{9 \sqrt{3}}{2}$ D、 $a = 3 \sqrt{5}$

查看试题解析
12. 如图1，将正方体沿交于同一顶点的三条棱的中点截去一个三棱锥，如此共可截去八个三棱锥，截取后的剩余部分称为“阿基米德多面体”．阿基米德多面体是一个有十四个面的半正多面体，其中八个面为正三角形，六个面为正方形、它们的边长都相等，又称这样的半正多面体为二十四等边体．如图2，现有一个边长为2的二十四等边体、则关于该二十四等边体说法正确的是（）

A、该二十四等边体的表面积为 $24 + 8 \sqrt{3}$ B、共有8条棱所在直线与直线AB异面，且所成角为 $\frac{π}{3}$ C、任意两个有公共顶点的三角形所在平面的夹角余弦值均为 $\frac{1}{3}$ D、该二十四等边题的外接球的体积为 $\frac{32}{3} π$

查看试题解析

三、填空题

13. 某校高三年级10次模考中甲同学的数学成绩从小到大依次排列为94，96，98，98，100，101，101，102，102，103，则甲同学在这10次模考中数学成绩的第40百分位数为．

查看试题解析
14. 若 $c o s (\frac{π}{3} + α) = \frac{1}{3}$ ，且 $\frac{π}{2} < α < \frac{3 π}{2}$ ，则 $c o s (\frac{π}{6} - α) =$ ．

查看试题解析
15. 已知事件A，B，C两两相互独立，若 $P (A B) = \frac{2}{9} ， P (B \bar{C}) = \frac{1}{3} ， P (A \bar{C}) = \frac{1}{6}$ ，则P（A）＝．

查看试题解析
16. 如图是甲烷的球棍结构，它的分子结构为正四面体结构（正四面体是每个面都是正三角形的四面体），碳原子位于正四面体的中心，4个氢原子分别位于正四面体的4个顶点．已知相邻的两个氢原子之间的距离为7，若不计原子大小，该正四面体内放入一个圆柱，使得圆柱的下底面在正四面体的底面，则当该圆柱的表面积取得最大值时，圆柱的底面半径为．

查看试题解析

四、解答题

17. 如图，在 $△ A B C$ 中， $A B = 6$ ， $B C = 2 \sqrt{2}$ ， $∠ A B C = \frac{3}{4} π$ ，点P在线段AC上，且有 $\vec{A P} = 3 \vec{P C}$ ．

(1)、用向量 $\vec{B A} ， \vec{B C}$ 表示 $\vec{B P}$ ；

(2)、求 $\vec{B P} \cdot \vec{A C}$ 的值．

查看试题解析
18. 为提高全民的身体素质，某市体育局举行“万人健步走”活动，体育局通过市民上传微信走步截图的方式统计上传者每天的步数，现从5月20日参加活动的全体市民中随机抽取了100人的走步数组成样本进行研究，并制成如图所示的频率分布直方图（步数单位：千步）．

(1)、求a的值，并根据直方图估计5月20日这100位市民走步数的平均数（同一组中的数据用该组区间中点值代表）；

(2)、按分层抽样的方式在 $[23 ， 27)$ 和 $[27 ， 31]$ 两组中抽取5人，再从这5人中随机抽取2人进行走步路线调查，求这2人步数都在 $[27 ， 31]$ 的概率．

查看试题解析
19. 如图，在四棱锥P－ABCD中，底面ABCD是菱形，AB＝2， $∠ A B C = \frac{π}{3}$ ， △PAB是正三角形，平面PAB⊥平面ABCD，点Q是线段PC的中点．

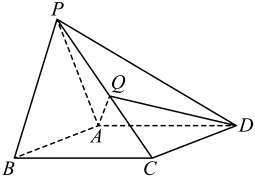(1)、求三棱锥Q－PAD的体积；

(2)、求平面PBC与平面BCD夹角的余弦值．

查看试题解析
20. 在 $△ A B C$ 中，内角A，B，C的对边分别为a，b，c，若 $a = \frac{\sqrt{3}}{3} b ， t a n C = \frac{c c o s A}{a + c s i n A}$ ．

(1)、求角B的大小；

(2)、若 $△ A B C$ 的外接圆周长为 $2 \sqrt{3} π$ ，求BC边上的中线长.

查看试题解析
21. 如图，在斜三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，四边形 $A B B_{1} A_{1}$ 是边长为2的菱形， $∠ A_{1} A B = \frac{π}{3}$ ， $△ A B C$ 为正三角形，平面 $A B B_{1} A_{1} ⊥$ 平面 $A B C$ ，点P是棱 $C C_{1}$ 的中点．

(1)、求证：平面 $P B_{1} A ⊥$ 平面 $A B B_{1} A_{1}$ ；

(2)、求 $P A_{1}$ 与平面 $P B_{1} A$ 所成角．

查看试题解析
22. 已知函数 $f (x) = l g (10 0^{x} + a) - x (a > 0)$ ．

(1)、当函数 $f (x)$ 是偶函数时，解不等式： $f (x) < l g \frac{5}{2}$ ；

(2)、若函数 $g (x) = f (x) - l g (1 - 3 \times 1 0^{x})$ 有两个零点，求实数a的取值范围．

查看试题解析