黑龙江省哈尔滨市2022-2023学年高一下学期期末数学试题

试卷更新日期：2023-08-03 类型：期末考试

进入出卷网下载

一、单选题

1. 若复数 $z = \frac{a + i}{1 - i}$ 是纯虚数，则实数a的值是（）

A、1 B、0 C、 $- 1$ D、 $- 2$

查看试题解析
2. 某企业职工有高级职称的共有15人，现按职称用分层抽样的方法抽取30人，有高级职称的3人，则该企业职工人数为（）

A、150 B、130 C、120 D、100

查看试题解析
3. （理科）在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，E，F分别为棱BC和棱 $C C_{1}$ 的中点，则异面直线AC和EF所成的角为（）

A、90° B、60° C、45° D、30°

查看试题解析
4. 设 $\vec{e_{1}}$ ， $\vec{e_{2}}$ 是两个不共线的向量，若向量 $\vec{m} = - \vec{e_{1}} + k \vec{e_{2}} (k \in R)$ 与向量 $\vec{n} = \vec{e_{2}} - \vec{e_{1}}$ 共线，则 $k =$ （）

A、0 B、 $\frac{1}{2}$ C、1 D、2

查看试题解析
5. 抛掷一枚质地均匀的正方体骰子，观察向上一面的点数，则下列是互斥事件但不是对立事件的是（）

A、“大于3点”与“不大于3点” B、“大于3点”与“小于2点” C、“大于3点”与“小于4点” D、“大于3点”与“小于5点”

查看试题解析
6. 已知三个不同的平面 $α ， β ， γ$ 和直线 $m ， n$ ，若 $α ∩ γ = m$ ， $β ∩ γ = n$ ，则“ $α / / β$ ”是“ $m / / n$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
7. 已知平面向量 $\vec{a} = (1 ， λ)$ ， $\vec{b} = (- 2 ， 1)$ ，则下列说法正确的是（）

A、若 $λ = 0$ ，则 $| \vec{a} + \vec{b} | = 2$ B、若 $\vec{a} ∥ \vec{b}$ ，则 $λ = - 2$ C、若 $\vec{a}$ 与 $\vec{b}$ 的夹角为钝角，则 $λ < 2$ D、若 $λ = - 1$ ，则 $\vec{a}$ 在 $\vec{b}$ 上的投影向量为 $- \frac{3}{5} \vec{b}$

查看试题解析
8. 在 $△ A B C$ 中，已知 $s i n A + s i n B = c o s A + c o s B$ ，则 $△ A B C$ 的形状一定是（）

A、等腰三角形 B、直角三角形 C、等边三角形 D、等腰或直角三角形

查看试题解析

二、多选题

9. 下列各复数中，模长为1的有（）

A、1 B、 $2 - i$ C、 $1 - i$ D、 $i$

查看试题解析
10. 为了加深师生对党史的了解，激发广大师生知史爱党、知史爱国的热情，某校举办了“学党史、育文化”暨“喜迎党的二十大”党史知识竞赛，并将1000名师生的竞赛成绩（满分100分，成绩取整数）整理成如图所示的频率分布直方图，则下列说法正确的是（）

A、 $a$ 的值为0.05 B、估计成绩低于60分的有25人 C、估计这组数据的众数为75 D、估计这组数据的第85百分位数为86

查看试题解析
11. 在锐角 $△ A B C$ 中，内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，若 $a - b = 2 b c o s C$ ，则（）

A、 $C = 2 B$ B、 $B$ 的取值范围是 $(\frac{π}{6} ， \frac{π}{4})$ C、 $B = 2 C$ D、 $\frac{c}{b}$ 的取值范围是 $(\sqrt{2} ， \sqrt{3})$

查看试题解析
12. 如图，将一副三角板拼成平面四边形，将等腰直角△ABC沿BC向上翻折，得三棱锥 $A - B C D$ ．设CD＝2，点E，F分别为棱BC，BD的中点，M为线段AE上的动点．下列说法正确的是（）

A、存在某个位置，使 $A B ⊥ C D$ B、存在某个位置，使 $A C ⊥ B D$ C、当三棱锥 $A - B C D$ 体积取得最大值时，AD与平面ABC成角的正切值为 $\frac{\sqrt{6}}{3}$ D、当AB＝AD时，CM+FM的最小值为 $\sqrt{4 + 2 \sqrt{2}}$

查看试题解析

三、填空题

13. 某工厂现对一批零件的性能进行抽检，第一次检测每个零件合格的概率是0.8，不合格的零件重新加工后进行第二次检测，第二次检测合格的概率是0.9，如果第二次检测仍不合格，则作报废处理.则每个零件报废的概率为.

查看试题解析
14. 在 $△ A B C$ 中， $\vec{B E} = λ \vec{E C}$ ，且 $\vec{A E} = \frac{3}{4} \vec{A B} + \frac{1}{4} \vec{A C}$ ，则 $λ =$ ．

查看试题解析
15. 一艘轮船航行到A处时看灯塔B在A的北偏东 $75 °$ ，距离 $12 \sqrt{6}$ 海里，灯塔C在A的北偏西 $30 °$ ，距离为 $12 \sqrt{3}$ 海里，该轮船由A沿正北方向继续航行到D处时再看灯塔B在其南偏东 $60 °$ 方向，则 $c o s ∠ C D A =$ ．

查看试题解析
16. 四面体ABCD中，AB⊥平面BCD，CD⊥BC，CD=BC=2，若二面角A-CD-B的大小为60°，则四面体ABCD的外接球的体积为．

查看试题解析

四、解答题

17. 已知 $| \vec{a} | = 2$ ， $| \vec{b} | = 4$ ， $\vec{a}$ 与 $\vec{b}$ 的夹角为 $θ$ .

(1)、若 $\vec{a} / / \vec{b}$ ，求 $\vec{a} \cdot \vec{b}$ ；

(2)、若 $\vec{a} + \vec{b}$ 与 $\vec{a}$ 垂直，求 $θ$ .

查看试题解析
18. 某小区所有248户家庭人口数分组表示如下：
家庭人口数
1
2
3
4
5
6
7
家庭数
21
29
49
50
46
35
18

(1)、求该小区家庭人口数的中位数；

(2)、求该小区家庭人口数的方差.（精确到0.1）

查看试题解析
19. 在 $△ A B C$ 中，角A，B，C的对边分别为a，b，c，且 $2 a s i n (\frac{π}{2} - C) = 2 b + c$ .

(1)、求角A；

(2)、若 $△ A B C$ 的面积为 $\frac{3 \sqrt{3}}{4}$ ，求a的最小值.

查看试题解析
20. 如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B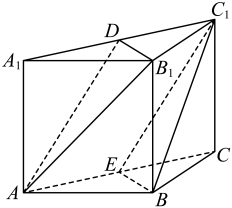 = B C = A A_{1} = 1$ ， $∠ A B C = 90 °$ ， D，E分别是棱 $A_{1} C_{1}$ ， AC的中点．

(1)、判断多面体 $A B E D B_{1} C_{1}$ 是否为棱柱并说明理由；

(2)、求多面体 $A B E D B_{1} C_{1}$ 的体积；

(3)、求证：平面 $B C_{1} E / /$ 平面AB₁D．

查看试题解析
21. 一只口袋里有形状、大小、质地都相同的4个小球，这4个小球上分别标记着数字1，2，3，4．甲、乙、丙三名学生约定：
（i）每人不放回地随机摸取一个球；
（ii）按照甲、乙、丙的次序依次摸取；
（iii）谁摸取的球的数字最大，谁就获胜．
用有序数组 $(a ， b ， c)$ 表示这个试验的基本事件，例如： $(1 ， 4 ， 3)$ 表示在一次试验中，甲摸取的球的数字是1，乙摸取的球的数字是4，丙摸取的球的数字是3．

(1)、列出样本空间，并指出样本空间中样本点的总数；

(2)、求甲获胜的概率；

(3)、写出乙获胜的概率，并指出甲、乙、丙三名同学获胜的概率与其摸取的次序是否有关．

查看试题解析
22. 如图，已知四棱锥P－ABCD的底面为矩形，AB＝PD＝2， $A D = 2 \sqrt{2}$ ， O是AD的中点，PO⊥平面ABCD．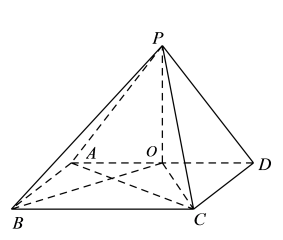

(1)、求证：AC⊥平面POB；

(2)、设平面PAB与平面PCD的交线为l．
①求证： $l ∥ A B$ ；
②求l与平面PAC所成角的大小．

查看试题解析

家庭人口数	1	2	3	4	5	6	7
家庭数	21	29	49	50	46	35	18