2023-2024学年苏科版数学九年级上册2.8圆锥的侧面积 同步练习
试卷更新日期：2023-08-03 类型：同步测试
一、选择题
-
1. 如图，把一个高分米的圆柱的底面分成许多相等的扇形，然后把圆柱切开，拼成一个与它等底等高的近似长方体，它的表面积比圆柱体的表面积增加了平方分米．原来这个圆柱的体积是立方分米．（ ）
A、 B、 C、 D、2. 一个几何体的三视图如下，则这个几何体的表面积是（ ）
A、 B、 C、 D、3. 某几何体的三视图如图所示，该几何体的母线长是（ ）
A、5 B、10 C、12 D、134. 如图，斗笠是一种遮挡阳光和蔽雨的编结帽，它可近似看成一个圆锥，已知该斗笠的侧面积为550πcm2 ， AB是斗笠的母线，长为25cm，AO为斗笠的高，BC为斗笠末端各点所在圆的直径，则OC的值为（ ）
A、22 B、23 C、24 D、255. 如图，圆锥底面圆半径为7cm，高为24cm，则它侧面展开图的面积是（ ）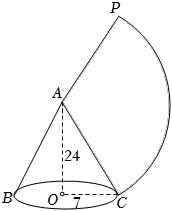
A、 cm2 B、 cm2 C、175πcm2 D、350πcm26. 如图是某工件的三视图，则此工件的表面积为（ ）
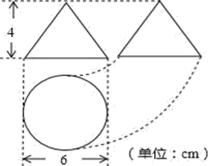A、cm2 B、cm2 C、cm2 D、cm27. 一个几何体的三视图如下：其中主视图和左视图都是腰长为4，底边为2的等腰三角形，则这个几何体侧面展开图的面积和圆心角分别是（ ）
A、4π60° B、4π90° C、2π90° D、8π60°8. 已知圆锥的底面积为 ， 高为 ， 则圆锥的侧面积是（ ）A、 B、 C、 D、9. 如图，将圆锥沿一条母线剪开并展平，得到一个扇形，若圆锥的底面圆的半径 ， 扇形的圆心角 ， 则该圆锥母线的长为（ ）
A、8 B、6 C、4 D、310. 如图，在四边形ABCD中，AB∥CD，∠A=90°，AB=5，CD=2．以A为圆心，AD为半径的圆与BC边相切于点M，与AB交于点E，将扇形A﹣DME剪下围成一个圆锥，则圆锥的高为（ ）
A、1 B、4 C、 D、11. 《九章算术》商功章有题：一圆柱形谷仓，高1丈3尺3 寸，容纳米2000斛（1丈=10尺，1尺=10寸，斛为容积单位，1斛≈1.62立方尺，π=3），则圆柱底周长约为（注：圆柱体的体积=底面积×高）（ ）
A、1丈3尺 B、5丈4尺 C、9丈2尺 D、48丈6尺12. 一个圆锥的侧面积是底面积的4倍，则圆锥侧面展开图的扇形的圆心角是（ ）A、60° B、90° C、120° D、180°二、填空题
-
13. 已知圆锥的侧面展开图是一个半圆，则这个圆锥的侧面积与底面积的比是 ．14. 数学活动课上，某同学制作了一顶圆锥形纸帽．若圆锥的底面圆的半径为1分米，母线长为4分米，则该圆锥的高为分米．15. 如图，圆锥形烟囱帽的底面半径为 ， 母线长为 ， 则烟囱帽的侧面积为 ． （结果保留）
16. 如图（1），在正方形铁皮上剪下一个圆形和扇形，使之恰好围成如图（2）所示的一个圆锥模型，则圆的半径r与扇形的半径R之间的关系为 ．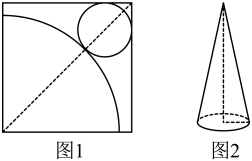
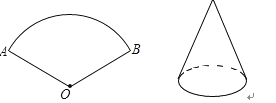
17. 圆锥的底面周长为 ，母线长为2，点P是母线OA的中点，一根细绳（无弹性）从点P绕圆锥侧面一周回到点P，则细绳的最短长度为 ．18.如图，将弧长为6π，圆心角为120°的圆形纸片AOB围成圆锥形纸帽，使扇形的两条半径OA与OB重合（粘连部分忽略不计）则圆锥形纸帽的高是 ．
三、解答题
-
19. 在数学实验课上，小莹将含角的直角三角尺分别以两个直角边为轴旋转一周，得到甲、乙两个圆锥，并用作图软件Geogebra画出如下示意图
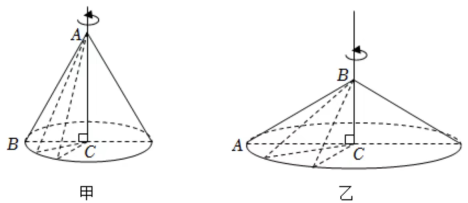
小亮观察后说：“甲、乙圆锥的侧面都是由三角尺的斜边旋转得到，所以它们的侧面积相等．”
你认同小亮的说法吗？请说明理由．
20. “赶陀螺”是一项深受人们喜爱的民族性运动，如图所示是一个陀螺的立体结构图.已知底面圆的直径 ，圆柱体部分的高 ，圆锥体部分的高 ，求出这个陀螺的表面积（结果保留 ）.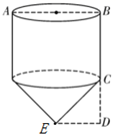
21. 如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行下列操作：
(1)、请在图中确定该圆弧所在圆心D点的位置 ， D点坐标为；(2)、连接AD、CD，求⊙D的半径及扇形DAC的圆心角度数；(3)、若扇形DAC是某一个圆锥的侧面展开图，求该圆锥的底面半径．四、综合题
-
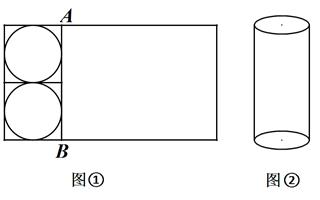
22. 用如图所示的甲、乙、丙木板做一个长、宽、高分别为a厘米，b厘米，h厘米的长方体有盖木箱（a>b），其中甲刚好能做成箱底和一个长侧面，乙刚好能做成一个长侧面和一个短侧面，丙刚好能做成箱盖和一个短侧面。
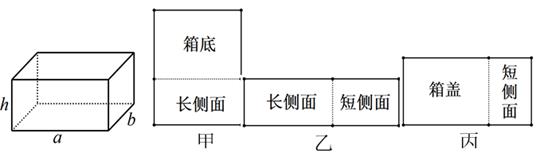(1)、填空：用含a、b、h的代数式表示以下面积：甲的面积；乙的面积；丙的面积.
(2)、当h=20cm时，若甲的面积比丙的面积大200cm2 ， 乙的面积为1400cm2 ， 求a和b的值；(3)、现将一张长、宽分别为a厘米、b厘米的长方形纸板（如图①）分割成两个小长方形。左侧部分刚好分割成两个最大的等圆，和右侧剩下部分刚好做成一个圆柱体模型（如图②），且这样的圆柱体模型的高刚好与木箱的高相等。问：一个上述长方体木箱中最多可以放个这样的圆柱体模型。