2023-2024学年苏科版数学九年级上册2.7弧长及扇形面积 同步练习
试卷更新日期:2023-08-03 类型:同步测试
一、选择题
-
1. 已知扇形的半径为6,圆心角为 , 则此扇形的弧长是( )A、4 B、2 C、 D、2. 如图,是半圆的直径,、是半圆上两点,且满足 , , 则的长为( )
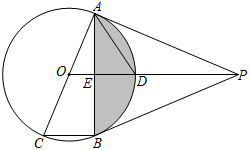
 A、 B、 C、 D、3. 如图,是的直径,弦与垂直,垂足为点E,连接并延长交于点 , , , 则图中阴影部分的面积为( )
A、 B、 C、 D、3. 如图,是的直径,弦与垂直,垂足为点E,连接并延长交于点 , , , 则图中阴影部分的面积为( ) A、 B、 C、 D、4. 勒洛三角形是分别以等边三角形的顶点为圆心,以其边长为半径作圆弧,由三段圆弧组成的曲边三角形.如图,该勒洛三角形绕其中心旋转一定角度后能与自身重合,则该角度可以为( )
A、 B、 C、 D、4. 勒洛三角形是分别以等边三角形的顶点为圆心,以其边长为半径作圆弧,由三段圆弧组成的曲边三角形.如图,该勒洛三角形绕其中心旋转一定角度后能与自身重合,则该角度可以为( ) A、 B、 C、 D、5. 【阅读理解】在求阴影部分面积时,常常会把原图形的一部分割下来补在图形中的另一部分,使其成为基本规则图形,从而使问题得到解决,这种方法称为割补法.如图1,C是半圆O的中点,欲求阴影部分面积,只需把弓形BC割下来,补在弓形处,则 .
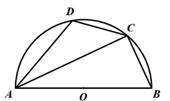
A、 B、 C、 D、5. 【阅读理解】在求阴影部分面积时,常常会把原图形的一部分割下来补在图形中的另一部分,使其成为基本规则图形,从而使问题得到解决,这种方法称为割补法.如图1,C是半圆O的中点,欲求阴影部分面积,只需把弓形BC割下来,补在弓形处,则 .
【拓展应用】如图2,以为直径作半圆O,C为的中点,连接 , 以为直径作半圆P,交于点D.若 , 则图中阴影部分的面积为( )
A、 B、 C、 D、6. 如图,在4×4的正方形网格中,若将△ABC绕着点A逆时针旋转得到△AB′C′,则 的长为( ) A、π B、 C、7 D、67. 如果一个扇形的弧长等于它的半径的 倍,那么此扇形称为“优雅扇形”,则半径为2的“优雅扇形”的面积为( )A、π B、 C、 π D、28. 如图,用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则图中阴影部分面积( )
A、π B、 C、7 D、67. 如果一个扇形的弧长等于它的半径的 倍,那么此扇形称为“优雅扇形”,则半径为2的“优雅扇形”的面积为( )A、π B、 C、 π D、28. 如图,用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则图中阴影部分面积( )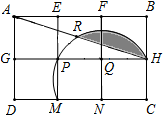 A、π﹣ B、π﹣5 C、2π﹣5 D、3π﹣29. 中国美食讲究色香味美,优雅的摆盘造型也会让美食錦上添花。图1中的摆盘,其形状是扇形的一部分,图2是其几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12cm,C,D两点之间的距离为4cm,圆心角为60°,则图中摆盘的面积是( )
A、π﹣ B、π﹣5 C、2π﹣5 D、3π﹣29. 中国美食讲究色香味美,优雅的摆盘造型也会让美食錦上添花。图1中的摆盘,其形状是扇形的一部分,图2是其几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12cm,C,D两点之间的距离为4cm,圆心角为60°,则图中摆盘的面积是( ) A、80π cm2 B、40π cm2 C、24π cm2 D、2π cm210. 如图,AB是⊙o直径,M,N是 上两点,C是 上任一点,∠ACB角平分线交⊙o于点D,∠BAC的平分线交CD于点E,当点C从M运动到N时,C、E两点的运动路径长之比为( )
A、80π cm2 B、40π cm2 C、24π cm2 D、2π cm210. 如图,AB是⊙o直径,M,N是 上两点,C是 上任一点,∠ACB角平分线交⊙o于点D,∠BAC的平分线交CD于点E,当点C从M运动到N时,C、E两点的运动路径长之比为( )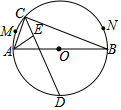 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,用一个半径为6cm的定滑轮拉动砝码上升(假设绳索足够长且粗细不计,与滑轮之间无滑动),若滑轮旋转了 , 则砝码上升了cm.(结果保留)
 12. 在2×2的正方形网格中,每个小正方形的边长为1.以点O为圆心,2为半径画弧,交图中网格线于点A,B,则扇形AOB的面积是.
12. 在2×2的正方形网格中,每个小正方形的边长为1.以点O为圆心,2为半径画弧,交图中网格线于点A,B,则扇形AOB的面积是.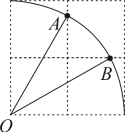 13. 如图,在中, , , , 将绕点A逆时针旋转后得到 , 点B经过的路径为 , 则图中阴影部分的面积为 .
13. 如图,在中, , , , 将绕点A逆时针旋转后得到 , 点B经过的路径为 , 则图中阴影部分的面积为 . 14. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠D=110°,则 的长为.
14. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠D=110°,则 的长为. 15. 已知扇形的面积为cm2 , 圆心角为 , 则该扇形的弧长是.16. 如图,正方形的边长为2,以A为圆心,长为半径画.以D为圆心,长为半径画 , 形成如图“杯子”样的阴影部分,则阴影部分的面积为.
15. 已知扇形的面积为cm2 , 圆心角为 , 则该扇形的弧长是.16. 如图,正方形的边长为2,以A为圆心,长为半径画.以D为圆心,长为半径画 , 形成如图“杯子”样的阴影部分,则阴影部分的面积为. 17. 如图,半径为4cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设 的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为.
17. 如图,半径为4cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设 的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为.
三、解答题
-
18. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,的三个顶点坐标分别为 .

( 1 )画出关于x轴对称的 , 并写出点的坐标;
( 2 )画出绕点O顺时针旋转后得到的 , 并写出点的坐标;
( 3 )在(2)的条件下,求点A旋转到点所经过的路径长(结果保留).
19. 一张圆心角为45°的扇形纸板和圆形纸板按如图方式各剪得一个正方形,边长都为1,求扁形纸板和圆形纸板的面积比. 20. 如图, 两两不相交,且半径都是 .求图中三个扇形(即阴影部分)的面积之和.
20. 如图, 两两不相交,且半径都是 .求图中三个扇形(即阴影部分)的面积之和.
四、综合题
-
21. 已知,为的弦,且.
 (1)、如图1,若 , 求阴影部分的面积;(2)、如图2,若点C为的中点,点D为的中点.请仅用无刻度的直尺过点B作的的切线.
(1)、如图1,若 , 求阴影部分的面积;(2)、如图2,若点C为的中点,点D为的中点.请仅用无刻度的直尺过点B作的的切线.