2023-2024学年苏科版数学九年级上册2.6正多边形与圆 同步练习
试卷更新日期:2023-08-03 类型:同步测试
一、选择题
-
1. 如图, , 为的两条弦,连结 , , 点为的延长线上一点.若 , 则为( )
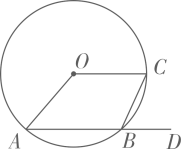 A、 B、 C、 D、2. 如图,正五边形内接于 , 点F在弧上.若 , 则的大小为( )
A、 B、 C、 D、2. 如图,正五边形内接于 , 点F在弧上.若 , 则的大小为( )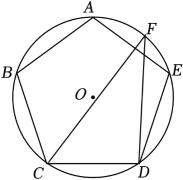 A、38° B、42° C、48° D、58°3. 下列图形中,正多边形内接于半径相等的圆,其中正多边形周长最小的是( )A、
A、38° B、42° C、48° D、58°3. 下列图形中,正多边形内接于半径相等的圆,其中正多边形周长最小的是( )A、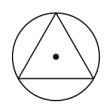 B、
B、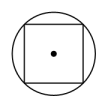 C、
C、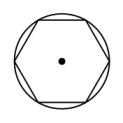 D、
D、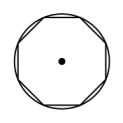 4. 如图,正六边形ABCDEF内接于 ,已知 的 半径为2,则圆心O到边AB的距离是( )
4. 如图,正六边形ABCDEF内接于 ,已知 的 半径为2,则圆心O到边AB的距离是( )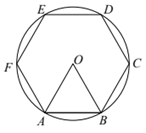 A、2 B、1 C、 D、5. 如图,正五边形 内接于 ,点 是劣弧 上一点(点 不与点 重合),则 ( )
A、2 B、1 C、 D、5. 如图,正五边形 内接于 ,点 是劣弧 上一点(点 不与点 重合),则 ( ) A、 B、 C、 D、6. 如图,正方形ABCD内接于 ,点P在 上,则 的度数为( )
A、 B、 C、 D、6. 如图,正方形ABCD内接于 ,点P在 上,则 的度数为( )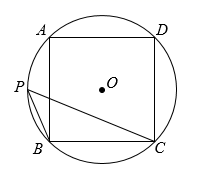 A、 B、 C、 D、7. 已知⊙O的半径是2,一个正方形内接于⊙O,则这个正方形的边长是( )A、2 B、2 C、 D、48. 正多边形的内切圆与外接圆的半径之比为 ,则这个正多边形为( )A、正十二边形 B、正六边形 C、正四边形 D、正三角形9. 如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
A、 B、 C、 D、7. 已知⊙O的半径是2,一个正方形内接于⊙O,则这个正方形的边长是( )A、2 B、2 C、 D、48. 正多边形的内切圆与外接圆的半径之比为 ,则这个正多边形为( )A、正十二边形 B、正六边形 C、正四边形 D、正三角形9. 如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )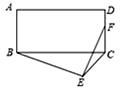 A、 B、4 C、5 D、10. 将边长为3cm的正三角形各边三等分,以这六个分点为顶点构成一个正六边形,则这个正六边形的面积为( )A、cm2 B、cm2 C、cm2 D、cm2
A、 B、4 C、5 D、10. 将边长为3cm的正三角形各边三等分,以这六个分点为顶点构成一个正六边形,则这个正六边形的面积为( )A、cm2 B、cm2 C、cm2 D、cm2二、填空题
-
11. 如图,是矩形的外接圆,若 , 则图中阴影部分的面积为 . (结果保留)
 12. 拓展课上,同学们准备用卡纸做一个底面为边长为的正六边形,高为的无盖包装盒,它的表面展开图如图1所示.
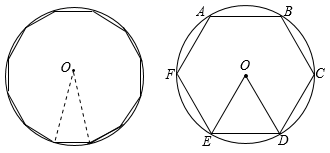
12. 拓展课上,同学们准备用卡纸做一个底面为边长为的正六边形,高为的无盖包装盒,它的表面展开图如图1所示.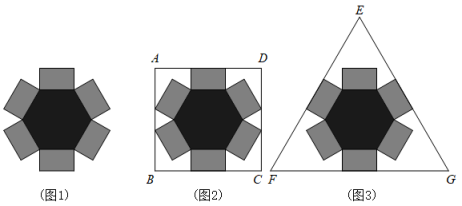 (1)、若选用长方形卡纸按图2方式剪出包装盒的表面展开图,则的长为;(2)、若选用一块等边三角形卡纸按图3方式剪出包装盒表面展开图,则这个等边三角形的边长为.13. 正六边形内接于圆,则它的边所对的圆周角的度数为.14. 正方形的中心角为 .15. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形来确定圆周率.若设⊙O的半径为R , 圆内接正n边形的边长、面积分别为an , Sn , 圆内接正2n边形边长、面积分别为a2n , S2n . 刘徽用以下公式求出a2n和S2n . , .如图,若⊙O的半径为1,则⊙O的内接正八边形AEBFCGDH的面积为 .
(1)、若选用长方形卡纸按图2方式剪出包装盒的表面展开图,则的长为;(2)、若选用一块等边三角形卡纸按图3方式剪出包装盒表面展开图,则这个等边三角形的边长为.13. 正六边形内接于圆,则它的边所对的圆周角的度数为.14. 正方形的中心角为 .15. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形来确定圆周率.若设⊙O的半径为R , 圆内接正n边形的边长、面积分别为an , Sn , 圆内接正2n边形边长、面积分别为a2n , S2n . 刘徽用以下公式求出a2n和S2n . , .如图,若⊙O的半径为1,则⊙O的内接正八边形AEBFCGDH的面积为 .
三、解答题
-
16. 已知圆内接正十二边形的面积为S,求同圆的内接正六边形的面积.
 17. 如图,已知正三角形ABC内接于 ,AD是 的内接正十二边形的一条边长,连接CD,若 ,求 的半径.
17. 如图,已知正三角形ABC内接于 ,AD是 的内接正十二边形的一条边长,连接CD,若 ,求 的半径.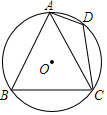 18. 如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
18. 如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):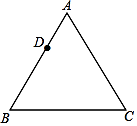 (1)、作△ABC的外心O;(2)、设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F,点H分别在边BC和AC上.19. 如图,已知正n边形边长为a,边心距为r,求正n边形的半径R、周长P和面积S.
(1)、作△ABC的外心O;(2)、设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F,点H分别在边BC和AC上.19. 如图,已知正n边形边长为a,边心距为r,求正n边形的半径R、周长P和面积S.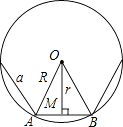
四、综合题
-
20. 如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON
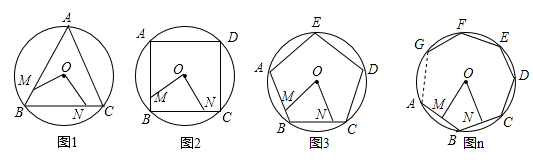 (1)、求图1中∠MON的度数(2)、图2中∠MON的度数是 , 图3中∠MON的度数是(3)、试探究∠MON的度数与正n边形边数n的关系是21. 如图,正方形ABCD内接于⊙O,E是 的中点,连接AE,DE,CE.
(1)、求图1中∠MON的度数(2)、图2中∠MON的度数是 , 图3中∠MON的度数是(3)、试探究∠MON的度数与正n边形边数n的关系是21. 如图,正方形ABCD内接于⊙O,E是 的中点,连接AE,DE,CE. (1)、求证:AE=DE;(2)、若CE=1,求四边形AECD的面积.22. 已知某种月饼形状的俯视图如图1所示,该形状由1个正六边形和6个半圆组成,半圆直径与正六边形的边长相等.
(1)、求证:AE=DE;(2)、若CE=1,求四边形AECD的面积.22. 已知某种月饼形状的俯视图如图1所示,该形状由1个正六边形和6个半圆组成,半圆直径与正六边形的边长相等.
现商家设计了2种棱柱体包装盒,其底面分别为矩形和正六边形(如图2和图3)我们可从底面的利用率来记算整个包装盒的利用情况.(底面利用率= ×100%)
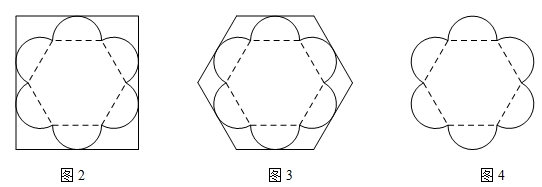 (1)、请分别计算出图2与图3中的底面利用率(结果保留到0.1%);(2)、考虑到节约成本,商家希望底面利用率能够不低于80%,且底面图形仍然采用最基本的几何形状,请问商家的要求是否能够满足,若可以满足,请设计一种方案,并直接写出此时的利用率;若不能满足,请说明理由.
(1)、请分别计算出图2与图3中的底面利用率(结果保留到0.1%);(2)、考虑到节约成本,商家希望底面利用率能够不低于80%,且底面图形仍然采用最基本的几何形状,请问商家的要求是否能够满足,若可以满足,请设计一种方案,并直接写出此时的利用率;若不能满足,请说明理由.