2023年苏科版数学九年级上学期期末复习——圆周角
试卷更新日期:2023-08-03 类型:复习试卷
一、选择题
-
1. 下列命题是假命题的是( )A、两条平行线间的距离处处相等 B、平分弦的直径垂直于弦 C、正方形的两条对角线互相垂直平分 D、在同圆或等圆中,同弧或等弧所对的圆周角相等2. 如图,一块直角三角板的斜边与量角器的直径重合,点D对应的刻度值为 , 则的度数为( )
 A、 B、 C、 D、3. 下列说法正确的是( )A、两点之间,直线最短 B、线段垂直平分线上的点到这条线段两个端点的距离相等 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、圆周角的度数等于圆心角度数的一半4. 如图,点A、B、C是上的三点, , 则的度数是( )
A、 B、 C、 D、3. 下列说法正确的是( )A、两点之间,直线最短 B、线段垂直平分线上的点到这条线段两个端点的距离相等 C、一组对边平行,另一组对边相等的四边形是平行四边形 D、圆周角的度数等于圆心角度数的一半4. 如图,点A、B、C是上的三点, , 则的度数是( )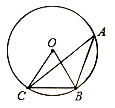 A、 B、 C、 D、5. 如图,在中,直径与弦相交于点P,连接 , 若 , , 则( )
A、 B、 C、 D、5. 如图,在中,直径与弦相交于点P,连接 , 若 , , 则( ) A、 B、 C、 D、6. 如图,A,B,C为上的三个点, , 若 , 则的度数是( )
A、 B、 C、 D、6. 如图,A,B,C为上的三个点, , 若 , 则的度数是( )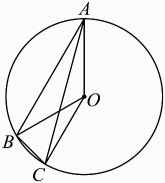 A、 B、 C、 D、12°7. 我国古代天文学确定方向的方法中蕴藏了平行线的作图法.如《淮南子天文训》中记载:“正朝夕:先树一表东方;操一表却去前表十步,以参望日始出北廉.日直入,又树一表于东方,因西方之表,以参望日方入北康.则定东方两表之中与西方之表,则东西也.”如图,用几何语言叙述作图方法:已知直线a和直线外一定点O,过点O作直线与a平行.(1)以O为圆心,单位长为半径作圆,交直线a于点M,N;(2)分别在的延长线及上取点A,B,使;(3)连接 , 取其中点C,过O,C两点确定直线b,则直线 . 按以上作图顺序,若 , 则( )
A、 B、 C、 D、12°7. 我国古代天文学确定方向的方法中蕴藏了平行线的作图法.如《淮南子天文训》中记载:“正朝夕:先树一表东方;操一表却去前表十步,以参望日始出北廉.日直入,又树一表于东方,因西方之表,以参望日方入北康.则定东方两表之中与西方之表,则东西也.”如图,用几何语言叙述作图方法:已知直线a和直线外一定点O,过点O作直线与a平行.(1)以O为圆心,单位长为半径作圆,交直线a于点M,N;(2)分别在的延长线及上取点A,B,使;(3)连接 , 取其中点C,过O,C两点确定直线b,则直线 . 按以上作图顺序,若 , 则( ) A、 B、 C、 D、8. 如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
A、 B、 C、 D、8. 如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )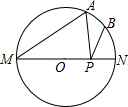 A、4 B、4 C、2 D、29. 如图,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中,不正确的是( )
A、4 B、4 C、2 D、29. 如图,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中,不正确的是( )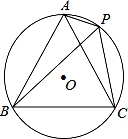 A、当弦PB最长时,△APC是等腰三角形 B、当△APC是等腰三角形时,PO⊥AC C、当PO⊥AC时,∠ACP=30° D、当∠ACP=30°时,△BPC是直角三角形10. 如图,已知平面直角坐标系中,点A,B坐标分别为A(4,0),B(﹣6,0).点C是y轴正半轴上的一点,且满足∠ACB=45°,圆圆得到了以下4个结论:①△ABC的外接圆的圆心在OC上;②∠ABC=60°;③△ABC的外接圆的半径等于5 ;④OC=12.其中正确的是( )
A、当弦PB最长时,△APC是等腰三角形 B、当△APC是等腰三角形时,PO⊥AC C、当PO⊥AC时,∠ACP=30° D、当∠ACP=30°时,△BPC是直角三角形10. 如图,已知平面直角坐标系中,点A,B坐标分别为A(4,0),B(﹣6,0).点C是y轴正半轴上的一点,且满足∠ACB=45°,圆圆得到了以下4个结论:①△ABC的外接圆的圆心在OC上;②∠ABC=60°;③△ABC的外接圆的半径等于5 ;④OC=12.其中正确的是( ) A、①② B、②③ C、③④ D、①④
A、①② B、②③ C、③④ D、①④二、填空题
-
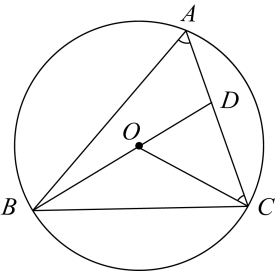
11. 如图所示,点A、B、C是上不同的三点,点O在的内部,连接、 , 并延长线段交线段于点D.若 , 则度.
 12. 如图,内接于 , 外角的平分线交于点 , 射线交延长线于点.若 , , 则的度数为°.
12. 如图,内接于 , 外角的平分线交于点 , 射线交延长线于点.若 , , 则的度数为°.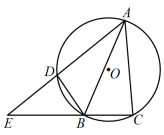 13. 如图,AB是半圆的直径,C为半圆上一点,BC,D为弧BC上一点.连接OD,连接AE,若四边形ACDE为平行四边形,AE=2 , 则AB的长为.
13. 如图,AB是半圆的直径,C为半圆上一点,BC,D为弧BC上一点.连接OD,连接AE,若四边形ACDE为平行四边形,AE=2 , 则AB的长为. 14. 如图,正方形ABCD的边长是4,F点是BC边的中点,点H是CD边上的一个动点,以CH为直径作 ,连接HF交 于E点,连接DE,则线段DE的最小值为.
14. 如图,正方形ABCD的边长是4,F点是BC边的中点,点H是CD边上的一个动点,以CH为直径作 ,连接HF交 于E点,连接DE,则线段DE的最小值为. 15. 如图,已知正方形ABCD的边长为4,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点F是AB边上一动点,连接FD,FE,则FD+FE的长度最小值为.
15. 如图,已知正方形ABCD的边长为4,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点F是AB边上一动点,连接FD,FE,则FD+FE的长度最小值为.
三、作图题
-
16. 如图是由小正方形组成的网格,每个小正方形的顶点叫作格点已知的圆心在格点上,圆上 , 两点均在格线上,仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
 (1)、在图1中,点在圆上,请在直径下方的圆上画出点 , 使;并在网格中找点 , 使为等腰直角三角形,且 .(2)、在图2中,为格点,在直径下方的圆上画出点 , 使得;并在线段上画出点 , 使得 .
(1)、在图1中,点在圆上,请在直径下方的圆上画出点 , 使;并在网格中找点 , 使为等腰直角三角形,且 .(2)、在图2中,为格点,在直径下方的圆上画出点 , 使得;并在线段上画出点 , 使得 .四、解答题
-
17. 如图,在中,平分平分的延长线交的外接圆于点D,连接 . 求证: .
 18. 如图,AB是⊙O的直径,点C在⊙O上,延长BC至点D,使CD=BC,连接DA并延长,与⊙O的另一个交点为E,连接AC,CE.若∠E=26°,求∠D的度数.
18. 如图,AB是⊙O的直径,点C在⊙O上,延长BC至点D,使CD=BC,连接DA并延长,与⊙O的另一个交点为E,连接AC,CE.若∠E=26°,求∠D的度数. 19. 如图所示,圆O为△ABC的外接圆,AM,AT分别为中线和角平分线,过点B和点C的圆O的切线相交于点P,连结AP,与BC和圆O分别相交于点D、E.
19. 如图所示,圆O为△ABC的外接圆,AM,AT分别为中线和角平分线,过点B和点C的圆O的切线相交于点P,连结AP,与BC和圆O分别相交于点D、E.
求证:点T是△AME的内心。
五、综合题
-
20. 如图,已知是等边三角形的外接圆,连接并延长交于点 , 交于点 , 连接 , .
 (1)、写出图中一个度数为的角: , 图中与全等的三角形是;(2)、求证:;(3)、连接 , , 判断四边形的形状,并说明理由.21. 在正方形ABCD中,E、F为平面上两点.
(1)、写出图中一个度数为的角: , 图中与全等的三角形是;(2)、求证:;(3)、连接 , , 判断四边形的形状,并说明理由.21. 在正方形ABCD中,E、F为平面上两点. (1)、【基础巩固】
(1)、【基础巩固】如图1,当点E在边AB上时,DE⊥DF,且B,C,F三点共线,求证:AE=CF;
(2)、【类比应用】如图2,当点E在正方形ABCD外部时,DE⊥DF,AE⊥EF,且E、C、F三点共线,若AE=2,CE=4,求点D到直线EF的距离;
(3)、【拓展迁移】如图3,当点E在正方形ABCD外部时,AE⊥EC,AE⊥AF,DE⊥BE,且D,F,E三点共线,DE与AB交于G点,若DF=3,AE=2 , 求正方形ABCD的边长.
-