2023-2024学年苏科版数学九年级上册2.2圆的对称性 同步练习
试卷更新日期:2023-08-03 类型:同步测试
一、选择题
-
1. 陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一图是从正面看到的一个“老碗”图的形状示意图.是的一部分,是的中点,连接 , 与弦交于点 , 连接 , 已知 , 碗深 , 则的半径为( )
 A、 B、 C、 D、2. 如图,BD是的直径,弦AC交BD于点G.连接OC,若 , , 则的度数为( )
A、 B、 C、 D、2. 如图,BD是的直径,弦AC交BD于点G.连接OC,若 , , 则的度数为( ) A、98° B、103° C、108° D、113°3. 如图,是的直径,弦于点 , , , 则( )
A、98° B、103° C、108° D、113°3. 如图,是的直径,弦于点 , , , 则( ) A、5 B、4 C、3 D、24. 如图,是的外接圆,交于点E,垂足为点D, , 的延长线交于点F.若 , , 则的长是( )
A、5 B、4 C、3 D、24. 如图,是的外接圆,交于点E,垂足为点D, , 的延长线交于点F.若 , , 则的长是( ) A、8 B、12 C、16 D、205. 如图为一座拱形桥示意图,桥身(弦)长度为8,半径垂直于点 , , 则桥拱高为( )
A、8 B、12 C、16 D、205. 如图为一座拱形桥示意图,桥身(弦)长度为8,半径垂直于点 , , 则桥拱高为( ) A、3 B、2.5 C、2 D、1.56. 下列命题正确的是( )A、相等的圆心角所对的两条弦相等 B、圆既是中心对称图形又是轴对称图形 C、两个圆中,如果弦相等,则弦所对的圆心角也相等 D、等弧就是长度相等的弧7. “圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长六寸,问径几何?”用现代的数学语言表述是:“为的直径,弦 , 垂足为E,寸,寸,求直径的长?”依题意得的长为( )
A、3 B、2.5 C、2 D、1.56. 下列命题正确的是( )A、相等的圆心角所对的两条弦相等 B、圆既是中心对称图形又是轴对称图形 C、两个圆中,如果弦相等,则弦所对的圆心角也相等 D、等弧就是长度相等的弧7. “圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长六寸,问径几何?”用现代的数学语言表述是:“为的直径,弦 , 垂足为E,寸,寸,求直径的长?”依题意得的长为( ) A、4寸 B、5寸 C、8寸 D、10寸8. 点是内一点,过点的最长弦的长为10,最短弦的长为6,则的长为( )A、8 B、2 C、5 D、49. 如图,AB为⊙O的直径,点C为⊙O上一点,连接CO,作AD OC,若CO= ,AC=2,则AD=( )
A、4寸 B、5寸 C、8寸 D、10寸8. 点是内一点,过点的最长弦的长为10,最短弦的长为6,则的长为( )A、8 B、2 C、5 D、49. 如图,AB为⊙O的直径,点C为⊙O上一点,连接CO,作AD OC,若CO= ,AC=2,则AD=( )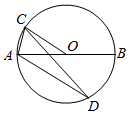 A、3 B、 C、 D、10. 如图,点A、B、C是圆O上的三点,且四边形OABC是平行四边形,OD⊥AB交圆O于点D,则∠OAD等于( )
A、3 B、 C、 D、10. 如图,点A、B、C是圆O上的三点,且四边形OABC是平行四边形,OD⊥AB交圆O于点D,则∠OAD等于( ) A、72.5° B、75° C、80° D、60°
A、72.5° B、75° C、80° D、60°二、填空题
-
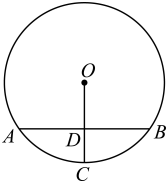
11. ⊙O的半径为13cm,弦ABCD,AB=10cm, CD=24cm,则AB与CD之间的距离是.12. 如图,是的弦,C是弧AB的中点,交于点D.若cm, cm,则的半径为 cm.
 13. 已知如图,是等边三角形,分别以点A、B、C为圆心,长为半径作圆,得到弧、弧、弧 , , D为弧上任一点,连接 , 则= .
13. 已知如图,是等边三角形,分别以点A、B、C为圆心,长为半径作圆,得到弧、弧、弧 , , D为弧上任一点,连接 , 则= . 14. 的半径是13cm,AB,CD是的两条弦,且 , , , 则AB与CD之间的距离是 .15. 在如图所示的网格中,每个小正方形的边长都为1,是的外接圆,点 , 均为格点,点是小正方形一边的中点.
14. 的半径是13cm,AB,CD是的两条弦,且 , , , 则AB与CD之间的距离是 .15. 在如图所示的网格中,每个小正方形的边长都为1,是的外接圆,点 , 均为格点,点是小正方形一边的中点. (1)、线段的长度等于;(2)、请借助无刻度的直尺,在给定的网格中先确定圆心 , 再作的平分线交于点 . 在下面的横线上简要说明点和点的位置是如何找到的. .16. 如图1,一艺术拱门由两部分组成,下部为矩形ABCD,AB,AD的长分别是2 m和4m,上部是圆心为O的劣弧CD,圆心角∠COD=120°.现欲以B点为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2、图3、图4所示记拱门上的点到地面的最大距离hm,则h的最大值为m.
(1)、线段的长度等于;(2)、请借助无刻度的直尺,在给定的网格中先确定圆心 , 再作的平分线交于点 . 在下面的横线上简要说明点和点的位置是如何找到的. .16. 如图1,一艺术拱门由两部分组成,下部为矩形ABCD,AB,AD的长分别是2 m和4m,上部是圆心为O的劣弧CD,圆心角∠COD=120°.现欲以B点为支点将拱门放倒,放倒过程中矩形ABCD所在的平面始终与地面垂直,如图2、图3、图4所示记拱门上的点到地面的最大距离hm,则h的最大值为m.
三、作图题
-
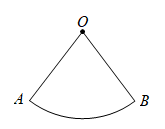
17. 如图,已知扇形 , 请用尺规作图,在上求作一点P,使(保留作图痕迹,不写作法).
四、综合题



