2023-2024学年北师大版数学八年级上册2.7二次根式（培优卷）

试卷更新日期：2023-08-03 类型：同步测试

进入出卷网下载

一、选择题

1. 已知实数a满足条件 $| 2011 - a | + \sqrt{a - 2012} = a$ ，那么 $a - 2011^{2}$ 的值为 $($ 　　 $)$

A、2010 B、2011 C、2012 D、2013

查看试题解析
2. “分母有理化”是我们常用的一种化简的方法，如： $\frac{2 + \sqrt{3}}{2 - \sqrt{3}} = \frac{(2 + \sqrt{3}) (2 + \sqrt{3})}{(2 - \sqrt{3}) (2 + \sqrt{3})} = 7 + 4 \sqrt{3}$ ，除此之外，我们也可以用平方之后再开方的方式来化简一些有特点的无理数，如：对于 $\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}}$ ，设x= $\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}}$ ，易知 $\sqrt{3 + \sqrt{5}}$ > $\sqrt{3 - \sqrt{5}}$ ，故x>0，由x²= ${(\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}})}^{2}$ = $3 + \sqrt{5} + 3 - \sqrt{5} - 2 \sqrt{(3 + \sqrt{5}) (3 - \sqrt{5})}$ =2，解得x= $\sqrt{2}$ ，即 $\sqrt{3 + \sqrt{5}} - \sqrt{3 - \sqrt{5}} = \sqrt{2}$ 。根据以上方法，化简 $\frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} + \sqrt{2}} + \sqrt{6 - 3 \sqrt{3}} - \sqrt{6 + 3 \sqrt{3}}$ 后的结果为（）

A、5+3 $\sqrt{6}$ B、5+ $\sqrt{6}$ C、5- $\sqrt{6}$ D、5-3 $\sqrt{6}$

查看试题解析
3. 下列各实数中最大的一个是（）

A、5× $\sqrt{0.039}$ B、 $\frac{3.141}{π}$ C、 $\frac{7}{\sqrt{14} + \sqrt{7}}$ D、 $\sqrt{0.3}$ + $\sqrt{0.2}$

查看试题解析
4. 用四张一样大小的长方形纸片拼成一个如图所示的正方形 $A B C D$ ，它的面积是75， $A E = 3 \sqrt{3}$ ，图中空白的地方是一个正方形，那么这个小正方形的周长为（）

A、 $2 \sqrt{3}$ B、 $4 \sqrt{3}$ C、 $5 \sqrt{3}$ D、 $6 \sqrt{3}$

查看试题解析
5. 如图．从一个大正方形中裁去面积为8m²和18cm²的两个小正方形，则留下的阴影部分的面积为（）

A、 $5 \sqrt{2}$ cm² B、 $12$ cm² C、 $8$ cm² D、 $24$ cm²

查看试题解析
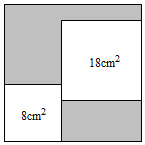6. 已知a是1997的算术平方根的整数部分，b是1991的算术平方根的小数部分，则化简 $\frac{\sqrt{a}}{(\sqrt{181} + 4 \sqrt{11}) b}$ 的结果为（）

A、 $\frac{1}{5}$ B、 $\frac{1}{4}$ C、 $\frac{2}{5}$ D、 $\frac{2}{11}$

查看试题解析
7. 下列计算中，正确的是（）

A、 $(3 + 2 \sqrt{3}) (3 - 2 \sqrt{3}) = - 3$ B、 $（ \sqrt{2} + \sqrt{3} ） \sqrt{5} = 5$ C、 $2 \sqrt{3} + 3 \sqrt{2} = 5 \sqrt{5}$ D、 $(\sqrt{2 a} + \sqrt{b}) (\sqrt{2 a} + \sqrt{b}) = 2 a - b$

查看试题解析
8. 计算： $(3 \sqrt{48} - 2 \sqrt{27}) \div \sqrt{3} =$ （）

A、4 B、5 C、6 D、8

查看试题解析
9. 已知m＝ $\sqrt{8} \times \sqrt{\frac{1}{2}} + \sqrt{3}$ ，则以下对m的值估算正确的（）

A、2＜m＜3 B、3＜m＜4 C、4＜m＜5 D、5＜m＜6

查看试题解析
10. 下列计算中，正确的是（）

A、 $2 \sqrt{3} + 3 \sqrt{2} = 5 \sqrt{5}$ B、 $(\sqrt{3} + \sqrt{7}) • \sqrt{10} = \sqrt{10} • \sqrt{10} = 1$ C、 $(3 + 2 \sqrt{3}) (3 - 2 \sqrt{3}) = - 3$ D、 $(\sqrt{2 a} + \sqrt{b}) (\sqrt{2 a} - \sqrt{b}) = 2 a + b$

查看试题解析

二、填空题

11. 完成下列各题，

(1)、若 $\frac{3}{a} = \frac{4}{b}$ ，那么 $\sqrt{\frac{2 a + b}{b}}$ 的值是．

(2)、化简： $\sqrt{22 - 6 \sqrt{13}} =$ ．

查看试题解析
12. 已知a、b是正整数，如果有序数对(a, b)能使得2 $(\sqrt{\frac{1}{a}} + \sqrt{\frac{1}{b}})$ 的值也是整数，那么称（a,b）是2 $(\sqrt{\frac{1}{a}} + \sqrt{\frac{1}{b}})$ 的一个“理想数对”。如（1，1）使得2 $(\sqrt{\frac{1}{a}} + \sqrt{\frac{1}{b}})$ =4，（4，4）使得2 $(\sqrt{\frac{1}{a}} + \sqrt{\frac{1}{b}})$ 所以（1,1）和（4，4）都是2 $(\sqrt{\frac{1}{a}} + \sqrt{\frac{1}{b}})$ 的“理想数对”，请你再写出一个2 $(\sqrt{\frac{1}{a}} + \sqrt{\frac{1}{b}})$ 的“理想数对”： .

查看试题解析
13. 计算： $2 \sqrt{3} \times (- \sqrt{6}) =$ .

查看试题解析
14. 如图，在长方形 $A B C D$ 内，两个小正方形的面积分别为 $2$ ， $18$ ，则图中阴影部分的面积等于.

查看试题解析
15. 已知长方形的长和宽分别为 $\sqrt{8}$ ， $\sqrt{2}$ ，则它的周长=.

查看试题解析

三、综合题

16. 小明在解决问题：已知 $a = \frac{1}{2 + \sqrt{3}}$ ，求 $2 a^{2} - 8 a + 1$ 的值，他是这样分析与解答的：
$∵ a = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ，
$∴ a = 2 - \sqrt{3}$ ，
$∴ a - 2 = - \sqrt{3}$ ，
$∴ (a - 2)^{2} = 3$ ，
$∴ a^{2} - 4 a + 4 = 3$ ， $∴ a^{2} - 4 a = - 1$ ，
$∴ 2 a^{2} - 8 a + 1 = 2 (a^{2} - 4 a) + 1 = 2 \times (- 1) + 1 = - 1$ ．
请你认真审视小明的解答过程，根据他的做法解决下列问题：

(1)、计算 $\frac{1}{\sqrt{n + 1} + \sqrt{n}} =$ ；

(2)、计算 $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots + \frac{1}{\sqrt{2020} + \sqrt{2019}}$ （写出计算过程）；

(3)、如果 $a = \frac{1}{\sqrt{5} - 2}$ ，求 $2 a^{2} - 8 a + 1$ 的值．

查看试题解析
17. 已知 $x = \frac{2}{\sqrt{3} + 1}$ ， $y = \frac{2}{\sqrt{3} - 1}$ ．

(1)、对x，y进行化简；

(2)、求 $x^{2} + x y + y^{2}$ 的值．

查看试题解析
18. 阅读材料：像 $(\sqrt{5} + \sqrt{2}) (\sqrt{5} - \sqrt{2}) = 3$ 、 $\sqrt{a} \cdot \sqrt{a} = a$ $(a \geq 0)$ 、 $(\sqrt{b} + 1) (\sqrt{b} - 1) = b - 1 (b \geq 0) \dots \dots$ 两个含有二次根式的代数式相乘，积不含有二次根式，我们称这两个代数式互为有理化因式 $.$ 例如， $\sqrt{3}$ 与 $\sqrt{3}$ 、 $\sqrt{2} + 1$ 与 $\sqrt{2} - 1$ 、 $2 \sqrt{3} + 3 \sqrt{5}$ 与 $2 \sqrt{3} - 3 \sqrt{5}$ 等都是互为有理化因式 $.$ 在进行二次根式计算时，利用有理化因式，可以化去分母中的根号．
例如； $\frac{1}{2 \sqrt{3}} = \frac{\sqrt{3}}{2 \sqrt{3} \times \sqrt{3}} = \frac{\sqrt{3}}{6}$ ； $\frac{\sqrt{2} + 1}{\sqrt{2} - 1} = \frac{{(\sqrt{2} + 1)}^{2}}{(\sqrt{2} - 1) (\sqrt{2} + 1)} = 3 + 2 \sqrt{2}$ ．
解答下列问题：

(1)、 $3 - \sqrt{7}$ 与互为有理化因式，将 $\frac{2}{3 \sqrt{2}}$ 分母有理化得；

(2)、计算： $\frac{1}{2 - \sqrt{3}} - \frac{6}{\sqrt{3}}$ ；

(3)、已知有理数a、b满足 $\frac{a}{\sqrt{2} + 1} + \frac{b}{\sqrt{2}} = - 1 + 2 \sqrt{2}$ ，求a、b的值．

查看试题解析
19. 大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部写出来，因为 $1 < \sqrt{2} < 2$ ，所以可用、 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分.请解答下列问题：

(1)、 $\sqrt{10}$ 的整数部分是，小数部分是.

(2)、如果 $\sqrt{3} + 3$ 的整数部分为a，小数部分为b，求 $a - b - 1$ 的值.

(3)、已知 $9 - \sqrt{3} = x + y$ ，其中x是整数，且 $0 < y < 1$ .则求 $x + \sqrt{3} + y$ 的平方根的值.

查看试题解析
20. 三角形的周长为 $(5 \sqrt{5} + 2 \sqrt{10}) cm$ ，面积为 $(20 \sqrt{6} + 4 \sqrt{5}) {cm}^{2}$ ，已知两边的长分别为 $\sqrt{45} cm$ 和 $\sqrt{40} cm$ ，求：

(1)、第三边的长；

(2)、第三边上的高．

查看试题解析