2023-2024学年北师大版数学八年级上册2.6实数 同步练习(培优卷)
试卷更新日期:2023-08-03 类型:同步测试
一、选择题
-
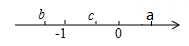
1. 实数a , b , c , d在数轴上的对应点的位置如图所示.若 ,则下列结论中正确的是( )
 A、 B、 C、 D、2. 在实数范围内定义运算“♀”,该运算同时满足下列条件:(1)x♀x=5,(x≠5);(2)x♀(y♀z)=(x♀y)+z,则2015♀2017的值是( )A、2 B、3 C、2015 D、20173. 若6- 的整数部分为x,小数部分为y,则(2x+ )y的值是( )A、5-3 B、3 C、3 -5 D、-34. 如图,数轴上 , , , 四点中,与对应的点距离最近的是( )
A、 B、 C、 D、2. 在实数范围内定义运算“♀”,该运算同时满足下列条件:(1)x♀x=5,(x≠5);(2)x♀(y♀z)=(x♀y)+z,则2015♀2017的值是( )A、2 B、3 C、2015 D、20173. 若6- 的整数部分为x,小数部分为y,则(2x+ )y的值是( )A、5-3 B、3 C、3 -5 D、-34. 如图,数轴上 , , , 四点中,与对应的点距离最近的是( ) A、点 B、点 C、点 D、点5. 如图所示,在数轴上点A所表示的数为a,CD=1,则a的值为( )
A、点 B、点 C、点 D、点5. 如图所示,在数轴上点A所表示的数为a,CD=1,则a的值为( )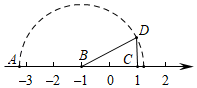 A、 B、-1 C、1 D、-16. 如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连结OC,以O为圆心,OC长为半径画弧交数轴于点M,则点M对应的实数为( )
A、 B、-1 C、1 D、-16. 如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰△ABC,连结OC,以O为圆心,OC长为半径画弧交数轴于点M,则点M对应的实数为( )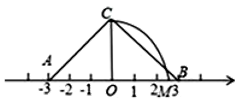 A、 B、4 C、 D、2.57. 如果、分别是的整数部分和小数部分,则( )A、 B、 C、 D、8. 如图,矩形中,在数轴上,若以点A为圆心,对角线的长为半径作到交数轴的正半轴于M,则点M,在数轴上表示的数为( )
A、 B、4 C、 D、2.57. 如果、分别是的整数部分和小数部分,则( )A、 B、 C、 D、8. 如图,矩形中,在数轴上,若以点A为圆心,对角线的长为半径作到交数轴的正半轴于M,则点M,在数轴上表示的数为( )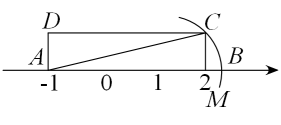 A、2 B、 C、 D、9. 如图,在数轴上表示实数+1的点可能是( )
A、2 B、 C、 D、9. 如图,在数轴上表示实数+1的点可能是( )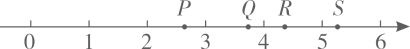 A、P B、Q C、R D、S10. 计算: =( )A、 B、0 C、-1 D、
A、P B、Q C、R D、S10. 计算: =( )A、 B、0 C、-1 D、二、填空题
-
11. 已知实数a、b、c在数轴上的位置如图所示,化简代数式|a|-+-的结果等于.
 12. .13. 如图,Rt△MBC中,∠MCB=90°,点M在数轴﹣1处,点C在数轴1处,MA=MB,BC=1,则数轴上点A对应的数是 .
12. .13. 如图,Rt△MBC中,∠MCB=90°,点M在数轴﹣1处,点C在数轴1处,MA=MB,BC=1,则数轴上点A对应的数是 . 14. 若 , 则 .15. 计算:(-8)2019×0.1252018+(-3.14)0-( )-1的结果为。
14. 若 , 则 .15. 计算:(-8)2019×0.1252018+(-3.14)0-( )-1的结果为。三、解答题
-
16. 把下列各数按要求填入相应的大括号里:
4.5, , 0, , 2.10010001……, , , -10,整数集合:{ … },
分数集合:{ … },
正有理数集合:{ … },
无理数集合:{ … }.
17. 甲同学用如图所示的方法作出C点表示数 , 在中, , , , 且点O,A,C在同一数轴上, .仿照甲同学的做法,在如图所示的数轴上描出表示的点F.

 18. 如图1,数轴上,O点与C点对应的数分别是0、60(单位:单位长度),将一根质地均匀的直尺AB放在数轴上(A在B的左边),若将直尺在数轴上水平移动,当A点移动到B点的位置时,B点与C点重合,当B点移动到A点的位置时,A点与O点重合.
18. 如图1,数轴上,O点与C点对应的数分别是0、60(单位:单位长度),将一根质地均匀的直尺AB放在数轴上(A在B的左边),若将直尺在数轴上水平移动,当A点移动到B点的位置时,B点与C点重合,当B点移动到A点的位置时,A点与O点重合. (1)、直尺的长为个单位长度(直接写答案)(2)、如图2,直尺AB在数轴上移动,有BC=3OA,求此时A点对应的数;
(1)、直尺的长为个单位长度(直接写答案)(2)、如图2,直尺AB在数轴上移动,有BC=3OA,求此时A点对应的数;
(3)、如图3,以OC为边搭一个横截面为长方形的不透明的篷子,将直尺放入篷内的数轴上的某处(看不到直尺的任何部分,A在B的左边),将直尺AB沿数轴以5个单位/秒的速度分别向左、向右移动,直到完全看到直尺,所经历的时间为t1、t2 , 若t1﹣t2=2(秒),求直尺放入蓬内,A点对应的数为多少?19. 如图,数轴上有A.B两点,AB=12,原点O是线段AB上的一点,OA=2OB. (1)、写出A,B两点所表示的实数;(2)、若点C是线段AB上一点,且满足AC=CO+CB,求C点所表示的实数;(3)、若动点P、Q分别从A.B同时出发,向右运动,点P的速度为每秒2个单位长度,点Q的速度为每秒1个单位长度,设运动时间为t秒,当点P与点Q重合时,P、Q两点停止运动.
(1)、写出A,B两点所表示的实数;(2)、若点C是线段AB上一点,且满足AC=CO+CB,求C点所表示的实数;(3)、若动点P、Q分别从A.B同时出发,向右运动,点P的速度为每秒2个单位长度,点Q的速度为每秒1个单位长度,设运动时间为t秒,当点P与点Q重合时,P、Q两点停止运动.①当t为何值时,2OP﹣OQ=4;
②当点P到达点O时,动点M从点O出发,以每秒3个单位长的速度也向右运动,当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后再立即返回,以同样的速度向点Q运动,如此往返,直到点P、Q停止时,点M也停止运动,求在此过程中,点M行驶的总路程和点M最后位置在数轴上对应的实数.
20. 阅读下列材料:“为什么不是有理数”.假是有理数,那么存在两个互质的正整数m,n,使得= , 于是有2m2=n2 .
∵2m2是偶数,∴n2也是偶数,∴n是偶数.
设n=2t(t是正整数),则n2=2m,∴m也是偶数
∴m,n都是偶数,不互质,与假设矛盾.
∴假设错误
∵不是有理数
有类似的方法,请证明不是有理数.