2023-2024学年北师大版数学八年级上学期微专题复习—— 无理数（提升卷）

试卷更新日期：2023-08-03 类型：复习试卷

进入出卷网下载

一、选择题

1. 在-1.414， $\sqrt{2}$ ， π，2+ $\sqrt{3}$ ， 3.212212221…，3.14这些数中，无理数的个数为（）

A、5 B、2 C、3 D、4

查看试题解析
2. 在下列实数 $\sqrt{3}$ ， 0.31， $\frac{π}{3}$ ， $- \frac{2}{7}$ ， $\sqrt{9}$ ， $| - \frac{1}{2} |$ ， $\sqrt[3]{8}$ ， 1.212 212 221 …（每两个1之间依次多一个2)中，无理数的个数为（ )

A、4 B、3 C、2 D、1

查看试题解析
3. 在 0，0.2，3π， $\frac{22}{7}$ ， 6.1010010001…， $\frac{131}{11}$ ， $\sqrt{7}$ 中，无理数有（）个

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列说法错误的是（　　）

A、无理数的相反数还是无理数 B、正无理数、负无理数统称为无理数 C、无限小数都是无理数 D、实数与数轴上的点一一对应

查看试题解析
5. 下列说法正确的有（）
①无限小数不一定是无理数；②无理数一定是无限小数；③带根号的数不一定是无理数；④不带根号的数一定是有理数．

A、①②③ B、②③④ C、①③④ D、①②④

查看试题解析
6. 下列各数中无理数有（）
-1.732， $\sqrt{2}$ ，π， $2 + \sqrt{3}$ ，3.212212221……，3.14， $- \frac{22}{7}$ ， $\sqrt[3]{- 27}$ .

A、4个 B、3个 C、2个 D、5个

查看试题解析
7. 如图，在4×4的正方形网格中，所有线段的端点都在格点处，则这些线段的长度是无理数的有（　　）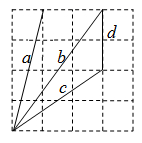

A、1 条 B、2条 C、3条 D、4条

查看试题解析
8. 在实数 $\sqrt{5}$ 、3.1415、π、 $\sqrt{144}$ 、 $\sqrt[3]{6}$ 、2.123122312223……（1和3之间的2逐次加1个）中，无理数的个数为（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
9. 在实数： $\frac{2019}{2020}$ ，π， $\sqrt{9}$ ， $\sqrt{3}$ ，2π， $\sqrt[3]{8}$ ，0.36，0.3737737773…（相邻两个3之间7的个数逐次加1）， $- \frac{5}{2}$ ， $\sqrt{\frac{4}{9}}$ 中，无理数的个数为（）

A、4 B、5 C、6 D、7

查看试题解析
10. 如图为5×5的正方形格子，其中所有线段的端点都在格点上，长度是无理数的线段有（）

A、b、c、d B、c、d C、a、d D、b、c

查看试题解析

二、填空题

11. 六张卡片的正面分别写有 $π$ ， $\frac{1}{3}$ ， $\sqrt{5}$ ， 0， $\sqrt[3]{8}$ ， $- 0.1212212221$ 这六个数，将卡片的正面朝下（反面完全相同）放在桌子上，从中任意抽取一张，卡片上的数字为无理数的可能性大小是．

查看试题解析
12. 请写出一个大于1小于3的无理数．

查看试题解析
13. 在实数： $- \frac{π}{3}$ ， ${(\sqrt{2})}^{0}$ ， $\frac{22}{7}$ ， $\frac{\sqrt{2}}{2}$ ，3.14， $- \sqrt[3]{0.001}$ 中，无理数有个.

查看试题解析
14. 若 $a$ 、 $b$ 都是无理数，且 $a + b = 2$ ，则 $a$ 、 $b$ 的值可以是（填上一组满足条件的值即可）.

查看试题解析
15. 如图，在5×5的正方形网格中，以AB为边画直角△ABC，使点C在格点上，且另外两条边长均为无理数，满足这样条件的点C共个．

查看试题解析

三、综合题

16. 如图，在5×5的正方形网格中，每个小正方形的边长都为1，请在所给网格中解答下面问题．

(1)、图中线段AB的两端点都落在格点（即小正方形的顶点）上，求出AB的长度

(2)、再以AB为一边画一个等腰三角形ABC，使点C在格点上，且另两边的长都是无理数；

(3)、请直接写出符合(2)中条件的等腰三角形ABC的顶点C的个数.

查看试题解析
17. 如果正方形网格中的每一个小正方形的边长都是1，则每个小格的顶点叫做格点.

(1)、如图①，以格点为顶点的 $△ A B C$ 中，请判断AB，BC，AC三边的长度是有理数还是无理数？

(2)、在图②中，以格点为顶点画一个三角形，使三角形的三边长分别为3， $\sqrt{5}$ ， $2 \sqrt{2}$ .

查看试题解析
18. 课堂上，老师让同学们从下列数中找一个无理数：
$- \frac{22}{7}$ ， $- \sqrt{2}$ ， $| - \frac{1}{2} |$ ，0， $2 π$ ， $- \sqrt[3]{8}$ ，

其中，甲说“ $- \frac{22}{7}$ ”，乙说“ $- \sqrt{2}$ ”，丙说“ $2 π$ ”

(1)、甲、乙、丙三个人中，说错的是．

(2)、请将老师所给的数字按要求填入下面相应的区域内；

查看试题解析
19. 如图，是一个数值转换器，原理如图所示．

(1)、当输入的x值为16时，求输出的y值；

(2)、是否存在输入的x值后，始终输不出y值？如果存在，请直接写出所有满足要求的x值；如果不存在，请说明理由．

(3)、输入一个两位数x，恰好经过两次取算术平方根才能输出无理数，则x= ．

查看试题解析
20. 无限循环小数如何化为分数呢？请你仔细阅读下列资料：由于小数部分位数是无限的，所以不可能写成十分之几、百分之几、千分之几等等的数．转化时需要先去掉无限循环小数的“无限小数部分”．一般是用扩倍的方法，把无限循环小数扩大十倍、一百倍或一千倍…使扩大后的无限循环小数与原无限循环小数的“无限小数部分”完全相同，然后这两个数相减，这样“大尾巴”就剪掉了．例题：例如把 $0. \dot{3}$ 和 $0.2 \dot{1} \dot{7}$ 化为分数

请用以上方法解决下列问题

(1)、把 $0. \dot{1} \dot{7}$ 化为分数

(2)、把 $0.3 \dot{1} \dot{3}$ 化为分数．

查看试题解析