2023-2024学年北师大版数学八年级上册1.3勾股定理的应用 同步练习（培优卷）
试卷更新日期：2023-08-03 类型：同步测试
一、选择题
-
1. 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用 、 表示直角三角形的两直角边 ，下列四个说法：① ，② ，③ ，④ ．其中说法正确的是（ ）
A、①③ B、①②③ C、①②④ D、①②③④2. 勾股定理是几何中的一个重要定理，在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的，可用其面积关系验证勾股定理.图2是由图1放入矩形内得到的， ， ， .点D，E，F，G，H，I都在矩形 的边上，则矩形 的面积为（ ）．
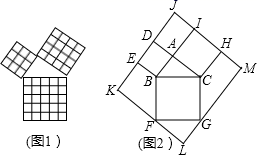A、288 B、400 C、432 D、4403. 一位无线电爱好者把天线杆设在接收效果最佳的矩形屋顶之上．然后，他从杆顶到屋顶四角之间安装固定用的支撑线．有两根相对的支撑线分别长7米和4米，另一根长1米，则最后一根的长度应为（ ）
A、8米 B、9米 C、10米 D、12米4. 如图，将一根长的铅笔放入底面直径为 ， 高为的圆柱形笔筒中，设铅笔露在笔筒外面的长度为 ， 则x的最小值是（ ）
A、5 B、7 C、12 D、135. 如图，已知网格中每个小正方形的边长均为1，以点A为圆心，AB为半径画弧交网格线于点D，则ED的长为（ ）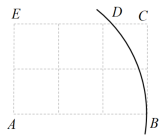
A、 B、3 C、2 D、6. 如图，校园内的一块草坪是长方形 ， 已知 ， ． 从A点到C点，同学们为了抄近路，常沿线段走．这样做会踩坏草坪，而实际上只少走了（ ）
A、 B、 C、 D、7. 如图有一个水池，水面BE的宽为16尺，在水池的中央有一根芦苇，它高出水面2尺，如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面，则这个芦苇的高度是（ ）
A、26尺 B、24尺 C、17尺 D、15尺8. 现有一楼房发生火灾，消防队员决定用消防车上的云梯救人，如图（1）已知云梯最多只能伸长到15m，消防车高3m．救人时云梯伸长至最长，在完成从12m高处救人后，还要从15m高处救人，这时消防车要从原处再向着火的楼房靠近的距离 为（ ）
A、3米 B、5米 C、7米 D、9米9. 如图，学校有一块长方形草地，有极少数人为了避开拐角走“捷径”，在草地内走出了一条“路”，他们仅仅少走了（ ）米路，却紧伤了花草.
A、1 B、2 C、5 D、1210. 如图所示，小明准备测量一段河水的深度，他把一根竹竿竖直插到离岸边1.5m远的水底，竹竿高出水面0.5m，把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，则河水的深度为（ ）
A、2m B、2.25m C、2.5m D、3m二、填空题
-
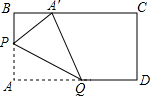
11. 动手操作：在长方形纸片ABCD中，AB＝6，AD＝10．如图所示，折叠纸片，使点A落在BC边上的A′处，折痕为PQ ， 当点A′在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动，则点A′在BC边上可移动的最大距离为 ．
12. 如图，以直角三角形的三边为边向外作三个正方形A、B、C ． 若 ， ，则 ．
13. 已知，如图，在 中， 是 上的中线，如果将 沿 翻折后，点B的对应点 ，那么 的长为 ．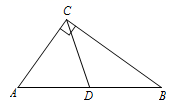
14. 如图是学校艺术馆中的柱子，高4.5m ． 为迎接艺术节的到来，工作人员用一条花带从柱底向柱顶均匀地缠绕3圈，一直缠到起点的正上方为止．若柱子的底面周长是2m ， 则这条花带至少需要m ．
15. 在平面直角坐标系中，已知点 、 ，点 在坐标轴上，且 ，写出满足条件的所有点 的坐标.三、综合题
-
16. 如图所示，在矩形ABCD中，AB=CD=5，BC=AD=3.
(1)、如图①，E、F分别为CD、AB边上的点，将矩形ABCD沿EF翻折，使点A与点C重合，设CE=x ， 则DE=(用含x的代数式表示)，CD′=AD=3，在Rt△CD′E中，利用勾股定理列方程，可求得CE=.(2)、如图②，将△ABD沿BD翻折至△A′BD，若A′B交CD于点E，求此时CE的长；(3)、如图③，P为AD边上的一点，将△ABP沿BP翻折至△A′BP，A′B、A′P分别交CD边于E. F，且DF=A′F，请直接写出此时CE的长.17. 数与形是数学中的两个最古老，也是最基本的研究对象，它们在一定条件下可以互相转化.树形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化，从而起到优化解题途径的目的.(1)、（思想应用）已知m， n均为正实数，且m+n=2求 的最小值通过分析，爱思考的小明想到了利用下面的构造解决此问题：如图，AB=2，AC=1，BD=2，AC⊥AB，BD⊥AB，点E是线段AB上的动点，且不与端点重合，连接CE，DE，设AE=m， BE=n.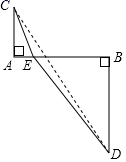
①用含m的代数式表示CE= ， 用含n的代数式表示DE=；
②据此求 的最小值；
(2)、（类比应用）根据上述的方法，求代数式 的最小值.18. 在四边形ABDE中，C是BD边的中点．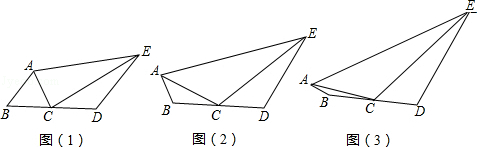
(1)、如图（1），若AC平分∠BAE，∠ACE=90°，则线段AE、AB、DE的长度满足的数量关系为；（直接写出答案）(2)、如图（2），AC平分∠BAE，EC平分∠AED，若∠ACE=120°，则线段AB、BD、DE、AE的长度满足怎样的数量关系？写出结论并证明；(3)、如图（3），BD=8，AB=2，DE=8，若ACE=135°，则线段AE长度的最大值是（直接写出答案）．19. 如图，C为线段BD上一动点，分别过点B，D作AB⊥BD，ED⊥BD，连接AC，EC．已知AB＝5，DE＝1，BD＝8，设CD＝x．
(1)、用含x的代数式表示AC＋CE的长；(2)、请问点C满足什么条件时AC＋CE的值最小？求出最小值．(3)、根据（2）中的结论，请构图求出代数式的最小值．20. 截长补短法，是初中几何题中一种添加辅助线的方法，也是把几何题化难为易的一种策略．截长就是在长边上截取一条线段与某一短边相等，补短就是通过延长或旋转等方式使两条短边拼合到一起，从而解决问题．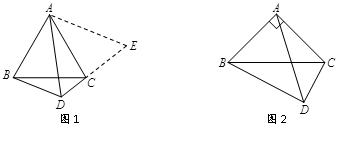
(1)、如图1，△ABC是等边三角形，点D是边BC下方一点，∠BDC＝120°，探索线段DA、DB、DC之间的数量关系．解题思路：延长DC到点E，使CE＝BD，根据∠BAC＋∠BDC＝180°，可证∠ABD＝∠ACE，易证△ABD≌△ACE，得出△ADE是等边三角形，所以AD＝DE，从而解决问题．
根据上述解题思路，三条线段DA、DB、DC之间的等量关系是；（直接写出结果）
(2)、如图2，Rt△ABC中，∠BAC＝90°，AB＝AC．点D是边BC下方一点，∠BDC＝90°，探索三条线段DA、DB、DC之间的等量关系，并证明你的结论．