2023-2024学年北师大版数学八年级上册1.3勾股定理的应用 同步练习（提升卷）
试卷更新日期：2023-08-03 类型：同步测试
一、选择题
-
1. 图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的.若AC＝6，BC＝5，将四个直角三角形中的边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是（ ）
A、51 B、49 C、76 D、无法确定2. 《九章算术》中记录了这样一则“折竹抵地”问题：今有竹高一丈，末折抵地，去本四尺，问折者高几何？意思是：一根竹子，原高一丈，一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部4尺远（如图），则折断后的竹子高度为多少尺？（1丈=10尺）如果我们假设折断后的竹子高度为尺，根据题意，可列方程为（ ）
A、 B、 C、 D、3. 勾股定理是人类早期发现并证明的重要数学定理之一，是用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一．它不但因证明方法层出不穷吸引着人们，更因为应用广泛而使人入迷．如图，秋千静止时，踏板离地的垂直高度 ， 将它往前推至处时（即水平距离），踏板离地的垂直高度 ， 它的绳索始终拉直，则绳索的长是（ ）
A、 B、 C、6 D、4. 数形结合是数学的重要思想和解题方法，如：“当0＜x＜12时，求代数式 的最小值”，其中 可看作两直角边分别为x和2的Rt△ACP的斜边长， 可看作两直角边分别是12-x和3的Rt△BDP的斜边长.于是将问题转化为求AP+BP的最小值，如图所示，当AP与BP共线时，AP+BP为最小.请你解决问题：当0＜x＜4时，则代数式 的最小值是（ ）
A、4 B、5 C、6 D、75. 如图所示，已知△ABC中，AB＝6，AC＝9，AD⊥BC于D，M为AD上任一点，则MC2-MB2等于（ ）
A、9 B、35 C、45 D、无法计算6. 如图，有一个绳索拉直的木马秋千，绳索AB的长度为5米.若将它往水平方向向前推进3米（即DE=3米），且绳索保持拉直的状态，则此时木马上升的高度为（ ）
A、1米 B、米 C、2米 D、4米7. 如图，长方体的高为 ， 底面是边长为的正方形一只蚂蚁从顶点开始爬向顶点 ， 那么它爬行的最短路程为（ ）
A、 B、 C、 D、8. 有一个边长为1的正方形，以它的一条边为斜边，向外作一个直角三角形，再分别以直角三角形的两条直角边为边，向外各作一个正方形，称为第一次“生长”（如图1）；再分别以这两个正方形的边为斜边，向外各自作一个直角三角形，然后分别以这两个直角三角形的直角边为边，向外各作一个正方形，称为第二次“生长”（如图2）……如果继续“生长”下去，它将变得“枝繁叶茂”，请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是（ ）
A、1 B、2020 C、2021 D、20229. 如图，某超市为了吸引顾客，在超市门口离地高4.5m的墙上，装有一个由传感器控制的门铃A，如①图所示，人只要移至该门铃5m及5m以内时，门铃就会自动发出语音“欢迎光临”.如②图所示，一个身高1.5m的学生走到D处，门铃恰好自动响起，则BD的长为（ ）
A、3米 B、4米 C、5米 D、7米10. 汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝．如图所示的弦图中，四个直角三角形都是全等的，它们的斜边长为5，较短直角边长为3，则图中小正方形（空白区域）的面积为（ ）
A、1 B、4 C、6 D、9二、填空题
-
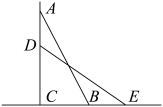
11. 如图，一架梯子AB长5米，底端离墙的距离BC为3米，当梯子下滑到DE时，米，则BE＝米.
12. 如图，在离水面高度为8米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为17米，几分钟后船到达点D的位置，此时绳子CD的长为10米，问船向岸边移动了米.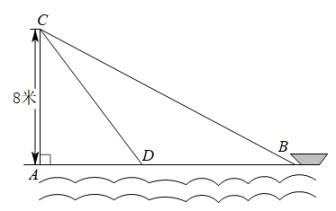
13. 如图，△ABC是直角三角形，所有的四边形都是正方形，其中最大的正方形的边长为9cm， 则正方形I，Ⅱ的面积之和为cm2 ．
14. 如图，用三张大小各不相同的正方形纸片以顶点相连的方式可以设计成“毕达哥拉斯”图案．现有四张大小各不相同的正方形纸片，其面积分别是1，2，3，4．若选取其中三张，按如图方式组成“毕达哥拉斯”图案，则所围成的Rt△ABC的斜边长可为 ．
15. 我国古代《九章算术》中的“折竹抵地问题”：一根竹子高一丈，折断后竹子顶端落在离竹子底端6尺处，折断处离地面的高度为尺．（一丈=10尺）三、综合题
-
16. 如图，在笔直的公路AB旁有一座山，为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处，已知点C与公路上的停靠站A的距离为15km，与公路上另一停靠站B的距离为20km，停靠站A、B之间的距离为25km，且CD⊥AB ．
(1)、求修建的公路CD的长；(2)、若公路CD修通后，一辆货车从C处经过D点到B处的路程是多少？17. 如图，在Rt△ABC中， ， ， 动点P从B出发沿射线以1 cm/s的速度运动，设运动时间为t（s）.
(1)、求边的长.(2)、当为等腰三角形时，求t的值.18. 如图，5米长的一根木棒AB靠在墙上A点处，落地点为B，已知OB＝4米．现从O点处拉出一根铁丝OP（点P在线段AB上）来加固该木棒
(1)、在图中画出铁丝最短时的情形，并求出此时铁丝的长度(2)、如果落地点B向墙角O处移动2米，则木棒上端A上移是少于2米，还是多于2米？并说明理由
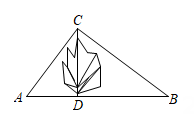
19. 如图，花果山上有两只猴子在一棵树上的点处， 且 ， 它们都要到处吃东西， 其中一只猴子甲沿树爬下走到离树处的池塘处， 另一只猴子乙先爬到树顶处后再沿缆绳线段滑到处.已知两只猴子所经过的路程相等，设为 ．
(1)、请用含有的整式表示线段的长为；(2)、求这棵树高有多少m？20. 伊通河，是长春平原上的千年古流，是松花江的二级支流，它发源于吉林省伊通县境内哈达岭山脉青顶山北麓，如图，在伊通河笔直的河流一侧有一旅游地 ， 河边有两个景点 、其中 ， 由于某种原因，由到的路现在已经不通，为方便游客决定在河边新建一个景点H（、、三点在同一直线上），并新修一条路 ， 测得千米，千米，千米．
(1)、判断的形状，并说明理由；(2)、求原路线的长．