2023年浙教版数学七年级上册2.6 有理数的混合运算同步测试（培优版）

试卷更新日期：2023-08-03 类型：同步测试

进入出卷网下载

一、选择题

1. 九宫格起源于中国古代的神秘图案河图和洛书.如图，将 $3$ ， $2$ ， $1$ ， $0$ ， $- 1$ ， $- 2$ ， $- 3$ ， $- 4$ ， $- 5$ 填入九宫格内，使每行、每列、每条对角线上三个数的和都相等，则 $a$ 的值为（）

A、 $- 2$ B、 $- 3$ C、 $- 4$ D、 $- 5$

查看试题解析
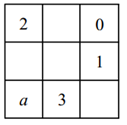2. 如图，已知正方形的边长为24厘米，甲，乙两动点分别从正方形ABCD的顶点D，B同时沿正方形的边开始移动，甲点按顺时针方向环行，乙点按逆时针方向环行，若乙的速度为9厘米/秒，甲的速度为3厘米/秒，当它们运动了2022秒时，它们在正方形边上相遇了（）

A、252 次 B、253次 C、254次 D、255次

查看试题解析
3. 济青高铁北线，共设有11个不同站点，要保证每两个站点之间都有高铁可乘，需要印制不同的火车票（）

A、110种 B、132种 C、55种 D、66种

查看试题解析

4. 计算机中常用的十六进制是逢16进1的计数制，采用数字0~9和字母A~F共16个计数符号，这些符号与十进制的数的对应关系如下表：

十六进制	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
十进制	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

例如，十进制中 $26 = 16 + 10$ ，用十六进制表示为1A：用十六进制表示： $D + F = 1 C$ ， $19 - F = A$ ，则 $A \times E$ ，用 $A \times E$ 十六进制可表示为（）

A、8C B、140 C、32 D、EO

查看试题解析

5. $2021$ 减去它的 $\frac{1}{2}$ ，再减去余下的 $\frac{1}{3}$ ，再减去余下的 $\frac{1}{4}$ ，....，以此类推，一直减到余下的 $\frac{1}{2021}$ ，则最后剩下的数是（）

A、 $0$ B、 $1$ C、 $\frac{2020}{2021}$ D、 $\frac{2021}{2020}$

查看试题解析
6. 水池 $A, B, C$ 都是长方体，深为 $1.6 m$ ，底部尺寸为 $3 m \times 4 m$ .1号阀门 $24 min$ 可将无水A池注满；2号阀门用来从A池向B池放水， $30 min$ 可将A池中满池水放入B池；3号阀门用来从B池向C池放水， $48 \min$ 可将B池中满池水放入C池.若开始 $A 、 B 、 C$ 三池无水，同时打开1号、2号和3号阀门，那么当B池水深 $0.4 m$ 时，A池有（） $m^{3}$ 的水.

A、1.2 B、3.2 C、6 D、16

查看试题解析
7. 如果有4个不同的正整数 $a$ 、 $b$ 、 $c$ 、 $d$ 满足 $(2019 - a) (2019 - b) (2019 - c) (2019 - d) = 9$ ，那么 $a + b + c + d$ 的值为（）

A、0 B、9 C、8076 D、8090

查看试题解析
8. 我们常用的数是十进制数，而计算机程序处理数据使用的只有数码0和1的二进制数，这二者可以相互换算，如将二进制数1011换算成十进制数应为：1×2³+0×2²+1×2¹+1×2⁰=11．按此方式，则将十进制数7换算成二进制数应为（）

A、101 B、110 C、111 D、1101

查看试题解析
9. 我国古代《易经》一书中记载：远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”.如图所示，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数.由图可知，孩子自出生后的天数是（）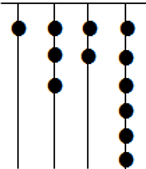

A、84 B、336 C、510 D、1326

查看试题解析
10. 已知 $a = 4 \times 10^{6} - {(- 2016)}^{2} ， b = {(- 40)}^{2} - 1016$ ， $c = 666^{2} - 666 \times 665$ ，则 $a ， b ， c$ 的大小关系是(　　)

A、 $a > b > c$ B、 $c > a > b$ C、 $b > c > a$ D、 $c > b > a$

查看试题解析

二、填空题

11. 已知整数a，b，c，且 $c < 0$ ，满足 $| a | + 10 b^{2} - 100 c^{3} = 2023$ ，则 $a + b + c$ 的最小值为.

查看试题解析
12. 设三个互不相等的有理数，既可表示为1、a+b、a的形式，又可表示为4、 $\frac{a}{b}$ 、b的形式，则（b-a）³的值为．

查看试题解析
13. 已知整数 $a$ ， $b$ ， $c$ ， $d$ 满足 $a b c d = 6$ ，且 $a > b > c > d$ ，则 ${(a + 3 c)}^{2020} - {(3 b + d)}^{2021}$ 的值为.

查看试题解析

14. 计算机中常用的十六进制是逢16进1的计数制，采用数字0~9和字母A~F共16个计数符号，这些符号与十进制的数的对应关系如下表：

十六进制	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
十进制	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

例如，十进制中16+10=26，用十六进制表示为10+A=1A；十进制中25-15=10，用十六进制表示为19−F=A．由上可知，在十六进制中B×D=（运算结果用十六进制表示）．

查看试题解析

15. 中百超市推出如下优惠方案：
⑴一次性购物不超过 100 元，不享受优惠
⑵一次性购物超过 100 元，但不超过 300 元一律 9 折；
⑶一次性购物超过 300 元一律 8 折．某人两次购物分别付款 80 元、252 元，如果他将这两次所购商品一次性购买，则应付款．

查看试题解析
16. 为冲刺即将到来的2020年全面建成小康社会，小全同学在黑板上写有1，2，3，…，2019，2020这2020个自然数，而小康同学对它们进行了操作，每次操作规则如下：擦掉写在黑板上的三个数后，再添写上所擦掉三个数之和的个位数字.例如：擦掉7，13和1998后，添上8；若再擦掉8，6，38，添上2，等等.如果经过1009次操作后，发现黑板上剩下两个数，一个是2019，则另一个数是.

查看试题解析

三、计算题

17. 不进行通分，计算：
$(1 + \frac{1}{12} + \frac{1}{13} + \frac{1}{14}) \times (\frac{1}{12} + \frac{1}{13} + \frac{1}{14} + \frac{1}{15}) - (1 + \frac{1}{12} + \frac{1}{13} + \frac{1}{14} + \frac{1}{15}) \times (\frac{1}{12} + \frac{1}{13} + \frac{1}{14})$ ．

查看试题解析
18. 请先阅读下列一段内容，然后解答问题：
因为： $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ，…… ， $\frac{1}{9 \times 10} = \frac{1}{9} - \frac{1}{10}$ ，

所以： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{9 \times 10}$

$= (1 - \frac{1}{2}) + (\frac{1}{2} - \frac{1}{3}) + (\frac{1}{3} - \frac{1}{4}) + \dots + (\frac{1}{9} - \frac{1}{10})$

$= 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \dots + \frac{1}{9} - \frac{1}{10} = 1 - \frac{1}{10} = \frac{9}{10}$

计算：

(1)、 $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{2007 \times 2008}$ ；

(2)、 $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \dots + \frac{1}{49 \times 51}$ .

查看试题解析
19. 观察 $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ =（1－ $\frac{1}{2}$ ）+（ $\frac{1}{2}$ － $\frac{1}{3}$ ）=1－ $\frac{1}{3}$ = $\frac{2}{3}$

(1)、计算： $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +……+ $\frac{1}{2013 \times 2014}$ =

(2)、计算： $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \dots \dots + \frac{1}{99 \times 101}$

查看试题解析

四、综合题

20. 某超市对顾客实行优惠购物，规定如下：
（1）若一次性购物不超过100元，则不予优惠；
（2）若一次性购物超过100元，但不超过300元，按标价给予九折优惠；
（3）若一次性购物超过300元，其中300元以下部分（包括300元）给予九折优惠；超过300元部分给予八折优惠.
小李两次去该超市购物，分别付款99元和252元.现在小张决定一次性购买小李分两次购买的物品，他需付款多少元?

查看试题解析
21. 今年以来，由于受国际天然气形势的影响，我国天然气市场总体呈现量紧价高的态势，为确保天然气保供稳价，提高居民生活用气的保障，某地决定从今年 $11$ 月开始调整居民用气价格，调整前后价格如下表（每月用气量为 $a$ 立方米）：

用气类别

第一档（ $0 < a \leq 60$ ）
第二档（ $60 < a \leq 80$ ）
第三档（ $a > 80$ ）
调整前
$2.60$
$2.90$
$3.65$
调整后
$2.95$
$3.25$
$4.10$
注：该地天然气收费按月实行阶梯收费

(1)、某用户 $10$ 月（调整前）缴天然气费 $91$ 元，求该用户这月用气量；

(2)、若该用户 $11$ 月（调整后）用气量与 $10$ 月相同，则该用户 $11$ 月比 $10$ 月多缴费多少元？

(3)、因天气转冷，该用户今年 $12$ 月因取暖用气量急剧增加，缴天然气费 $283$ 元，该用户今年 $12$ 月用气量是多少立方米？

查看试题解析
22. 有个补充运算符号的游戏：在“1□2□ $(- 6)$ □9”中的每个□内，填入+、-、×、÷中的某一个（可重复使用），然后计算结果．

(1)、计算： $1 + 2 - (- 6) - 9 =$ （直接写出结果）；

(2)、若 $1 \div 2 \times (- 6)$ □ $9 = 6$ ，请推算□内的符号应是什么？

(3)、请在□内填上×、÷中的一个，使计算更加简便，然后计算 $(1 \frac{3}{4} + \frac{7}{8} - \frac{7}{12})$ □ $(- \frac{7}{8})$

查看试题解析
23. 找规律并计算：

(1)、计算： $2^{2} - 1^{2}$ = ， $(2 + 1) (2 - 1)$ =；
$5^{2} - 2^{2}$ = ， $(5 + 2) (5 - 2)$ =；

(2)、猜想：观察上述式子可猜想出的结论是： $x^{2} - y^{2}$ =；

(3)、试用你所猜想的结论计算：
$2022^{2} - 2021^{2} + 2020^{2} - 2019^{2} +$ …… $+ 4^{2} - 3^{2} + 2^{2} - 1^{2}$ .

查看试题解析
24. 在抗洪抢险中，解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民，早晨从A地出发，晚上到达B地，约定向东为正方向，当天的航行路程记录如下（单位：千米）： $+ 14 ， - 9 ， + 8 ， - 7 ， + 13 ， - 6 ， + 12 ， - 5$

(1)、请你帮忙确定B地位于A地的什么方向，距离A地多少千米？

(2)、若冲锋舟每千米耗油 $0.5$ 升，油箱容量为28升，求冲锋舟当天救灾过程中至少还需补充多少升油？

(3)、救灾过程中，冲锋舟离出发点A最远处有多远？

查看试题解析
25. 规定：求若干个相同的不为零的有理数的除法运算叫做除方．如 $2 \div 2 \div 2$ ， $(- 3) ÷ (- 3) ÷ (- 3) ÷ (- 3)$ ．
类比有理数的乘方，我们把 $2 \div 2 \div 2$ 记作 $2^{★ 3 ★}$ ，读作“2的星3次方”；把 $(- 3) ÷ (- 3) ÷ (- 3) ÷ (- 3)$ 记作 $(- 3)^{★ 4 ★}$ ，读作“ $- 3$ 的星4次方”．
一般地，把 $\underset{n 个 a}{\underset{︸}{a \div a \div \dots \dots \div a}}$ 记作 $a^{★ n ★}$ （其中， $a \neq 0$ ， $n ⩾ 3$ ， $n$ 为整数），读作“ $a$ 的星 $n$ 次方”．

(1)、直接写出计算结果： $2^{★ 3 ★} =$ ， $(- 3)^{★ 4 ★} =$ ， $(- \frac{1}{4})^{★ 5 ★} =$ ；

(2)、结合（1）中的运算，尝试把有理数的除方运算转化为乘方运算，可以归纳如下：
一个非零有理数的星 $n (n \geq 3$ ， $n$ 为整数）次方等于（从以下四个选项中选择最合适的一个，填写序号即可）．
①这个数的相反数的 $(n - 2)$ 次方；
②这个数的绝对值的 $(n - 2)$ 次方；
③这个数的倒数的 $(n - 2)$ 次方；
④这个数的 $(n - 2)$ 次方．

(3)、关于“除方”运算，下列说法错误的是____ ；

A、任何非零有理数的星3次方都等于它的倒数； B、对于任何不小于3正整数 $n$ ， $1^{★ n ★} = 1$ ； C、 $4^{★ 5 ★} = 5^{★ 4 ★}$ ； D、负数的星5次方的结果是负数，负数的星6次方的结果是正数．

(4)、结合上述探究结果，计算下式的值．
$2 \times (- \frac{1}{2})^{★ 5 ★} - (- 3)^{★ 3 ★} \div \frac{1}{3}$ ．

查看试题解析

	用气类别
	第一档（ $0 < a \leq 60$ ）	第二档（ $60 < a \leq 80$ ）	第三档（ $a > 80$ ）
调整前	$2.60$	$2.90$	$3.65$
调整后	$2.95$	$3.25$	$4.10$

2023年浙教版数学七年级上册2.6 有理数的混合运算 同步测试（培优版）

一、选择题

二、填空题

三、计算题

四、综合题

2023年浙教版数学七年级上册2.6 有理数的混合运算同步测试（培优版）