2023-2024学年北师大版数学八年级上册1.2一定是直角三角形吗 同步练习（提升卷）

试卷更新日期：2023-08-02 类型：同步测试

进入 出卷网 下载

一、选择题

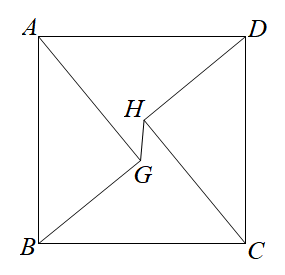
  • 1. 将直角三角形的三条边长做如下变化，得到的新三角形仍是直角三角形的是（    ）
    A、同加一个相同的数 B、同减一个相同的数 C、同乘以一个相同的正整数 D、同时平方

    查看试题解析

  • 2. 如图，正方形ABCD的边长为10，AG=CH=8，BG=DH=6，则线段GH的长为（    ）

    A、22 B、10−52 C、145 D、835

    查看试题解析

  • 3. △ABC的三条边分别为a，b，c，下列条件不能判断△ABC是直角三角形的是（    ）
    A、a2＋b2＝c2 B、∠A＝∠B＋∠C C、∠A∶∠B∶∠C＝3∶4∶5 D、a＝5，b＝12，c＝13

    查看试题解析

  • 4. 以下列数据为三角形的三边长，能构成直角三角形的是（    ）
    A、1，3 ， 4 B、35 ， 45 ， 1 C、32 ， 42 ， 52 D、6，7，8

    查看试题解析

  • 5. 下列各组数据中的三个数，可作为三边长构成直角三角形的是（   ）
    A、1、2、3 B、7、8、9 C、6、8、10 D、5、12、20

    查看试题解析

  • 6. 如图，在边长为1的正方形方格中，A，B，C，D均为格点，构成图中三条线段AB ， BC ， CD.现在取出这三条线段AB ， BC ， CD首尾相连拼三角形.下列判断正确的是（ ）

    A、能拼成一个锐角三角形 B、能拼成一个直角三角形 C、能拼成一个钝角三角形 D、不能拼成三角形

    查看试题解析

  • 7. 下列条件：①∠A+∠B=∠C；②a2=(b+c)(b−c)；③AB：BC：AC=3：4：5；④∠A：∠B：∠C=3：4：5 ， 其中不能确定△ABC是直角三角形的是（ ）
    A、① B、② C、③ D、④

    查看试题解析

  • 8. 满足下列条件的△ABC ， 不是直角三角形的是（    ）
    A、∠C=∠A−∠B B、a：b：c=5：12：13 C、∠A：∠B：∠C=3：4：5 D、b2−c2=a2

    查看试题解析

  • 9. 下列各组长度的线段，可以作为直角三角形三条边的是（    ）
    A、1cm、3cm和4cm B、9cm、12cm和15cm C、6cm、8cm和9cm D、4cm、6cm和45cm

    查看试题解析

  • 10. 五根小棒的长度（单位：cm）分别为7，15，20，24，25，现从中选择三根，将它们首尾相接摆成三角形，其中能摆成直角三角形的是（   ）
    A、7，15，20 B、7，20，24 C、15，20，25 D、20，24，25

    查看试题解析

二、填空题

  • 11. 已知一个三角形的三边长分别是4cm、7cm、6cm，该三角形的形状（填“是”或“不是”）直角三角形．

    查看试题解析

  • 12. 下列条件：①∠C＝∠A－∠B；②∠A：∠B：∠C＝5∶2∶3；③a＝35c，b＝45c；④a∶b∶c＝1∶2：3 ， 则能确定△ABC是直角三角形的条件有个．

    查看试题解析

  • 13. 如图，BD是△ABC的角平分线，AB=15 ， BC=9 ， AC=12 ， 则BD的长为 ．

    查看试题解析

  • 14. 在△ABC中，若AC2＋BC2＝AB2 ， ∠A∶∠B＝1∶2，则∠B的度数是.

    查看试题解析

  • 15. 杜老师要画一个三角形，画好后量得三边长分别为7cm，24cm和25cm，则这个三角形（填“是”或“不是”）直角三角形．

    查看试题解析

三、综合题

  • 16. 定义：如图，点M，N把线段AB分割成AM，MN，NB，若以AM，MN，NB为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．

    (1)、已知M，N把线段AB分割成AM，MN，NB，若AM= 1，MN=2，BN=3 ， 则点M，N是线段AB的勾股分割点吗？请说明理由．
    (2)、已知点M，N是线段AB的勾股分割点，且AM为直角边，若AB=12，AM=5，求BN的长．

    查看试题解析

  • 17. 如图，在△ABC中，AB=12 ， AC=16BC=20.

    (1)、判断△ABC的形状，并说明理由；
    (2)、若点P为线段A C上一点，连接BP，且BP=CP，求AP的长.

    查看试题解析

  • 18. 如图，某住宅小区在施工过程中留下了一块空地，已知AD=4米，CD=3米，∠ADC=90° ， AB=13米，BC=12米，小区为美化环境，欲在空地上铺草坪.

    (1)、△ABC是直角三角形吗？为什么？
    (2)、小区为美化环境，欲在空地上铺草坪，已知草坪每平方米100元，试问铺满这块空地共需花费多少元？

    查看试题解析

  • 19. 在一条东西走向河的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝AC，由于某种原因，由C到A的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点H（A、H、B在同一条直线上），并新修一条路CH，测得CB＝2.5千米，CH＝2千米，HB＝1.5千米．

    (1)、问CH是否为从村庄C到河边的最近路？请通过计算加以说明；
    (2)、求原来的路线AC的长．（精确到0.01）

    查看试题解析

  • 20. 已知，在长方形ABCD中，AB＝8，BC＝6，点E，F分别是边AB，BC上的点，连接DE，DF，EF．

    (1)、如图①，当CF＝2BE＝2时，试说明△DEF是直角三角形；
    (2)、如图②，若点E是边AB的中点，DE平分∠ADF，求BF的长．

    查看试题解析