2023-2024学年北师大版数学八年级上册1.1探索勾股定理 同步练习（培优卷）
试卷更新日期：2023-08-02 类型：同步测试
一、选择题
-
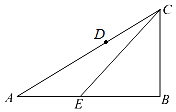
1. 如图，在Rt△ABC中，点D，E分别是边AC、AB上的两点，连接BD，CE，CD＝AE，已知BC＝6，AB＝8，则BD+CE的最小值是（ ）
A、 B、10 C、9.6 D、5+2. 如图，凸四边形 中， ，若点M、N分别为边 上的动点，则 的周长最小值为（ ）
A、 B、 C、6 D、33. 如图，已知 中， ， ，在BC边上取一点P（点P不与点B、C重合），使得 成为等腰三角形，则这样的点P共有（ ）.
A、1个 B、2个 C、3个 D、4个4. 已知等腰三角形 ， ，点 是 上一点，若 ， .则 的周长可能是（ ）A、15 B、20 C、28 D、365. 直角三角形纸片的两直角边长分别为6，8，现将 如图折叠，使点A和点B重合，则折痕DE的长是（ ）
A、3 B、3.5 C、3.75 D、46. 如图1，以直角三角形的各边为边分别向外作正三角形，再把较小的两张正三角形纸片按图2的方式放置在最大正三角形内．若知道图中阴影部分的面积，则一定能求出（ ）
A、直角三角形的面积 B、较小两个正三角重叠部分的面积 C、最大正三角形的面积 D、最大正三角形与直角三角形的面积差7. 如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长为（ ）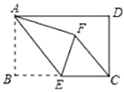
A、 B、 C、 D、8. 如图，等边△ABC的边长为2，AD是BC边上的中线，M是AD上的动点，E是边AC的中点，则EM+CM的最小值为（ ）
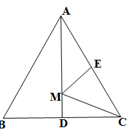A、1 B、2 C、3 D、9. 如图，等边△ABC的边长为6，AD是BC边上的中线，M是AD上的动点，E是边AC上一点，若AE=2，则EM+CM的最小值为（ ）
A、 B、 C、 D、10. 如图，在边长为1正方形ABCD中，E、F、G、H分别是AB、BC、CD、DA上的点，3AE=EB，有一只蚂蚁从E点出发，经过F、G、H，最后回点E点，则蚂蚁所走的最小路程是（ ）
A、2 B、4 C、 D、二、填空题
-
11. 如图，在中， ， 为边的中点，、分别为边、上的点，且 ， 若 ， ， 则 ， 线段的长度 ．
12. 等边△ABC的边长为2，过点C作直线lAB ， P为直线l上一点，且 ， 则点P到BC所在直线的距离是.13. 在△ABC中，BC=6，高线AD=4，则△ABC周长的最小值为 ．14. 如图，已知等边△ABC的边长为4，点P是边BC上一点，CP＝3，则AP＝ ， 若点Q是边AC上一点，BQ＝AP，则AQ＝.
15. 在Rt△ABC中，∠ABC=90°，AB=3，BC=4，点E，F分别在边AB，AC上，将△AEF沿直线EF翻折，点A落在点P处，且点P在直线BC上.则线段CP长的取值范围是.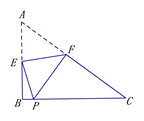
三、解答题
-
16. 如图，△ABC中，∠ACB＝90°，AB＝10，BC＝6，若点P从点A出发，以每秒1个单位长度的速度沿折线A－C－B－A运动，设运动时间为t秒（t＞0）．
(1)、若点P在AC上，且满足PA＝PB时，求此时t的值；(2)、若点P恰好在∠BAC的平分线上，求t的值．17. 如图，已知AB＝12，AB⊥BC于B，AB⊥AD于A，AD＝5，BC＝10点E是CD的中点，求AE的长．
18. 一个25米长的梯子AB，斜靠在一竖直的墙AO上，这时的AO距离为24米，如果梯子的顶端A沿墙下滑4米，那么梯子底端B也外移4米，对吗？为什么？
19. 在△ABC中，∠BAC=90°，AB=AC.点D为直线BC上一动点（点D不与点B、C重合），以AD为直角边在AD右侧作等腰直角三角形ADE，使∠DAE=90°，连结CE.
(1)、探究：如图①，当点D在线段BC上时，证明BC=CE+CD.
(2)、应用：在探究的条件下，若AB= ，CD=1，则△DCE的周长为.(3)、拓展：①如图②，当点D在线段CB的延长线上时，BC、CD、CE之间的数量关系为.②如图③，当点D在线段BC的延长线上时，BC、CD、CE之间的数量关系为.
20.
(1)、【证明体验】如图1，在中，为边上的中线，延长至E，使 ， 连接.求证：.(2)、【迁移应用】如图2，在中， ， ， 为的中点，.求面积.
(3)、【拓展延伸】如图3，在中， ， 是延长线上一点， ， F是上一点，连接交于点E，若 ， ， 求的长.