2023-2024学年北师大版数学八年级上册1.1探索勾股定理同步练习（提升卷）

试卷更新日期：2023-08-02 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在△ABC中，AB＝AC＝10，BC＝12，AD平分∠BAC，则AD等于（　　）

A、6 B、7 C、8 D、9

查看试题解析
2. 如图，在直线l上有正方形a，b，c，若a，c的面积分别为4和16，则b的面积为（）

A、24 B、20 C、12 D、22

查看试题解析
3. 在等腰 $△ A B C$ 中， $A B = A C = 5$ ， $B C = 2 \sqrt{13}$ ，则底边上的高为（）

A、12 B、 $2 \sqrt{3}$ C、 $3 \sqrt{2}$ D、18

查看试题解析
4. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ， $B D ⊥ A C$ 于点D，E是 $A C$ 上一点，且 $D E = D A$ ，若 $A B = 15$ ， $B C = 20$ ，则 $E C$ 的长为（）

A、 $6$ B、 $7$ C、 $8$ D、 $9$

查看试题解析
5. 如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长是 $9 c m$ ，则图中所有正方形的面积的和是（）

A、 $64 c m^{2}$ B、 $81 c m^{2}$ C、 $162 c m^{2}$ D、 $243 c m^{2}$

查看试题解析
6. 如图，四个全等的直角三角形和中间的小正方形可以拼成一个大正方形，若直角三角形的较长直角边长为a，较短直角边长为b，大正方形面积为S₁ ，小正方形面积为S₂ ，则（a+b）²可表示为（）

A、S₁-S₂ B、2S₁-S₂ C、S₁+S₂ D、S₁+2S₂

查看试题解析
7. 如图，在四边形ABCD中，∠DAB＝∠BCD＝90°，分别以四边形ABCD的四条边为边向外作四个正方形，面积分别为S₁ ， S₂ ， S₃ ， S₄ ．若S₁＝48，S₂+S₃＝135，则S₄＝（）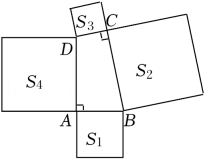

A、183 B、87 C、119 D、81

查看试题解析
8. 如果将长为6cm，宽为5cm的长方形纸片折叠一次，那么这条折痕的长不可能是（）

A、7cm B、5cm C、5.5cm D、8cm

查看试题解析
9. 如图，在边长为1个单位长度的小正方形组成的网格中，点 $A$ ， $B$ 都是格点，则线段 $A B$ 的长为（）

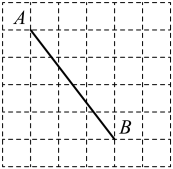A、4 B、5 C、6 D、7

查看试题解析
10. 如图，已知钓鱼竿 $A C$ 的长为 $10 m$ ，露在水面上的鱼线 $B C$ 长为 $6 m$ ，某钓鱼者想看看鱼钩上的情况，把鱼竿 $A C$ 转动到 $A C^{'}$ 的位置，此时露在水面上的鱼线 $B^{'} C^{'}$ 为 $8 m$ ，则 $B B^{'}$ 的长为（）

A、 $1 m$ B、 $2 m$ C、 $3 m$ D、 $4 m$

查看试题解析

二、填空题

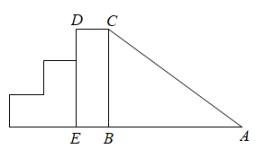
11. 如图是一个滑梯示意图，左边是楼梯，右边是滑道，已知滑道 $A C$ 与 $A E$ 的长度相等，滑梯的高度 $B C = 6 m$ ， $B E = 2 m$ .则滑道 $A C$ 的长度为m.

查看试题解析
12. 如图，有一张直角三角形的纸片， $∠ A C B = 90 ° ， A B = 5 ， A C = 3$ .现将三角形折叠，使得边 $A C$ 与 $A B$ 重合，折痕为 $A E$ .则 $C E$ 长为.

查看试题解析
13. 如图所示的正方形网格中，每一个小正方形的面积均为1，正方形 $A B C M$ ， $C D E N$ ， $M N P Q$ 的顶点都在格点上，则正方形 $M N P Q$ 的面积为．

查看试题解析
14. 如图，有一张直角三角形纸片，两直角边AC＝4cm，BC＝8cm，将△ABC折叠，使点B与点A重合，折痕为DE，则CD的长是．

查看试题解析
15. 清代数学家梅文鼎在《勾股举隅》一书中，用四个全等的直角三角形拼出正方形ABCD的方法证明了勾股定理（如图）．连结CE，若 $C E = 5$ ， $B E = 4$ ，则正方形ABCD的边长为．

查看试题解析

三、解答题

16. 如图， $△ A B C$ 是张大爷的一块小菜地，已知CD是 $△ A B C$ 中AB边上的高， $A C = 5 ， C D = 4 ， B C = 3 A D$ ，求BD的长．（结果保留根号）

查看试题解析
17. 如图，已知在Rt△ABC中，∠ACB＝90°，AC＝9，BC＝12，AB的垂直平分线交AB于点D，交BC于点E，连结AE，求BE的长.

查看试题解析
18. 如图，在四边形 $A B C D$ 中， $∠ B = ∠ C = 90 ° ， A B = A D = 24 c m ， B C = 16 c m ， C D = 8 c m$ ，E为 $B C$ 上一点．将四边形沿 $A E$ 折叠，使点 $B ， D$ 重合，求折痕 $A E$ 的长．

查看试题解析
19. 如图，在△ABC中，AD平分∠BAC.AB=AC=3，AD=2，求BC的长.

查看试题解析
20. 如图，在Rt△ABC中，∠B=90°，AB=4，BC=3，阴影部分是一个长方形，AE=1，求阴影部分的面积．

查看试题解析

2023-2024学年北师大版数学八年级上册1.1探索勾股定理 同步练习（提升卷）

一、选择题

二、填空题

三、解答题

2023-2024学年北师大版数学八年级上册1.1探索勾股定理同步练习（提升卷）