北师大版数学九年级上册同步练习——第六章《反比例函数》综合练习A
试卷更新日期:2023-08-02 类型:单元试卷
一、选择题(每题3分,共36分)
-
1. 从1,2,3这三个数中随机抽取两个不同的数,分别记作和.若点的坐标记作 , 则点在双曲线上的概率是( )A、 B、 C、 D、2. 已知压力、压强与受力面积之间有如下关系式: . 当F为定值时,下图中大致表示压强p与受力面积S之间函数关系的是( )A、
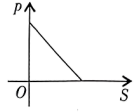 B、
B、 C、
C、 D、
D、 3. 正在建设中的临滕高速是我省“十四五”重点建设项目.一段工程施工需要运送土石方总量为 , 设土石方日平均运送量为V(单位:/天),完成运送任务所需要的时间为t(单位:天),则V与t满足( )A、反比例函数关系 B、正比例函数关系 C、一次函数关系 D、二次函数关系4. 若点是反比例函数图象上一点,则常数的值为( )A、3 B、 C、 D、5. 反比例函数(为常数,)的图象位于( )A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限6. 如图,在函数 的图象上任取一点A,过点A作y轴的垂线交函数 的图象于点B,连接OA,OB,则 的面积是( )
3. 正在建设中的临滕高速是我省“十四五”重点建设项目.一段工程施工需要运送土石方总量为 , 设土石方日平均运送量为V(单位:/天),完成运送任务所需要的时间为t(单位:天),则V与t满足( )A、反比例函数关系 B、正比例函数关系 C、一次函数关系 D、二次函数关系4. 若点是反比例函数图象上一点,则常数的值为( )A、3 B、 C、 D、5. 反比例函数(为常数,)的图象位于( )A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限6. 如图,在函数 的图象上任取一点A,过点A作y轴的垂线交函数 的图象于点B,连接OA,OB,则 的面积是( )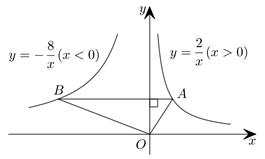 A、3 B、5 C、6 D、107. 如图,一次函数与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为 , 则不等式的解集是( )
A、3 B、5 C、6 D、107. 如图,一次函数与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为 , 则不等式的解集是( )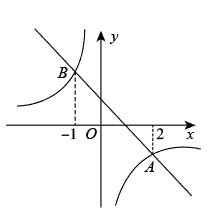 A、或 B、或 C、或 D、8. 若反比例函数的图象过点 , 则该图象必经过第( )象限A、一、三 B、二、四 C、一、二 D、三、四9. 对于反比例函数 , 下列说法不正确的是( )A、点在它的图象上 B、它的图象在第二、四象限 C、当时,随的增大而增大 D、当时,随的增大而减小10. 已知反比例函数的图象过点 , 则代数式的值为( )A、 B、2 C、 D、11. 对于函数 , 下列说法错误的是( )A、它的图像分布在第一、三象限 B、它的图像与直线无交点 C、当时,y的值随x的增大而增大 D、当时,y的值随x的增大而减小12. 如图,点A是反比例函数的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
A、或 B、或 C、或 D、8. 若反比例函数的图象过点 , 则该图象必经过第( )象限A、一、三 B、二、四 C、一、二 D、三、四9. 对于反比例函数 , 下列说法不正确的是( )A、点在它的图象上 B、它的图象在第二、四象限 C、当时,随的增大而增大 D、当时,随的增大而减小10. 已知反比例函数的图象过点 , 则代数式的值为( )A、 B、2 C、 D、11. 对于函数 , 下列说法错误的是( )A、它的图像分布在第一、三象限 B、它的图像与直线无交点 C、当时,y的值随x的增大而增大 D、当时,y的值随x的增大而减小12. 如图,点A是反比例函数的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( ) A、3 B、-6 C、6 D、-3
A、3 B、-6 C、6 D、-3二、填空题(每空3分,共18分)
-
13. 如图,在平面直角坐标系中,点在反比例函数为常数, , 的图象上,过点作轴的垂线,垂足为 , 连接 . 若的面积为 , 则 .
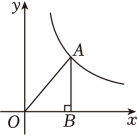 14. 科技小组为了验证某电路的电压U(V)、电流I(A)、电阻 三者之间的关系: ,测得数据如下:
14. 科技小组为了验证某电路的电压U(V)、电流I(A)、电阻 三者之间的关系: ,测得数据如下:100
200
220
400
2.2
1.1
1
0.55
那么,当电阻 时,电流 A.
15. 如图,点P(x,y)在双曲线的图象上,PA⊥x轴,垂足为A,若S△AOP=2,则该反比例函数的解析式为 .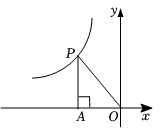 16. 已知一个反比例函数的图象经过点 ,若该反比例函数的图象也经过点 ,则 .17. 如图,在平面直角坐标系中,一次函数y=x+b的图象与反比例函数的图象交于 A(1,y1)B(-3,y2).请根据图象写出不等式的解集 .
16. 已知一个反比例函数的图象经过点 ,若该反比例函数的图象也经过点 ,则 .17. 如图,在平面直角坐标系中,一次函数y=x+b的图象与反比例函数的图象交于 A(1,y1)B(-3,y2).请根据图象写出不等式的解集 . 18. 如图,等边△ABO的顶点O与原点重合,点A的坐标是(-4,0),点B在第二象限.反比例函数的图象经过点B,则k的值是 .
18. 如图,等边△ABO的顶点O与原点重合,点A的坐标是(-4,0),点B在第二象限.反比例函数的图象经过点B,则k的值是 .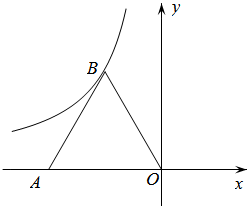
三、解答题(共7题,共66分)
-
19. 如图,一次函数与反比例函数的图象交于 , 两点.
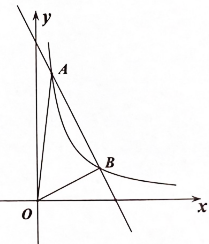 (1)、求反比例函数的表达式.(2)、根据图象,直接写出时的取值范围.20. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m)的反比例函数,其图象如图所示.
(1)、求反比例函数的表达式.(2)、根据图象,直接写出时的取值范围.20. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m)的反比例函数,其图象如图所示. (1)、求这个函数的表达式;(2)、当气球的体积是1m3时,气球内的气压是多少千帕?21. 如图,在平面直角坐标系xOy中,点A和点B在x轴的负半轴上, , , 以线段AB为边向上作正方形ABCD,反比例函数的图象经过顶点C,且与边AD相交于点E.
(1)、求这个函数的表达式;(2)、当气球的体积是1m3时,气球内的气压是多少千帕?21. 如图,在平面直角坐标系xOy中,点A和点B在x轴的负半轴上, , , 以线段AB为边向上作正方形ABCD,反比例函数的图象经过顶点C,且与边AD相交于点E. (1)、当时,求k的值及点E的坐标;(2)、连接OC,CE,OE.
(1)、当时,求k的值及点E的坐标;(2)、连接OC,CE,OE.①若的面积为 , 求该反比例函数的表达式;
②是否存在某一位置,使得 . 若存在,请求出m的值;若不存在,请说明理由.
22. 如图,在平面直角坐标系中,一次函数y=k1x+b的图像与反比例函数 的图像交于A(4,﹣2)、B(﹣2,n)两点,与x轴交于点C. (1)、求k2 , n的值;(2)、请直接写出不等式k1x+b< 的解集;(3)、将x轴下方的图像沿x轴翻折,点A落在点A′处,连接A′B、A′C,求△A′BC的面积.23. 如图,反比例函数的图象与一次函数的图象交于点 , .
(1)、求k2 , n的值;(2)、请直接写出不等式k1x+b< 的解集;(3)、将x轴下方的图像沿x轴翻折,点A落在点A′处,连接A′B、A′C,求△A′BC的面积.23. 如图,反比例函数的图象与一次函数的图象交于点 , .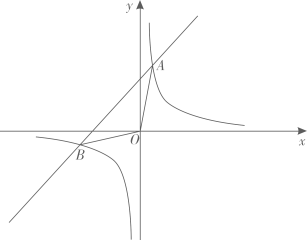 (1)、若 , 求与的值;(2)、关于的不等式的解集为;(3)、连接 , , 若的面积为12,则的值为.24. 如图,在平面直角坐标系中,一次函数与反比例函数交于 , 两点,与y轴交于点C,连接 , .
(1)、若 , 求与的值;(2)、关于的不等式的解集为;(3)、连接 , , 若的面积为12,则的值为.24. 如图,在平面直角坐标系中,一次函数与反比例函数交于 , 两点,与y轴交于点C,连接 , .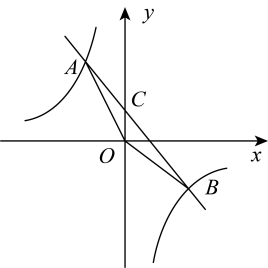 (1)、求反比例函数和一次函数的表达式;(2)、求的面积;(3)、请根据图象直接写出不等式的解集.25. 在实验课上,小明做了一个试验.如图,在仪器左边托盘(固定)中放置一个物体,在右边托盘(可左右移动)中放置一个可以装水的容器,容器的质量为 . 在容器中加入一定质量的水,可以使仪器左右平衡.改变托盘与点的距离()(),记录容器中加入的水的质量,得到下表:
(1)、求反比例函数和一次函数的表达式;(2)、求的面积;(3)、请根据图象直接写出不等式的解集.25. 在实验课上,小明做了一个试验.如图,在仪器左边托盘(固定)中放置一个物体,在右边托盘(可左右移动)中放置一个可以装水的容器,容器的质量为 . 在容器中加入一定质量的水,可以使仪器左右平衡.改变托盘与点的距离()(),记录容器中加入的水的质量,得到下表:
托盘与点的距离
30
25
20
15
10
容器与水的总质量
10
12
15
20
30
加入的水的质量
5
7
10
15
25
把上表中的与各组对应值作为点的坐标,在平面直角坐标系中描出这些点,并用光滑的曲线连接起来,得到如图所示的关于的函数图象.
 (1)、请在该平面直角坐标系中作出关于的函数图象;(2)、观察函数图象,并结合表中的数据:
(1)、请在该平面直角坐标系中作出关于的函数图象;(2)、观察函数图象,并结合表中的数据:①猜测与之间的函数关系,并求关于的函数表达式;
②求关于的函数表达式;
③当时,随的增大而(填“增大”或“减小”),随的增大而(填“增大”或“减小”),的图象可以由的图象向(以“上”或“下”或“左”或“右”)平移得到.
(3)、若在容器中加入的水的质量(g)满足 , 求托盘与点的距离(cm)的取值范围.