2023-2024学年初中数学八年级上册 17.5 反证法同步分层训练基础卷(冀教版)

试卷更新日期：2023-08-02 类型：同步测试

进入出卷网下载

一、选择题

1. 用反证法证明“若 $x^{2} \neq y^{2}$ ，则 $x \neq y$ ”时，应首先假设（）

A、 $x > y$ B、 $x = y$ C、 $x < y$ D、 $| x | = | y |$

查看试题解析
2. 用反证法证明“在 $△ A B C$ 中，若 $A B = A C$ ，则 $∠ B < 90 °$ ”时，以下三个步骤正确的排列顺序是（）
步骤如下：
①假设在△ABC中，∠B≥90° .
②因此假设不成立，：∴∠B<90°.
③由AB=AC，得∠B=∠C≥90°，即∠B+∠C≥180°，∴∠A+∠B+∠C> 180°，这与“三角形三个内角的和等于180°”产生矛盾.

A、①③② B、①②③ C、③①② D、③②①

查看试题解析
3. 用反证法证明命题“三角形中至少有一个内角大于或等于 $6 0^{°}$ ”时，首先应假设这个三角形中（）

A、每一个内角都大于 $6 0^{°}$ B、每一个内角都小于 $6 0^{°}$ C、有一个内角大于 $6 0^{°}$ D、有一个内角小于 $6 0^{°}$

查看试题解析
4. 用反证法证明“一个三角形中最多有一个角为直角”时，应先作出的假设是（）

A、一个三角形中至少有两个角为直角 B、一个三角形中没有一个角为直角 C、一个三角形中至少有两个角为锐角 D、一个三角形中至少有两个角为钝角

查看试题解析
5. 用反证法证明“在 $△ A B C$ 中，若 $A B = A C$ ，则 $∠ B = ∠ C$ ”时，则应假设（）

A、 $∠ A = ∠ B$ B、 $∠ B \neq ∠ C$ C、 $A B \neq A C$ D、 $B C = A C$

查看试题解析
6. 我们可以用以下推理来证明“在一个三角形中，至少有一个内角小于或等于 $60 °$ ”．假设三角形没有一个内角小于或等于 $60 °$ ，即三个内角都大于 $60 °$ ．则三角形的三个内角的和大于 $180 °$ ，这与“三角形的内角和等于 $180 °$ ”这个定理矛盾．所以在一个三角形中，至少有一个内角小于或等于 $60 °$ ．上述推理使用的证明方法是（）

A、反证法 B、比较法 C、综合法 D、分析法

查看试题解析
7. 下列说法，错误的是（）

A、一个三角形两边的垂直平分线的交点到这个三角形三个顶点的距离相等 B、“若 $a > b$ ，则 $a^{2} > b^{2}$ ”的逆命题是假命题 C、在角的内部到角的两边距离相等的点一定在这个角的平分线上 D、用反证法证明“三角形中必有一个角不大于 $60 °$ ”，先假设这个三角形中有一个内角大于60°

查看试题解析
8. 用反证法证明“在同一平面内，有三条直线a，b，c，若 $\vec{a} ⊥ \vec{b}$ ， $c ⊥ b$ ，则 $a ∥ c$ ”时，应先假设（）

A、 $c ∥ b$ B、 $a ∥ b$ C、 $a$ 与 $c$ 相交 D、 $a$ 与 $b$ 相交

查看试题解析

二、填空题

9. 把下列命题补充完整，使之成为真命题：“在同一平面内的三条直线a，b，c，若 $a ⊥ b$ ， $b ∥ c$ ，则． ”

查看试题解析
10. 阅读下列材料：“为什么 $\sqrt{2}$ 不是有理数”，完成问题.
证明：假设 $\sqrt{2}$ 是有理数，

那么存在两个互质的正整数 $p$ 、 $q$ ，使得 $\sqrt{2} = \frac{p}{q}$ ，于是 $p = \sqrt{2} q$ ，

∴      ▲

∵ $2 q^{2}$ 是偶数，可得 $p^{2}$ 是偶数.

∵只有偶数的平方才是偶数，∴ $p$ 也是偶数.

∴可设 $p = 2 s$ ，代入，得      ▲      .可得      ▲

∴      ▲      .这样， $p$ 和 $q$ 都是偶数，不互质，这与假设 $p$ ， $q$ 互质矛盾.

这个矛盾说明， $\sqrt{2}$ 不能写成分数的形式，即 $\sqrt{2}$ 不是有理数.

将下列选项依次填入材料中的画线处，正确的顺序是.（填上序号）

① $4 s^{2} = 2 q^{2}$ ；    ② $p^{2} = 2 q^{2}$ ；    ③ $q$ 是偶数；    ④ $q^{2} = 2 s^{2}$ .

查看试题解析
11. 用反证法证明：一个三角形中至少有一个角不小于60°，应先假设．

查看试题解析
12. 用反证法证明命题“在一个三角形中，不能有两个内角为钝角”时，第一步应假设．

查看试题解析
13. 用反证法证明“三角形的三个内角中至多有一个钝角”时，应假设．

查看试题解析

三、解答题

14. 用反证法证明：一个三角形中不能有两个角是直角．
已知： $∠ A$ ， $∠ B$ ， $∠ C$ 是 $△ A B C$ 的三个内角．
求证： $∠ A$ ， $∠ B$ ， $∠ C$ 中不能有两个角是直角．

查看试题解析
15. 阅读材料：怎样证实“两直线平行，同位角相等”
本节中，我们用叠合的方法发现了“两直线平行，同位角相等” .事实上，这个结论可以运用已有的基本事实，通过说理加以证实.
如图，直线AB、CD被直线EF所截，AB//CD，∠1与∠2是同位角.
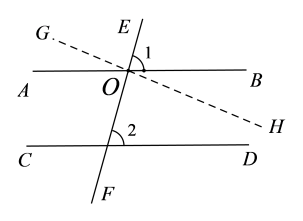
假设∠1 $\neq$ ∠2，那么可以通过直线AB与EF的交点O作直线GH，使∠EOH=∠2，直线GH与直线AB是两条直线.
根据基本事实“同位角相等，两直线平行”，由∠EOH=∠2，可以得到GH//CD.
这样，过点O就有两条直线AB、GH都与CD平行.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”矛盾.
这说明∠1 $\neq$ ∠2的假设不正确，于是∠1=∠2.
解决问题：若 $x \neq 0$ 且 $y \neq 0$ ，请你用以上方法说明： $x^{2} + y^{2} \neq {(x + y)}^{2}$ .

查看试题解析

四、综合题

16. 人教版初中数学教科书七年级下册第18－19页告诉我们平行线所具有的3个性质：
性质1：两条平行线被第三条直线所截，同位角相等.

简单说成：两直线平行，同位角相等.

其中性质2、3都是利用性质1推导出来的，但是书上却没给出性质1的推理过程，而是通过测量观察数据而得出的.九年级上册学习了反证法后，我们可以尝试给出证明了.

已知：直线AB//CD，直线EF分别交AB、CD于点G、H，求证：∠BGF＝∠DHF.

证明：假设（1），

过点G作直线PQ，使得∠PGF＝∠DHF，

∴PQ//CD（（2）），

∵AB//CD，且AB也过点G，

∴与（（3））矛盾，

所以假设错误，即∠BGF＝∠DHF.

请完成上面（1）、（2）、（3）空：

(1)、；

(2)、；

(3)、请选择合理的依据（）

A、两点确定一条直线 B、两直线平行，同位角相等 C、经过直线外一点，有且只有一条直线与这条直线平行 D、如果两条直线都与第三条直线平行，那么这两条直线也互相平行

查看试题解析
17. 如果10^b=n，那么b为n的劳格数，记为b=d（n），由定义可知：10^b=n与b=d（n）所表示的b、n两个量之间的同一关系．

(1)、根据劳格数的定义，填空：d（10）= ， d（10^﹣²）=；

(2)、劳格数有如下运算性质：
若m、n为正数，则d（mn）=d（m）+d（n），d（ $\frac{m}{n}$ ）=d（m）﹣d（n）．
根据运算性质，填空：
$\frac{d (a^{3})}{d (a)}$ =（a为正数），若d（2）=0.3010，则d（4）= ， d（5）= ， d（0.08）=；

(3)、如表中与数x对应的劳格数d（x）有且只有两个是错误的，请找出错误的劳格数，说明理由并改正．
x
1.5
3
5
6
8
9
12
27
d（x）
3a﹣b+c
2a﹣b
a+c
1+a﹣b﹣c
3﹣3a﹣3c
4a﹣2b
3﹣b﹣2c
6a﹣3b

查看试题解析

x	1.5	3	5	6	8	9	12	27
d（x）	3a﹣b+c	2a﹣b	a+c	1+a﹣b﹣c	3﹣3a﹣3c	4a﹣2b	3﹣b﹣2c	6a﹣3b

2023-2024学年初中数学八年级上册 17.5 反证法 同步分层训练基础卷(冀教版)

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学八年级上册 17.5 反证法同步分层训练基础卷(冀教版)