2023-2024学年初中数学八年级上册 17.2 直角三角形 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-02 类型:同步测试
一、选择题
-
1. 如图所示,在中,于于 , 点是的中点,的周长是10,则是( )
 A、 B、 C、 D、182. 如图,在中, , 点为斜边上的中点,则为( )
A、 B、 C、 D、182. 如图,在中, , 点为斜边上的中点,则为( ) A、10 B、3 C、5 D、43. 下面是“作已知直角三角形的外接圆”的尺规作图过程:
A、10 B、3 C、5 D、43. 下面是“作已知直角三角形的外接圆”的尺规作图过程:已知:如图1,在中, .
求作:的外接圆.
作法:如图2.
(1)分别以点A和点B为圆心,大于的长为半径作弧,两弧相交于P,Q两点;
(2)作直线 , 交于点O;
(3)以O为圆心,为半径作 , 即为所求作的圆.
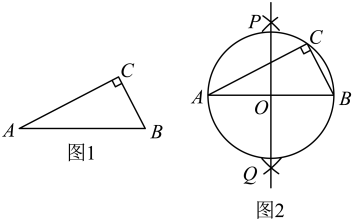
下列不属于该尺规作图依据的是( )
A、两点确定一条直线 B、直角三角形斜边上的中线等于斜边的一半 C、与线段两个端点距离相等的点在这条线段的垂直平分线上 D、线段垂直平分线上的点与这条线段两个端点的距离相等4. 一副直角三角板按如图所示的方式放置,点E在边BC的延长线上, , , 则的度数为( ) A、30° B、25° C、20° D、15°5. 如图,在中, , 点在边上,点在内部,且是等边三角形, . 若 , , 则的面积为( )
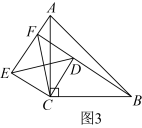
A、30° B、25° C、20° D、15°5. 如图,在中, , 点在边上,点在内部,且是等边三角形, . 若 , , 则的面积为( ) A、 B、 C、 D、6. 如图,等腰中, , , 于点 , 的平分线分别交、于、两点,为的中点,的延长线交于点 , 连接 , 下列结论:;为等腰三角形;;; , 其中正确结论有( )
A、 B、 C、 D、6. 如图,等腰中, , , 于点 , 的平分线分别交、于、两点,为的中点,的延长线交于点 , 连接 , 下列结论:;为等腰三角形;;; , 其中正确结论有( )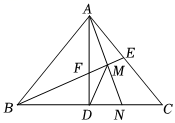 A、2个 B、3个 C、4个 D、5个7. 如图,∠MON=90°,OB=4,点A是直线OM上的一个动点,连结AB,作∠MAB与∠ABN的角平分线AF与BF,两条角平分线所在的直线相交于点F,则点A在运动过程中线段BF的最小值为( )
A、2个 B、3个 C、4个 D、5个7. 如图,∠MON=90°,OB=4,点A是直线OM上的一个动点,连结AB,作∠MAB与∠ABN的角平分线AF与BF,两条角平分线所在的直线相交于点F,则点A在运动过程中线段BF的最小值为( ) A、4 B、 C、8 D、28. 如图,在Rt△ABC中,∠ABC=90°,AB=BC,点P在△ABC内一点,连接PA,PB,PC,若∠BAP=∠CBP,且AP = 6,则PC的最小值是( )
A、4 B、 C、8 D、28. 如图,在Rt△ABC中,∠ABC=90°,AB=BC,点P在△ABC内一点,连接PA,PB,PC,若∠BAP=∠CBP,且AP = 6,则PC的最小值是( )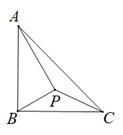 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,小虎用块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板 , 点在上,点和分别与木墙的顶端重合,则两堵木墙之间的距离为 .
 10. 如图,在中, , , , 平分 , 于点 , 则的周长是 .
10. 如图,在中, , , , 平分 , 于点 , 则的周长是 . 11. 如图,将放在正方形网格图中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,那么的度数是.
11. 如图,将放在正方形网格图中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,那么的度数是. 12. 如图, , 均为等腰直角三角形, , , 若四边形的面积为 , 的面积为 , 则与的数量关系为 .
12. 如图, , 均为等腰直角三角形, , , 若四边形的面积为 , 的面积为 , 则与的数量关系为 . 13. 已知等腰 , , .现将以点B为旋转中心旋转45°,得到 , 延长交直线于点D.则的长度为.
13. 已知等腰 , , .现将以点B为旋转中心旋转45°,得到 , 延长交直线于点D.则的长度为.三、解答题
-
14. 如图1,放在墙角的立柜的上下底面是等腰直角三角形,如图2所示,若腰长为1m,现要将这个立柜搬过宽为0.8m的通道,你觉得能通过吗?请说明理由.
 15. 如图,已知在中, , 是的高,点E在边上,与交于点F,且 , 试说明 .
15. 如图,已知在中, , 是的高,点E在边上,与交于点F,且 , 试说明 .
解:∵是的高(已知)
∴(垂直的意义)
∵ ,
∴∠▲
∴ .
在和中
(请继续完成以下说理过程)
四、综合题
-
16. 在等腰中, , 点是射线上的动点,垂直于直线于点 , 交直线于点 .
 (1)、【探索发现】如图①,若点在的延长线上,点在线段上时,请猜想 , , 之间的数量关系为;(2)、【拓展提升】如图②,若点在线段上(不与点 , 重合),试猜想 , , 之间的数量关系,并说明理由:(3)、【灵活应用】当 , 时,直接写出线段的长为17. 已知等腰中, , 点D在射线上,连接 , 在右侧作等腰 , 且
(1)、【探索发现】如图①,若点在的延长线上,点在线段上时,请猜想 , , 之间的数量关系为;(2)、【拓展提升】如图②,若点在线段上(不与点 , 重合),试猜想 , , 之间的数量关系,并说明理由:(3)、【灵活应用】当 , 时,直接写出线段的长为17. 已知等腰中, , 点D在射线上,连接 , 在右侧作等腰 , 且 (1)、如图1,若平分 , 延长、交于点F,求证:;(2)、如图2,点M为的中点,求证:点M在线段的垂直平分线上;(3)、如图3,射线与射线交于点G,若 , 求的度数.18. 某校一数学兴趣小组在一次合作探究活动中,将两块大小不同的等腰直角三角形和等腰直角三角形 , 按如图1的方式摆放, . 该数学兴趣小组进行如下探究,请你帮忙解答:(1)、【初步探究】如图1,试探究与的位置关系,并说明理由;
(1)、如图1,若平分 , 延长、交于点F,求证:;(2)、如图2,点M为的中点,求证:点M在线段的垂直平分线上;(3)、如图3,射线与射线交于点G,若 , 求的度数.18. 某校一数学兴趣小组在一次合作探究活动中,将两块大小不同的等腰直角三角形和等腰直角三角形 , 按如图1的方式摆放, . 该数学兴趣小组进行如下探究,请你帮忙解答:(1)、【初步探究】如图1,试探究与的位置关系,并说明理由; (2)、【深入探究】如图2,当、、三点共线时,请探究此位置时线段、、之间的数量关系,并说明理由;
(2)、【深入探究】如图2,当、、三点共线时,请探究此位置时线段、、之间的数量关系,并说明理由; (3)、【拓展延伸】如图3,当、、三点不共线时,连接 , 延长交于点 , 连接 , 请猜想此位置时线段、、之间的数量关系: .
(3)、【拓展延伸】如图3,当、、三点不共线时,连接 , 延长交于点 , 连接 , 请猜想此位置时线段、、之间的数量关系: .