2023-2024学年初中数学八年级上册 16.2 线段的垂直平分线 同步分层训练培优卷(冀教版)
试卷更新日期：2023-08-02 类型：同步测试
一、选择题
-
1. 把各顶点的横坐标都乘以-1，纵坐标都不变，所得图形是下列答案中的（ ）A、
B、
C、
D、
2. 在一些美术字中，有的汉字是轴对称图形.下面4个汉字中，可以看作是轴对称图形的是（ ）A、共 B、力 C、齐 D、心3. 下列数学符号中，属于轴对称图形的是（ ）A、 B、> C、 D、4. 在下列交通标志中，是轴对称图形的是（ ）A、
B、
C、
D、
5. 甲骨文是中国的一种古代文字，是汉字的早期形式，有时候也被认为是汉字的书体之一，也是现存中国王朝时期最古老的一种成熟文字．下图为甲骨文对照表中的四个字，若把这四个甲骨文的文字抽象为几何图形，其中最接近轴对称图形的是（ ）A、
B、
C、
D、
6. 下面这些钢架雪车运动标志中是轴对称图形的是（ ）A、
B、
C、
D、
7. 如图，在四边形 ABCD 中，∠C=70°，∠B=∠D=90°，E、F 分别是 BC、DC 上的点，当△AEF 的周长最小时，∠EAF 的度数为（ ）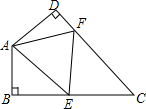
A、30° B、40° C、50° D、70°8. 如图， ，点B关于 的对称点E恰好落在 上，若 ，则 的度数为（ ）
A、45° B、 C、 D、二、填空题
-
9. 如图，四边形ABCD是轴对称图形，直线AC是它的对称轴，若 ， 则的大小为 ．
10. 如图是一个轴对称图形，若 ， 则 ．
11. 如图，桌球的桌面上有M，N两个球，若要将M球射向桌面的一边，反弹一次后击中N球，则A，B，C，D，4个点中，可以反弹击中N球的是点.
12. 如图的4×4的正方形网格中，△ABC的顶点都在小正方形的格点上，这样的三角形称 为格点三角形，在网格中与△ABC全等的格点三角形一共有个．
13. 如图，在 的正方形格纸中，有一个以格点为顶点的 ，请你找出格纸中所有与 成轴对称且也以格点为顶点的三角形，这样的三角形共有个.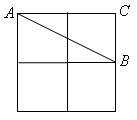
三、解答题
-
14. 在平面直角坐标系中的位置如图所示，A、B、C三点在格点上，点B的坐标为 ．
（ 1 ）作出 关于x轴对称的 ，并写出点 的坐标；
（ 2 ）作出 关于y轴对称的 ，并写出点 的坐标，
15. 如图，在平面直角坐标系中，△ABC的三个顶点分别为A（1，1），B（3，﹣3），C（4，3）．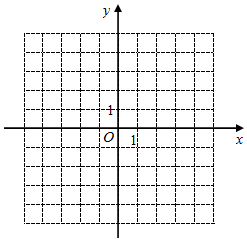
( 1 )在平面直角坐标系中标出A、B、C三点，画出△ABC；
( 2 )作出△ABC关于y轴的对称图形△A1B1C1 ， 并写出A1、B1、C1三点坐标．
四、作图题
-
16. 已知：如图，△AOB的顶点O在直线
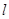上，且AO=AB. 
(1)、画出△AOB关于直线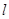 成轴对称的图形△COD，且使点A的对称点为点C； (2)、在(1)画出的图形中，AC与BD的位置关系是；(3)、在(1)画出的图形中连接AD，如果∠ABD=2∠ADB.求证：△AOC是等边三角形，并直接写出∠DAO∶∠DAB的值.
五、综合题
-
17. 如图1，△ABC是等腰直角三角形，∠ACB＝90°，AC＝BC.D是BC上任意一点（点D与点B，C都不重合），连接AD，CF⊥AD，交AD于点E，交AB于点F，BG⊥BC交CF的延长线于点G.
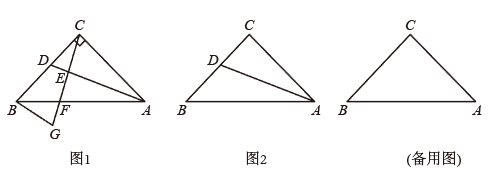(1)、写出与BG相等的线段，并证明.(2)、若点D为线段BC的中点，其余条件不变，连接DF.根据题意，先在图2中补全图形，再证明：∠BDF＝∠CDE.(3)、当点C和点F关于直线AD成轴对称时，直接写出线段CE，DE，AD三者之间的数量关系.18. 如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．
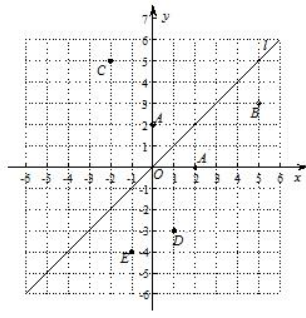(1)、实验与探究：
由图观察易知A（0，2）关于直线l的对称点A′的坐标为（2，0），请在图中分别标明B(5，3)、C(-2，5)关于直线l的对称点B′、C′的位置，并写出他们的坐标：B′、C′；(2)、归纳与发现：
结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(a，b)关于第一、三象限的角平分线l的对称点P′的坐标为（不必证明）；(3)、运用与发现：
已知两点D(1，-3)、E(-1，-4)，试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小.
-