2023-2024学年初中数学八年级上册 14.2 立方根同步分层训练培优卷(冀教版)

试卷更新日期：2023-08-02 类型：同步测试

进入出卷网下载

一、选择题

1. 下列说法正确的是（　　）

A、1的平方根是1 B、负数没有立方根 C、 $\sqrt{81}$ 的算术平方根是3 D、 ${(- 3)}^{2}$ 的平方根是 $- 3$

查看试题解析
2. 下列说法错误的是（）

A、两个无理数的和一定是无理数 B、 $\sqrt{81}$ 的平方根是 $\pm 3$ C、 ${(- 1)}^{2020}$ 是最小的正整数 D、实数与数轴上的点一一对应

查看试题解析
3. 下列式子正确的是（）

A、 $\sqrt[3]{- 7} = - \sqrt[3]{7}$ B、 $\sqrt{25} = \pm 5$ C、 $\pm \sqrt{49} = 7$ D、 $\sqrt{{(- 3)}^{2}} = - 3$

查看试题解析
4. 下列命题中，是真命题的是（）

A、立方根等于本身的数是0，1 B、两条直线被第三条直线所截，内错角相等 C、过一点有且只有一条直线与这条直线平行 D、在同一平面内，垂直于同一条直线的两条直线平行

查看试题解析
5. 有下列说法：① $- 1$ 的立方根是 $- 1$ ；②0的算术平方根是0；③ $- 5$ 是25的一个平方根；④ $\pm 2$ 是8的立方根；⑤81的平方根是9．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 下列命题：①立方根是它本身的数只有3个；② $\frac{1}{27}$ 的立方根是 $\frac{1}{3}$ 与 $- \frac{1}{3}$ ；③ $- 81$ 无立方根；④互为相反数的两个数的立方根也互为相反数；是真命题的是（）

A、①② B、①③ C、①④ D、②④

查看试题解析
7. 下列运算正确的是（）

A、 $\sqrt{8} = 4$ B、 $\sqrt[3]{64} = 4$ C、 $\sqrt{1 \frac{9}{16}} = 1 \frac{3}{4}$ D、 $\sqrt{36} = \pm 6$

查看试题解析
8. 下列说法正确的是（）

A、4的平方根是2 B、8的立方根是±2 C、如果一个数的立方根是这个数本身，那么这个数是-1，0或1 D、如果一个数的平方根是这个数本身，那么这个数是1或0

查看试题解析

二、填空题

9. 设实数x，y，z适合9x³=8y³=7z³ ， $\frac{9}{x} + \frac{8}{y} + \frac{7}{z} = 1$ ，则 $\sqrt[3]{{(9 x)}^{2} + {(8 y)}^{2} + {(7 z)}^{2}}$ =
$\sqrt[9]{{(9 x^{2})}^{4} + {(8 y^{2})}^{4} + {(7 z^{2})}^{4}}$ =

查看试题解析
10. 一个正方体的体积扩大为原来的27倍，则它的棱长变为原来的倍．

查看试题解析
11. 若a、b互为相反数，c为8的立方根，则 $2 a + 2 b - c =$ ．

查看试题解析
12. 36的算术平方根是， $- \frac{a}{125}$ 的立方根是．

查看试题解析
13. 数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：求59319的立方根．华罗庚脱口而出：39．众人感觉十分惊奇，请华罗庚给大家解读其中的奥秘．
你知道怎样迅速准确的计算出结果吗？请你按下面的问题试一试：

① 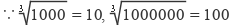，又，

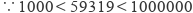，∴能确定59319的立方根是个两位数．

②∵59319的个位数是9，又，∴能确定59319的立方根的个位数是9．

③如果划去59319后面的三位319得到数59，

而，则，可得，

由此能确定59319的立方根的十位数是3

因此59319的立方根是39．

(1)、现在换一个数195112，按这种方法求立方根，请完成下列填空．
①它的立方根是位数．

②它的立方根的个位数是．

③它的立方根的十位数是．

④195112的立方根是．

(2)、请直接填写结果：
① ．

② ．

查看试题解析

三、计算题

14. 计算：（1） ${0.064}^{\frac{1}{3}} - 2 \sqrt{3} \times \sqrt[3]{1.5} \times \sqrt[6]{12}$

查看试题解析

四、解答题

15. 已知 $2 x + y + 17$ 的立方根是3，16的算术平方根是 $2 x - y + 2$ ，求： $x^{2} + y^{2}$ 的平方根．

查看试题解析
16. 已知2a﹣1的平方根是±3，3a+b+9的立方根是3，求2（a+b）的平方根．

查看试题解析

五、综合题

17. 据说我国著名数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：一个数是59319，希望求出它的立方根．华罗庚脱口而出：39．邻座的乘客十分惊奇，忙问计算的奥妙，华罗庚讲述了计算过程：
第一步：因为 $1 0^{3} = 1000$ ， $10 0^{3} = 1000000$ ， $1000 < 59319 < 1000000$ ，所以 $10 < \sqrt[3]{59319} < 100$ ．
第二步：因为59319的个位上的数是9，只有个位数字是9的数的立方的个位数字是9，所以 $\sqrt[3]{59319}$ 的个位数字是9．
第三步：如果划去59319后面的三位319得到数59，而 $3^{3} = 27$ ， $4^{3} = 64$ ，所以 $30 < \sqrt[3]{59000} < 40$ ，
所以 $30 < \sqrt[3]{59319} < 40$ ，即 $\sqrt[3]{59319}$ 的十位数字是3．
所以 $\sqrt[3]{59319} = 39$ ．
请根据上述材料解答下列问题：

(1)、用上述方法确定4913的立方根的个位数字是．

(2)、用上述方法确定50653的立方根是．

(3)、求 $\sqrt[3]{110592}$ 的值，要求写出计算过程．

查看试题解析
18. 期末复习过程中，七（1）班的张老师设计了一个数学问题，涉及本册中多个知识点和多种数学思想，请聪明的你来解答一下吧．

(1)、若一个数x的立方等于﹣8，请求出x的值．

(2)、请利用整体思想和方程思想进行解题．
①若（1）中的x的值也是关于x的一元一次方程 $\frac{1}{2}$ x﹣3＝5x﹣p的解，那么关于y的一元一次方程 $\frac{1}{2}$ （y﹣8）﹣3＝5（y﹣8）﹣p的解为y＝ ▲ ．

②在如图所示的“幻方”中，每个小三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等，现将①中的x，y填入如图所示的位置，则（a﹣b）+（d﹣c）的值为多少？

(3)、在（2）的条件下，在数轴上标注x，y所表示的数的对应点，分别记作A，B，已知P点从A点出发，以1个单位每秒的速度向B点运动，Q点从B点出发，以4个单位每秒的速度在A、B两点之间做往返运动，P、Q两点同时开始运动，当Q点第一次返回到B点时，两点同时停止运动，若记数轴的原点为O，则P点运动几秒后OQ＝2OP？

查看试题解析

2023-2024学年初中数学八年级上册 14.2 立方根 同步分层训练培优卷(冀教版)

一、选择题

二、填空题

三、计算题

四、解答题

五、综合题

2023-2024学年初中数学八年级上册 14.2 立方根同步分层训练培优卷(冀教版)