2023-2024学年初中数学八年级上册 13.4 三角形的尺规作图 同步分层训练培优卷(冀教版)
试卷更新日期:2023-08-02 类型:同步测试
一、选择题
-
1. 在下列各题中,属于尺规作图的是( )A、用直尺画一工件边缘的垂线 B、用直尺和三角板画平行线 C、利用三角板画 的角 D、用圆规在已知直线上截取一条线段等于已知线段2. 边长为1的正方形格点图中,点P为格点上一点,点M在正方形ABCD边上运动,点N在正方形EFGH边上运动,则△PMN的面积不可能是( )
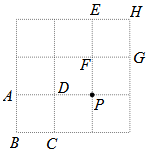 A、1 B、1.5 C、2 D、2.13. 如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC , 作图痕迹中,弧FG是( )
A、1 B、1.5 C、2 D、2.13. 如图,点C在∠AOB的边OB上,用尺规作出了∠BCN=∠AOC , 作图痕迹中,弧FG是( )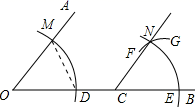 A、以点C为圆心,OD为半径的弧 B、以点C为圆心,DM为半径的弧 C、以点E为圆心,OD为半径的弧 D、以点E为圆心,DM为半径的弧4. 如图,已知钝角 ,依下列步骤尺规作图,并保留了作图痕迹.
A、以点C为圆心,OD为半径的弧 B、以点C为圆心,DM为半径的弧 C、以点E为圆心,OD为半径的弧 D、以点E为圆心,DM为半径的弧4. 如图,已知钝角 ,依下列步骤尺规作图,并保留了作图痕迹.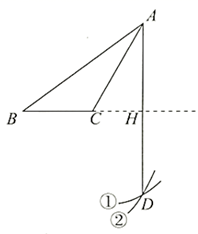
步骤1:以 为圆心, 长为半径画弧①;
步骤2:以 为圆心, 长为半径画弧②,交弧①于点 ;
步骤3:连接 ,交 的延长线于点 .
则下列说法错误的是( )
A、 是 中 边上的高 B、 C、 平分 D、作图依据是:①两点确定一条直线;②到线段两端点距离相等的点在线段的垂直平分线上5. 下面是教师出示的作图题.已知:线段 , ,小明用如图所示的方法作 ,使 , 上的高 .
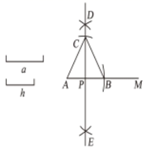
作法:①作射线 ,以点 为圆心、 ※ 为半径画弧,交射线 于点 ;②分别以点 , 为圆心、 △ 为半径画弧,两弧交于点 , ;③作直线 ,交 于点 ;④以点 为圆心、 为半径在 上方画孤,交直线 于点 ,连接 , .
对于横线上符号代表的内容,下列说法错误的是( )
A、※代表“线段a的长” B、△代表“任意长” C、△代表“大于 的长” D、 代表“线段 的长”6. 下面是黑板上出示的尺规作图题,需要回答横线上符号代表的内容.如图,已知∠AOB,求作:∠DEF,使∠DEF=∠AOB.
作法:
⑴以△为圆心,任意长为半径画弧,分别交OA,OB于点P,Q;
⑵作射线EG,并以点E为圆心,○长为半径画弧交EG于点D;
⑶以点D为圆心,* 长为半径画弧交前弧于点F;
⑷作⊕,则∠DEF即为所求作的角.
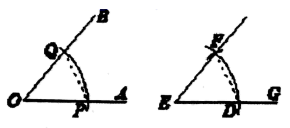 A、△表示点E B、○表示PQ C、*表示ED D、⊕表示射线EF7. 嘉淇在用直尺和圆规作一个角等于已知角的步骤如下:
A、△表示点E B、○表示PQ C、*表示ED D、⊕表示射线EF7. 嘉淇在用直尺和圆规作一个角等于已知角的步骤如下:已知:∠AOB .
求作:∠A'O'B',使∠A'O'B'=∠AOB .
作法:
⑴如图,以点O为圆心,m为半径画弧,分别交OA , OB于点C , D;
⑵画一条射线O'A',以点O'为圆心,n为半径画弧,交O'A'于点C';
⑶以点C'为圆心,p为半径画弧,与第(2)步中所画的弧相交于点D';
⑷过点D'画射线O'B',则∠A'O'B'=∠AOB .

下列说法正确的是( )
A、m-p>0 B、1-p>0 C、p= n>0 D、m=n>08. 如图,已知线段a、h,作等腰三角形 , 使 , 且 , 边上的高 . 张红的作法是:

⑴作线段;
⑵作线段的垂直平分线 , 与相交于点D;
⑶在直线上截取线段h;
⑷联结、 , 为所求的等腰三角形.
上述作法的四个步骤中,有不正确的一步你认为是( ).
A、(1) B、(2) C、(3) D、(4)二、填空题
-
9. 如图,∠EAD为锐角,C是射线AE上一点,点B在射线AD上运动(点A与点B不重合),设点C到AD的距离为d,BC长度为a,AC长度为b,在点B运动过程中,b、d保持不变,当a满足条件时,△ABC唯一确定.
 10. 请在由边长为1的小正三角形组成的虚线网格中,画一个所有顶点均在格点上,且至少有一条边为无理数的等腰三角形 .
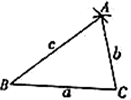
10. 请在由边长为1的小正三角形组成的虚线网格中,画一个所有顶点均在格点上,且至少有一条边为无理数的等腰三角形 . 11. 已知线段a,b,c,求作 ,使 , , ,下面作法的合理顺序为(填序号)
11. 已知线段a,b,c,求作 ,使 , , ,下面作法的合理顺序为(填序号)①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;
②作直线 ,在 上截取 ;
③连接 , , 为所求作的三角形.
 12. 利用尺规作三角形,有三种基本类型:
12. 利用尺规作三角形,有三种基本类型:⑴已知三角形的两边及其夹角,求作符合要求的三角形,其作图依据是“”;
⑵已知三角形的两角及其夹边,求作符合要求的三角形,其作图依据是“”;
⑶已知三角形的三边,求作符合要求的三角形,其作图依据是“”.
三、解答题
-
13. 已知:平行四边形ABCD ,
求作:矩形AECF , 使点E , F分别在边BC , AD上.

四、作图题
-
14. Rt△ABC中,∠A=90°,D点为AB边的中点
 (1)、如图1,连接CD,试判断S△ACD和S△BCD的大小关系,并说明理由.(2)、如图2,请利用尺规作图,在AB边上作出一点E,使得S△ABC= S△ACE(保留作图痕迹,不写作法).15. 在5×5的正方形网格中,每个小正方形的边长均为1,点A、B在网格格点上,若点C也在网格格点上,分别在下面的3个图中画出△ABC使其面积为2(形状完全相同算一种).
(1)、如图1,连接CD,试判断S△ACD和S△BCD的大小关系,并说明理由.(2)、如图2,请利用尺规作图,在AB边上作出一点E,使得S△ABC= S△ACE(保留作图痕迹,不写作法).15. 在5×5的正方形网格中,每个小正方形的边长均为1,点A、B在网格格点上,若点C也在网格格点上,分别在下面的3个图中画出△ABC使其面积为2(形状完全相同算一种).
五、综合题
-
16. 已知:在下列平面直角坐标系中,点A在y轴上,位于原点上方,距离原点3个单位长度;点C在x轴上,位于原点右侧,距离原点4个单位长度;点B坐标 ,
 (1)、在平面直角坐标系中分别描出A,B,C三个点,画出 .(2)、求的面积:(3)、已知点P在x轴上,以A,C,P为顶点的三角形面积为3,请直接写出P点的坐标.17. 在中,三个顶点的坐标分别为 , , ,
(1)、在平面直角坐标系中分别描出A,B,C三个点,画出 .(2)、求的面积:(3)、已知点P在x轴上,以A,C,P为顶点的三角形面积为3,请直接写出P点的坐标.17. 在中,三个顶点的坐标分别为 , , ,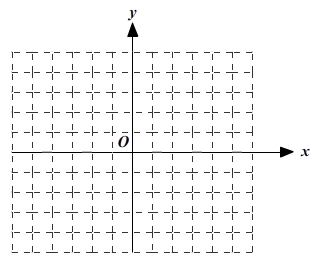 (1)、在直角坐标系描出、、三点.(2)、将沿轴负方向平移5个单位长度,再沿轴在正方向平移3个单位长度得到 , 求的三个顶点坐标.(3)、设点在坐标轴上,且与的面积相等,求点的坐标18. 如图
(1)、在直角坐标系描出、、三点.(2)、将沿轴负方向平移5个单位长度,再沿轴在正方向平移3个单位长度得到 , 求的三个顶点坐标.(3)、设点在坐标轴上,且与的面积相等,求点的坐标18. 如图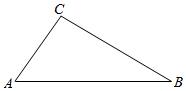 (1)、作图:如图,已知△ABC , ∠ACB<120°,
(1)、作图:如图,已知△ABC , ∠ACB<120°,①作等边△ACD , 使得点D , B分别是直线AC异侧的两个点;
②作等边△BCE , 使得点E , A分别是直线BC异侧的两个点;
(要求尺规作图,保留作图痕迹,不写作法.)
(2)、推理:在(1)所作的图中,设直线BD , AE的交点为P , 连接PC ,①求∠APD的度数;
②猜想PA , PB , PC与AE之间的等量关系,并证明:
(3)、变式:已知△ABC , ∠ACB>120°,按(1)的方法作图后,设直线BD , AE的交点为P , 连接PC . 测得∠PAB=15°,PA= ,PB= ,PC= .求点D到直线AB的距离.
-